Включение отечественных товаропроизводителей в международную торговлю и конкуренцию, внедрение в России международных стандартов управления качеством ИСО серии 9000 [3, 4, 5] привело к необходимости не только повышения качества продукции, но и документального подтверждения этого.
Вопросы управления качеством имели и имеют приоритетный характер. Несмотря на широкое внедрение методов менеджмента качества, статистических методов контроля и управления, до сих пор не удается найти универсальный подход, позволяющий подойти к бездефектному производству. Брак – это бич современной экономики.
Разумеется, разные виды продукции требуют разных систем и методов контроля и управления качеством.
В настоящее время предлагается использовать методы менеджмента качества, направленные на построение систем бездефектного производства. Это, однако, является недостижимым идеалом. Причина этого в том, что процесс возникновения брака носит вероятностный характер. В этой связи можно утверждать, что брак был, есть и будет. Вопрос только в том, как минимизировать возможные издержки.
В данной статье будут рассмотрены некоторые методы статистического приемочного контроля (СПК), которые в ряде случаев являются единственно возможным способом оценить качество изделий
Основная проблема, возникающая при проведении статистического приемочного контроля (СПК) партий продукции любого вида, заключается в том, что все существующие методы оценки качества партии на основе данных контроля случайной выборки основываются на распределении Пуассона числа дефектов, как в выборке, так и в партии. Необходимо заметить, что распределение Пуассона является не очень точным приближением биномиального распределения, которое, в свою очередь, при решении задач контроля является приближением точного гипергеометрического распределения.
Точное гипергеометрическое распределение при больших объемах партии практически невозможно вычислить, т.к. необходимо считать факториалы больших чисел.
Очевидно, что двойное приближение приводит к существенным ошибкам.
Ниже будет широко использоваться термин «план контроля». План контроля – это набор числовых параметров (объем выборки и приемочное число / числа) и регламента по выбору того или иного решения по результатам контроля. Под приемочным числом понимают максимально допустимое в выборке количество обнаруженных дефектов (дефектных или негодных к применению изделий), когда партия в целом может считаться удовлетворяющей требованиям Потребителя.
На ряде предприятий с крупносерийным производством до сих пор применяют старый стандарт ГОСТ 18242-72 [1]. Он имеет ряд недостатков. Во-первых, при расчете предлагаемых планов контроля использовалось распределение Пуассона числа дефектных изделий в выборке, что не дает возможность явно учесть объем контролируемой партии, а имеющиеся рекомендации носят эмпирический характер. Во-вторых, имеется большое количество планов контроля с нулевым приемочным числом, что не позволяет оценить реальное положение дел. В-третьих, планы контроля, предлагаемые стандартом, имеют высокий средний объем инспекции.
Эти недостатки объяснимы, если учесть невысокие возможности существовавшей в то время вычислительной техники и высокую стоимость проведения расчетов.
Современные персональные компьютеры обладают вычислительной мощностью, превосходящей любые суперкомпьютеры конца 60-х ‒ начала 70-х годов. Это позволяет кардинально изменить сам подход к выбору планов статистического приемочного контроля.
С точки зрения автора, вообще не должно существовать стандартов на выбор планов СПК. Каждое предприятие имеет свои характерные особенности, объем партий, предъявляемых к испытанию, может отличаться от того, что имеется в стандартах. Необходимо лишь регламентировать алгоритмы расчетов планов СПК и последующих оценок.
Автор предлагает следующий подход, основанный на математическом аппарате теории информации и концепции «интегрального риска».
Оперативная кривая информационного плана контроля
Принцип контроля по альтернативному признаку предполагает разбиение множества изделий на две группы: 1 – изделия годные; 2 – изделия бракованные. Пусть q – вероятность получения бракованного изделия. Процесс, характеризуемый двумя состояниями, вероятность нахождения в которых постоянна, а сумма этих вероятностей равна единице, есть биномиальный процесс, оценить который можно с помощью его энтропии
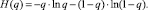
Функция H(q) является теоретическим параметром, характеризующим состояние процесса. Оценкой этого параметра является эмпирическая энтропия
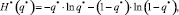
где q* = d/n; n – объем выборки, по которой оценивается качество потока; d – число дефектных изделий, обнаруженных в выборке.
Эмпирическая энтропия является состоятельной, смещенной и асимптотически нормальной оценкой энтропии [6], причем
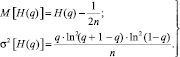 (1)
(1)
Пусть Ho = H(qo) – энтропия процесса, соответствующая допустимому входному уровню дефектности qo.
Оперативная кривая информационного плана контроля определяется следующим образом:
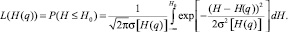 (2)
(2)
Оперативная кривая – это вероятность забраковать партию при заданной доле дефектных изделий в ней.
Зафиксируем объем выборки n. Введем понятие приемочного числа dп такого, что 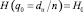 . Зададим также значения приемочной qп и браковочной qб дефектностей (долей брака), а также риски потребителя b и поставщика a. Так как
. Зададим также значения приемочной qп и браковочной qб дефектностей (долей брака), а также риски потребителя b и поставщика a. Так как
a = 1 – L(qп)
или
L(qп) = 1 – a,
а
L(qп) = Ф(to),
где
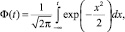
а
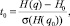
получаем, что
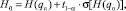
где t1–a – (1 – a)-квантиль нормального распределения.
Отсюда получаем уравнение, определяющее dп как неявную функцию объема выборки n:
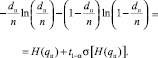 (3)
(3)
Браковочное число dб определяется аналогично из условия, что вероятность принятия партии при входной дефектности qб равна 1 – b.
Отсюда получаем
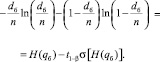 (4)
(4)
Планы контроля, полученные выше, рассчитываются, исходя из требований поставщика либо потребителя. Часто ставится задача удовлетворить обоим требованиям одновременно. В этом случае приемочное и браковочное числа рассматриваются как функции объема выборки n при фиксированных a, b, qп, qб.
Требуемый план контроля определяется совместным решением уравнений (3) и (4) с дополнительным условием dп = dб. Из этих уравнений с учетом вышесказанного получаем
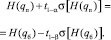 (5)
(5)
Решение уравнения (5) дает значение объема выборки n, при котором возможно удовлетворить требованиям поставщика и потребителя одновременно:
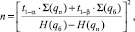 (6)
(6)
где 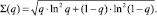
Искомое значение приемочного числа dп определяется из уравнения (3) при найденном из (6) значении объема выборки.
На рисунке приведен пример оперативной кривой информационного плана контроля и ее сравнение с оперативной кривой, рассчитанной на основе распределения Пуассона.
Можно заметить, что кривая информационного плана контроля существенно круче и ниже кривой пуассоновского плана, что уменьшает оба риска. Это подтверждено и результатами имитационного моделирования процесса контроля.
Информационные планы контроля, методика расчета которых приведена выше, имеют ряд преимуществ перед теми, которые рассчитаны на основе распределения Пуассона. Как показано в работе С.В. Юдина и других [6], средний объем инспекции у них ниже, объем выборки, как правило, также меньше, чем у планов СПК, предлагаемых стандартами. Тем не менее и у этого подхода имеются свои недостатки. В первую очередь следует отметить, что ни в одной методике нет учета индивидуальных особенностей предприятия. Кроме того, понятия риска Потребителя и Изготовителя (Поставщика) определяются точечно, в то время как любого участника контроля интересует в целом вероятность получения бракованной партии, т.е. такой, доля или количество дефектных изделий в которой превышает оговоренную величину.
Принцип интегрального риска в крупносерийном и массовом производстве
Для того чтобы ответить на этот вопрос, необходимо знать распределение дефектности изделий. Оно может быть получено на основе анализа данных о качестве продукции за достаточно большой промежуток времени. Эта информация носит объективный характер, в отличие от признака «уровень доверия».
Пусть плотность распределения доли дефектных изделий описывается функцией w(q). Пусть фиксированы объем выборки n и приемочное число c. Вероятность того, что доля брака в принятой партии будет выше оговоренной qб, равна
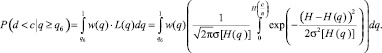 (7)
(7)
Эту вероятность назовем интегральным риском Потребителя.
В (7) и ниже d – количество дефектных изделий, обнаруженных в выборке.
Вероятность того, что в результате контроля будет забракована партия с дефектностью меньшей оговоренной, будет равна
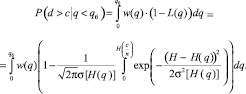 (8)
(8)
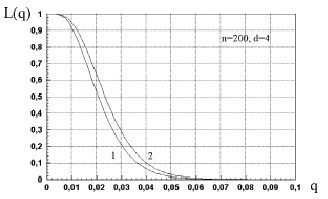
Пример оперативных кривых: 1 – информационный план контроля; 2 – пуассоновский план контроля
Эту вероятность назовем интегральным риском Производителя (Поставщика).
Данный подход позволяет, как видно из вышесказанного, учесть индивидуальные особенности предприятия, исключить из рассмотрения параметр «уровень доверия», более точно оценить реальные риски Потребителя и Поставщика.
Для определения плана контроля необходимо совместное решение системы уравнений (7) и (8) при заданном значении предельно допустимой дефектности партии qб, заданных рисках a, b, объеме партии N и функции плотности входной дефектности w(q) относительно объема выборки и приемочного числа.
Объем выборки плана контроля с использованием концепции интегрального риска позволяет снизить объем выборки в 8…10 раз.
Принцип интегрального риска при контроле малых партий
Проблема контроля малых партий заключается в том, что при высоком качестве (и, соответственно, низкой доле брака) объем выборки становится соизмерим с объемом партии, и, в ряде случаев, более целесообразно производить сплошной контроль, что существенно увеличивает себестоимость изделий. В то же время концепция «интегрального риска» позволяет уменьшить объем выборки и средний объем инспекции.
При контроле партий малого объема используется точное гипергеометрическое распределение числа дефектных изделий в выборке:
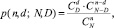 (9)
(9)
где n – объем выборки; d – количество дефектных изделий в выборке; N – объем партии; D – количество дефектных изделий в партии. Пусть с – приемочное число, тогда оперативная кривая плана контроля имеет вид
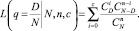 (10)
(10)
При традиционном подходе риск Изготовителя a определяется как вероятность забраковать партию с количеством дефектных изделий равных Dп:
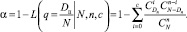 (11)
(11)
Риск Потребителя b определяется как вероятность принять партию с количеством дефектных изделий Dб:
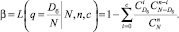 (12)
(12)
Здесь Dп и Dб – приемочное и браковочное количества дефектных изделий в партии (Dп < Dб).
Как правило, уровень качества на предприятии в среднем удовлетворяет самым жестким требованиям Потребителя, тем не менее планы контроля, рекомендуемые ГОСТ Р 50779.51-95 [2], имеют высокий риск Поставщика. Учет истории технологического предприятия дает возможность построить ряд распределения входного уровня дефектности (или количества дефектных изделий в партии при постоянном объеме). В этом случае возможно резкое снижение риска Поставщика за счет использования информации об истории качества и использования понятия интегрального риска.
Пусть заданы интегральные риски Потребителя b и Поставщика a. Тогда для определения объема выборки n и приемочного числа c имеем следующую систему неравенств:
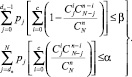 (13)
(13)
Здесь pj – вероятность появления j дефектов; dп – предельно допустимое количество дефектов в партии.
Выводы
Информационно-статистический подход к расчету планов статистического приемочного контроля позволяет повысить точность и надежность результатов контроля. Предложенная автором концепция интегрального риска дополнительно снижает средний объем инспекции и позволяет учесть историю работы предприятия.
Полученные результаты дают основание полагать, что их внедрение в практику позволит существенно снизить расходы на управление качеством.
Рецензенты:
Архипов И.К., д.т.н., профессор, Тульский филиал, Российская международная академия туризма, г. Тула;
Поляков В.А., д.э.н., доцент, заведующий кафедрой «Экономика, менеджмент и маркетинг», Тульский филиал, Финансовый университет при Правительстве Российской Федерации, г. Тула.
Библиографическая ссылка
Юдин С.В. НЕКОТОРЫЕ ПРОБЛЕМЫ СТАТИСТИЧЕСКОГО КОНТРОЛЯ КАЧЕСТВА И МЕТОДЫ ИХ РЕШЕНИЯ // Фундаментальные исследования. 2015. № 10-2. С. 324-329;URL: https://fundamental-research.ru/ru/article/view?id=39173 (дата обращения: 21.12.2025).



