При управлении ресурсами сложной системы необходимо учитывать множество факторов, оказывающих существенное влияние на процесс управления, качество принимаемых решений и результаты. В этой ситуации лицо, принимающее решения, нуждается в своевременном получении актуальной и релевантной информации, то есть требуется обеспечить поддержку принятия решений. Основная сложность этой поддержки заключается в том, что требуется учитывать динамично изменяющуюся внешнюю среду, многообразие имеющихся ресурсов, а также специфические особенности предметной области, которые зачастую являются слабоформализуемыми.
Анализ основных исследований [1–3, 7, 8] в области управления распределением ресурсов в сложных системах показал, что большинство разработанных методов работают в основном с числовыми данными и не учитывают слабоформализуемую информацию об особенностях предметной области, а также индивидуальные особенности, присущие ресурсам одного вида.
Данная статья посвящена разработке математического и программного обеспечения для информационной поддержки принятия решений при управлении ресурсами сложных систем с учетом динамично изменяющейся внешней среды и семантических ограничений предметной области. В первом разделе приведена постановка задачи управления ресурсами с учетом семантических ограничений предметной области и формализация задачи управления ресурсами. Во втором разделе представлено программное обеспечение прототипов СППР на базе многоагентного подхода.
Математическое обеспечение для информационной поддержки принятия решений при управлении ресурсами с использованием семантических ограничений предметной области
Задачи распределения ресурсов могут иметь разные формулировки, суть которых сводится к тому, что требуется оптимальным (или рациональным) образом распределить имеющиеся ресурсы для достижения определенных целей. Под оптимальностью в данном случае может пониматься некий критерий, позволяющий оценить качество распределения ресурсов, например таким критерием может быть максимум прибыли, минимум затрат и т.п. Имеются определенные ограничения на сами ресурсы и их использование при достижении целей.
Для обобщения таких задач вполне логично использовать единую терминологию. При формулировке классической задачи управления ресурсами будем использовать следующие понятия:
– «ресурсы» – это все то, что используется для решения каких-либо задач. В разных постановках в качестве ресурсов могут выступать станки, оборудование, специалисты;
– «потребители ресурсов» – это любые сущности, которые используют ресурсы для достижения своих целей и решения задач. В разных постановках в качестве потребителей ресурсов могут выступать детали.
Например, для изготовления детали требуются токарный, фрезерный и сверлильный станки, а также рабочие соответствующих специальностей. Тогда станки и рабочие будут ресурсами, а деталь – это потребитель ресурсов.
Рассмотрим формальную постановку классической задачи управления ресурсами.
Дано:
N – количество видов ресурсов;
M – количество потребителей ресурсов;
R = {r1, …, rn} – множество ресурсов, n = 1,..,N;
U = {u1, …, um} – множество потребителей ресурсов, m = 1,..,M;
Введем множество пар ρ = {ri/uj}, элементы которого ρij = ri/uj характеризуют распределение (выделение, назначение) ресурса ri для потребителя uj.
Введем критерий f(ρ), позволяющий оценить качество распределения. Требуется найти такое распределение ресурсов, чтобы значение этого критерия было бы максимальным f(ρ) → max.
Имеются три вида основных наиболее распространенных ограничений, которые могут быть представлены следующим образом:
O(R) – ограничения по ресурсам (по запасам, производственным мощностям, технологические ограничения и т.п.);
O(U) – ограничения по потребителям ресурсов (по производственной программе, например, нужно изготовить не менее k деталей);
O(R×U) – ограничения, связанные с конкретным распределением ресурсов (например, суммарное количество ресурсов, выделяемых на распределение, не должно превышать их общего количества).
Таким образом, классическая задача распределения ресурсами может быть сформулирована в следующем виде:
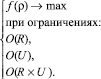 (*)
(*)
В то же самое время на практике очень часто возникают задачи, связанные с распределением ресурсов, которые не укладываются в классическую постановку. Это происходит из-за того, что при формулировке задачи распределения ресурсов приходится учитывать ряд ограничений, не представленных в (*).
В основном это сложно формализуемые семантические ограничения нечисловой природы. При попытке формализации таких ограничений и сведении такой задачи к классической постановке вида (*) получается достаточно громоздкая и трудно воспринимаемая модель. При этом чем более сложные ограничения рассматриваются, тем более трудоемок процесс сведения задачи к классической.
Для иллюстрации таких ограничений рассмотрим пример задачи доставки заказов покупателям, когда необходимо распределить имеющиеся в наличии транспортные средства (ресурсы) для доставки заказов (потребители ресурсов) покупателям. Помимо стандартных ограничений на вместимость грузов и т.п. вводится ограничение на несовместимость определенных видов заказов, например, продукты питания и бытовая химия не могут перевозиться одновременно на одном автомобиле. Это ограничение гораздо сложнее рассмотренных нами ранее и не укладывается в классическую постановку задачи распределения ресурсов (*). Формально записать такое ограничение можно в виде O(R×U×U). Это ограничение затрагивает только двух потребителей ресурсов. Классический пример такого рода ограничений представлен в задаче о перевозке волка, козы и капусты на лодке с одного берега на другой. Однако в общем случае ограничение может связывать несколько потребителей ресурсов и тогда в общем виде запишется как O(R×U×U×…×U).
Другой вид ограничений присутствует в задачах, когда потребителю ресурсов для достижения своей цели требуется не один, а несколько ресурсов. При этом ограничения обычно накладываются на порядок или технологию использования этих ресурсов. Для простого случая с двумя ресурсами ограничения представимы в виде O(R×R×U). В общем случае ограничение, накладываемое на использование нескольких видов ресурсов для конкретного потребителя ресурсов, запишется в виде O(R×R×…×R×U). В качестве примера задачи с такими ограничениями можно привести задачу с прохождением отдыхающими (потребители ресурсов) отдельных процедур (ресурсы) в медицинском учреждении [5]. При этом ограничения на несовместимость двух и более процедур или порядок прохождения этих процедур для конкретного отдыхающего (например, по медицинским показаниям) как раз укладываются в такую схему.
Более сложные ограничения, охватывающие несколько ресурсов и несколько потребителей ресурсов, описываются ограничениями вида O(R×R×…×R×U×U×…×U).
Таким образом, существуют постановки задач распределения ресурсов с использованием семантических ограничений, которые не всегда возможно свести к задаче (*) или же такое сведение нецелесообразно ввиду усложнения модели задачи. Поэтому в общем виде задача распределения ресурсов с использованием семантических ограничений запишется в виде
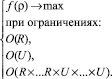
Для решения задачи управления ресурсами в сложных системах предлагается использовать многоагентные технологии. Любые сложноформализуемые семантические ограничения предметной области представляются в виде онтологической базы знаний, используемой агентами для решения задачи. Кроме этого, база знаний агента используется для описания критериев, отражающих приемлемость распределения ресурсов, и учитывает индивидуальные особенности моделируемых объектов реального мира. При ведении переговоров агенты определяют допустимость и приемлемость для них решения на основе индивидуальной базы знаний.
В качестве базовой используется модель агентов, предложенная Вулдриджем и Дженнингсом [10]. Агентам для решения задач распределения ресурсов соответствуют сущности, выступающие в реальном мире потребителями и/или поставщиками ресурсов, а также сами ресурсы. Для решения задачи распределения ресурсов агенты взаимодействуют и вступают в переговоры друг с другом, которые моделируются коммуникациями.
Ранее [3] был разработан обобщенный алгоритм решения задачи управления ресурсами с учетом семантических ограничений.
Многоагентные технологии позволяют успешно решать задачи управления ресурсами с учетом как глобальных, так и локальных критериев и позволяют учитывать уникальные свойства, присущие ресурсам одного вида, не усложняя при этом саму модель.
Рассмотрим далее формальное описание задачи управления ресурсами сложных систем.
Формально модель задачи управления ресурсами сложных систем с использованием многоагентных технологий может быть представлена в виде набора элементов < Agents, KB, Acts, E, Constraints, F > , где
Agents – множество агентов, участвующих в процессе решения задачи управления ресурсами;
KB – базы знаний агентов, которые содержат определенные знания и правила поведения;
Acts – множество возможных действий (поведений) агентов;
E – модель окружающей внешней среды, в которой функционирует сложная система;
Constraints – множество ограничений, в том числе и семантических, для данной предметной области;
F – множество критериев оценки производительности для каждого агента, а также общий критерий оценки всей системы в целом.
Предлагается рассматривать внешнюю среду как активный элемент системы, участвующий в решении задач управления ресурсами сложных систем. Факторы внешней среды, оказывающие влияние на управление ресурсами сложной системы, можно моделировать с помощью агентов. При этом взаимосвязи между факторами и их воздействие на элементы системы описываются при помощи онтологии. Такое представление позволяет более адекватно моделировать воздействие внешней среды и их последствия. Включение факторов внешней среды в качестве агентов позволяет получить единую многоагентную систему и использовать результаты такого моделирования для информационной поддержки принятия решений при управлении ресурсами.
Программное обеспечение для информационной поддержки принятия решений при управлении ресурсами сложных систем
Предлагаемая формализация задачи управления ресурсами сложных систем учитывает индивидуальные особенности моделируемых объектов реального мира, а также семантические ограничения предметных областей и позволяет получать допустимые планы распределения ресурсов в условиях множества критериев для обеспечения лица, принимающего решения, необходимой достоверной и обоснованной информацией. Она является основой разработки программного обеспечения прототипов информационной поддержки принятия решений при управлении ресурсами сложных систем в условиях динамично изменяющейся внешней среды.
Разработанные требования к программному обеспечению [3, 4] включают необходимость решения задачи информационной поддержки принятия решений при управлении ресурсами в режиме реального времени. Кроме этого, должна быть предусмотрена возможность отслеживания реализации разработанного и принятого плана распределения ресурсов и, в случае необходимости, оперативного внесения корректировок в случае непредвиденных обстоятельств или сбоев.
Предлагаемые идеи использования технологий искусственного интеллекта и инженерии знаний легли в основу разработки прототипов систем поддержки принятия решений для различных предметных областей: календарное планирование производства [6], распределение ресурсов в условиях чрезвычайных ситуаций [9], распределение ресурсов при оказании медицинских услуг [5].
В рамках дальнейших направлений исследований предполагается провести оценку эффективности предлагаемой концепции для решения задач управления ресурсами в сложных системах.
Заключение
Представлено математическое обеспечение для информационной поддержки принятия решений при управлении ресурсами, которое включает математическую модель задачи управления ресурсами с учетом семантических ограничений и формальное описание задачи управления ресурсами сложных систем. Программное обеспечение прототипов СППР разработано с использованием многоагентных технологий с учетом сформулированных требований.
Исследование частично поддержано грантами РФФИ 14-07-00811-а, 15-07-01565-а.
Рецензенты:
Картак В.М., д.ф.-м.н., профессор, зав. кафедрой прикладной информатики, Башкирский государственный педагогический университет им. М. Акмуллы, г. Уфа;
Сметанина О.Н., д.т.н., профессор, кафедра вычислительной математики и кибернетики, ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.
Библиографическая ссылка
Ризванов Д.А., Юсупова Н.И. МАТЕМАТИЧЕСКОЕ И ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ ИНФОРМАЦИОННОЙ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ ПРИ УПРАВЛЕНИИ РЕСУРСАМИ СЛОЖНЫХ СИСТЕМ // Фундаментальные исследования. 2015. № 10-2. С. 294-298;URL: https://fundamental-research.ru/ru/article/view?id=39167 (дата обращения: 07.03.2026).



