В 3-мерном пространстве S подмножество A ⊂ S образуют экспериментально измеренные значения sj ∈ S, j = 1...M параметров s = {s1, s2, s3}. Экспертное правило прогноза одних параметров η из числа si, i = 1...N, по измеренным другим, обозначаемым ξ: s = ξ×η определяется данными A ⊂ S, являющимися экспериментальным основанием. В задачах промысловой геофизики петрофизические зависимости традиционно являются таким экспертным правилом [1], представляя данные A в виде регрессионных зависимостей одних параметров от других. Данный способ обширно используется в настоящее время, но он не принимает во внимание объективные свойства неоднородностей в изучаемых параметрах.
Правило 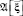 вывода результата о прогнозируемых параметрах
вывода результата о прогнозируемых параметрах 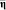 посредством использования информации об измеренных параметрах
посредством использования информации об измеренных параметрах 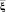 , связанное с обучающими данными A ⊂ S, реализуется посредством: определения нечеткого отношения μA(ξ, η) = μA(s) по обучающей выборке A [5] между параметрами η и ξ; представления конкретных измерений
, связанное с обучающими данными A ⊂ S, реализуется посредством: определения нечеткого отношения μA(ξ, η) = μA(s) по обучающей выборке A [5] между параметрами η и ξ; представления конкретных измерений 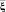 в виде нечеткой величины и последующего использования алгоритма нечеткого логического вывода [3] о нечеткой величине η.
в виде нечеткой величины и последующего использования алгоритма нечеткого логического вывода [3] о нечеткой величине η.
Поле рассеяния является основанием для отображения данных A в виде нечетких отношений, а измеренных значений параметра 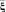 , с помощью которых выполняется прогноз, в виде нечетких величин.
, с помощью которых выполняется прогноз, в виде нечетких величин.
Полем рассеяния для данных sj ∈ S, j = 1...M является такая функция Aε(s) в пространстве, что для каждой подобласти ΔS пространства S:
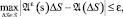 (1)
(1)
где A(ΔS) – число значений из A ⊂ S, целиком лежащее в ΔS.
Функцией принадлежности μA(s) для измеренных значений параметров s ∈ S в виде нечетких величин является нормированное к единице поле рассеяния Aε(s).
Для того чтобы построить поле рассеяния Aε(s), необходимо пространство S разбить сеткой ΔSk, k = 1...K, покрывающей всю область значений параметров из A, 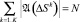 , и поставить задачу нахождения функции рассеяния по (1):
, и поставить задачу нахождения функции рассеяния по (1):
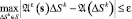 . (2)
. (2)
Необходимо выбрать базисную систему функций K(h, s), параметризованную вектором параметров h, и поставить задачу нахождения Aε(s) в виде
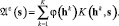 (3)
(3)
Функция φ(hk) требует нахождения из (2). Выражение (3) показывает, что поле рассеяния рассчитывается в виде линейной комбинации базовых функций K(h, s), определяющих метод для аппроксимации поля рассеяния Aε(s), а также функции принадлежности μA(s).
Для аппроксимации функции принадлежности принято использовать треугольные трапециевидные и другие ранее вводимые зависимости [2]. В противоположность данным принципам для элемента аппроксимации K(h, s) введем метод максимальной энтропии. Согласно данному методу в качестве элемента аппроксимации была использована функция нормального закона распределения [4], параметром h в котором является математическое ожидание:
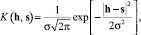 (4)
(4)
где σ2 – дисперсия нормального распределения.
Из выражения (3) получаем
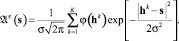 (5)
(5)
Выражение (5) поясняется как диффузионное рассеяние в бесконечном однородном пространстве параметров точечных источников, расположенных в hk. По описанному принципу расчета аппроксимации функции принадлежности произведем вычислительный эксперимент.
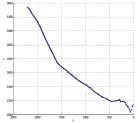
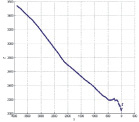
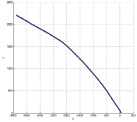
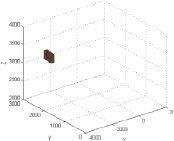
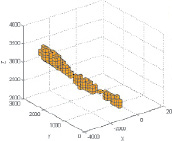
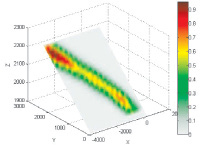
В результате измерений получено следующее отношение между характеристиками, где X – абсолютная глубина; Y – двойное время ВСП (вертикальное сейсмическое профилирование), а Z – средняя скорость.
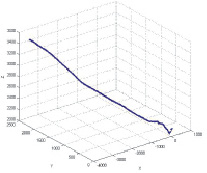
Рис. 1. Зависимость между абсолютной глубиной, двойным временем ВСП и средней скоростью
Для более наглядного отображения представлены проекции на плоскости YZ, XZ и XY (табл. 1).
Таблица 1
Проекция на плоскости
|
Проекция на плоскость YZ |
Проекция на плоскость XZ |
Проекция на плоскость XY |
|
|
|
|
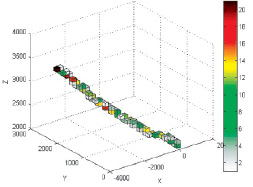
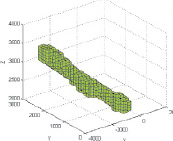
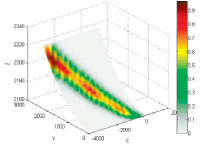
Рис. 2. Карта плотности данных (справа легенда по параметру количества данных, попавших в ячейку)
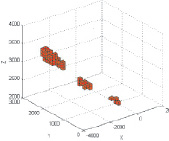
На основе данного отношения была получена карта плотности данных (см. рис. 2). Картой плотности называется отношение числа данных для каждого выделенного интервала к общему числу данных.
На основе приведенной карты плотности данных необходимо построить карту источников информации. Очевидно, что чем больше источников на карте, тем меньше погрешность при аппроксимации функции принадлежности, отсюда следует задача поиска оптимального количества источников.
Метод состоит в следующем: задается уровень погрешности и по невязке определяется необходимое количество источников. Далее проведем расчеты для поставленной задачи.
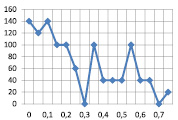
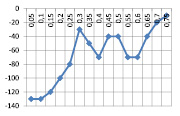
На рис. 3 представлен график исходных данных. Погрешность считалась по формуле (1).
На основе данного графика мы можем просмотреть отношение приращения количества источников к приращению погрешности по формуле (6), что покажет скорость изменения количества источников относительно предыдущего шага (табл. 2).
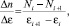 (6)
(6)
где Ni – это значение количества источников при текущем значении погрешности εi.
Из чего мы можем сделать вывод: для данного эксперимента оптимальной погрешностью являются значения 0,3 и 0,7, при этом значения количества источников соответственно равны 26 и 6, так как отношение приращения количества источников к приращению погрешности на данном отрезке дает наименьший результат.
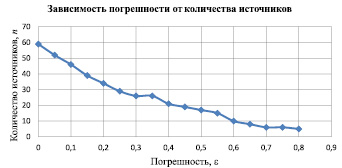
Рис. 3. Зависимость погрешности от количества источников
Таблица 2
Поиск оптимального количества источников
|
1 |
Скорость изменения |
2 |
Скорость нарастания количества источников с изменением погрешности |
|
Δn/Δε |
|
∂n/∂ε |
|
|
Погрешность, ε |
Погрешность, ε |
||
|
3 |
Изменение количества источников относительно всего объема данных |
||
|
ΔN/ΔE |
|
||
|
Погрешность, ε |
|||
Далее была рассчитана зависимость скорости нарастания количества источников от увеличения погрешности, которая рассчитывается как производная в каждой точке (табл. 2). Так как производная в точке равна углу наклона касательной, проведенной через данную точку, в качестве касательной была рассчитана прямая проходящая через прилежащие точки (7):
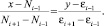 (7)
(7)
Как видно на графике, скорость нарастания количества источников ближе к нулю при значениях погрешности 0,3 и 0,7, при этом количество источников равно 26 и 6.
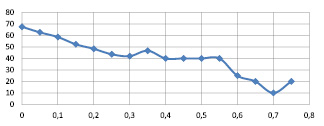
Также рассчитываем изменение количества источников относительно всего объема данных по формуле (8), что позволит найти оптимальное значение погрешности, учитывая весь объем выборки (табл. 2).
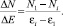 (8)
(8)
Минимумы изменения количества источников относительно всего объема данных (59 возможных источников) при значениях 0,3; 0,4 и 0,7, при этом количество источников равны 26, 21 и 6.
Вывод: оптимальное количество источников для данного эксперимента ‒ не менее 26. Погрешность при данном количестве источников равна 0,3.
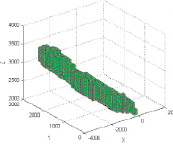
После нахождения оптимального количества источников была построена карта источников информации (рис. 4), построенное поле рассеяния по которой, наиболее соответствует наблюдаемым данным.
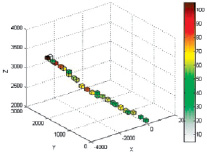
Рис. 4. Карта источников (справа легенда по параметру значений в источниках)
Таблица 3
Поле рассеяния, дифференцированное по уровню доверия
|
α = 0,9; уровень доверия = 0,1 |
α = 0,8; уровень доверия = 0,2 |
|
|
|
|
α = 0,7; уровень доверия = 0,3 |
α = 0,6; уровень доверия = 0,4 |
|
|
|
|
α = 0,5; уровень доверия = 0,5 |
α = 0,4; уровень доверия = 0,6 |
|
|
|
|
α = 0,3; уровень доверия = 0,7 |
α = 0,2; уровень доверия = 0,8 |
|
|
|
Таблица 4
Сечение поля рассеяния плоскостями
|
Прямой плоскостью, проходящей через два максимальных источника (справа легенда по параметру функции принадлежности) |
Изогнутой плоскостью, проходящей через все максимальные источники (справа легенда по параметру функции принадлежности) |
|
|
|
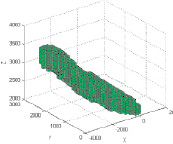
На основании карты были рассчитаны поля рассеяния. Ниже приведен пример построенного поля рассеяния, дифференцированный по уровню доверия (табл. 3).
Чтобы лучше понять данное поле рассеяние, представлены сечения (табл. 4).
Рецензенты:
Бурмистрова О.Н., д.т.н., профессор, заведующая кафедрой ТМЛ, Ухтинский государственный технический университет, г. Ухта;
Некучаев В.О., д.ф.-м.н., профессор, заведующий кафедрой физики, Ухтинский государственный технический университет, г. Ухта.
Библиографическая ссылка
Кобрунов А.И., Дорогобед А.Н., Кожевникова П.В. АППРОКСИМАЦИЯ ТРЕХМЕРНЫХ СВЯЗЕЙ НА ОСНОВЕ ТЕХНОЛОГИЙ МНОГОВАРИАНТНОГО МОДЕЛИРОВАНИЯ // Фундаментальные исследования. 2015. № 10-2. С. 268-273;URL: https://fundamental-research.ru/ru/article/view?id=39162 (дата обращения: 07.03.2026).