При моделировании технологических процессов изначально требуется получить данные о свойствах материалов экспериментальным путем, а затем, основываясь на полученных результатах, проводить численные исследования. Теплофизические свойства полимеров описаны во многих трудах различных авторов [3, 4, 6, 8]. Следует отметить, что на сегодняшний день в открытой литературе опубликован целый ряд работ по исследованию теплофизических свойств полимеров [1, 9, 10]. Однако недостаточно полно представлены практические рекомендации, позволяющие перейти от натурного эксперимента к моделированию реальных технологических процессов.
Таким образом, представляет научный интерес и является весьма актуальной разработка универсального подхода по совмещению эксперимента и численного исследования.
Научной новизной работы является описание практических рекомендаций, которые позволят, используя современное оборудование и математическое моделирование, спрогнозировать скрытые особенности поведения материала в реальных технологических процессах.
Использование предложенных практических рекомендаций позволит сократить временные и материальные затраты на производстве при изучении технологических процессов, связанных с переработкой полимеров.
В качестве примера рассматривался процесс плавления полимеров, происходящий в дифференциально-сканирующем калориметре [5].
Было проведено 5 экспериментальных исследований теплофизических свойств для трёх марок полиэтилена: ПЭ 271-274K, Megolon HF 1876, ПЭ 153-02K. На рис. 1 сопоставлены температурные зависимости удельной теплоёмкости при скорости нагрева 10 °C/мин.
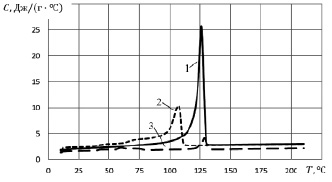
Рис. 1. Температурные зависимости удельной теплоёмкости материалов: 1 – ПЭ 271-274К; 2 – ПЭ 153-02К; 3 – безгалогенный компаунд Megolon HF 1876
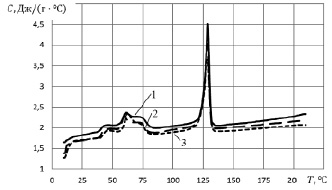
Рис. 2. Температурные зависимости удельной теплоёмкости для безгалогенного компаунда Megolon HF 1876 при разных скоростях нагрева: 1 – 5 °С/мин; 2 – 10°С/мин; 3 – 20 °С/мин
Проанализировав данные графики, можем сделать вывод, что материал ПЭ 271-274K является более термоустойчивым, в отличие от остальных. Его скрытая теплота плавления превышает теплоты двух других материалов и равна 270,1 Дж/г, а у материалов Megolon HF 1876 и ПЭ 153-02K она равна 200,9 и 75,85 Дж/г соответственно. Это говорит о том, что для его плавления требуется большее количество тепла. Также об этом свидетельствуют значения удельной теплоёмкости в температурном диапазоне плавления. Максимальное значение удельной теплоёмкости для этого материала достигает значения 25,8 Дж/(г∙°С), в то время как у материалов Megolon HF 1876 и ПЭ 153-02K она равна соответственно 4,047 и 10,38 Дж/(г∙°С).
На рис. 2 сопоставлены графики зависимостей теплоёмкости от температуры для материала Megolon HF 1876 при разных скоростях нагрева. Проанализировав данные графики, можно увидеть, как скорость нагрева влияет на процесс плавления. Чем выше скорость нагрева, тем меньше скрытая теплота плавления материала, следовательно, тем меньше требуется тепла для перехода материала из твёрдого состояния в жидкое. Для скорости 5 °С/мин скрытая теплота плавления равна 76,2 Дж/г, при скорости 10 °С/мин она равна 75,85 Дж/г , а для скорости 20 °С/мин она равна 75,26 Дж/г.
Также по температурному диапазону плавления видно, что при большей скорости нагрева материал начинает плавиться раньше, чем при меньшей скорости. Скорости нагрева 5 °С/мин соответствует температурный диапазон плавления (125,34–128,84) °С, скорости 10 °С/мин – (124,4–128,45) °С, скорости 20 °С/мин – (123,49–128,52) °С.
После экспериментального исследования теплофизических свойств рассматриваемых материалов было проведено численное исследование.
Математическое описание процесса плавления в дифференциально-сканирующем калориметре основывается на законе сохранения энергии. Решение общей задачи осуществляется поэтапно [7].
Поскольку реальные процессы теплообмена сложны, для возможности их моделирования и упрощения системы примем следующие допущения:
● задача осесимметричная;
● свойства материала однородны, изотропны;
● теплофизические свойства материала постоянны, за исключением теплоёмкости (зависит от температуры);
● отсутствуют внутренние источники тепла (отсутствует тепло за счет отсутствия диссипации);
● тепловым потоком 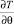 пренебрегаем;
пренебрегаем;
● материал находится в неподвижном состоянии.
Уравнение энергии, исходя из принятых допущений, примет следующий вид:
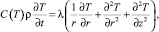 (2)
(2)
где C(T) – удельная теплоёмкость материала, Дж/(кг∙°С) (является функцией от температуры); ρ – плотность материала, кг/м3; λ – теплопроводность материала, Вт/(м∙°С).
Уравнение (2) необходимо дополнить условиями однозначности.
Температура во всем объеме материала в начальный момент времени t = 0 равна T0, °С.
T(r, z, 0) = T0. (3)
В данной задаче используются граничные условия 1-го рода, задаётся значение функции Т(r, z, t) на границах для каждого момента времени:
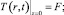 (4)
(4)
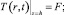 (5)
(5)
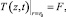 (6)
(6)
где F = f(t) – функция по времени; h – высота исследуемой модели, м; r0 – радиус модели, м.
f(τ) = T0 + ΔT∙t, (7)
где ΔT – скорость нагрева, °С/с.
Таким образом, уравнение (2), замкнутое условиями однозначности (3)–(7), является математической моделью процесса плавления.
В результате моделирования процесса плавления, проходящего в дифференциально-сканирующем калориметре, были получены следующие результаты, которые представлены ниже. При численной реализации в пакете ANSYS температурная зависимость теплоёмкости, скрытая теплота плавления и температурный диапазон плавления материала взяты из экспериментальных данных. Для удельной теплоёмкости из всего распределения выбраны опорные точки, отображающие изменение состояния материала. Плотность и теплопроводность взяты из справочника [2].
На рис. 3 просматривается появление областей расплава в объёме материала. Это говорит о начале плавления. Для оценки невязки сравнивались температурные диапазоны плавления материалов. Результаты сравнительного анализа представлены в таблице.
Оценка невязки
|
Номер опыта |
Материал |
Скорость нагрева, °С/мин |
Температура начала плавления, °С |
Невязка, % |
Температура конца плавления, °С |
Невязка, % |
||
|
Эксп. |
Расч. |
Эксп. |
Расч. |
|||||
|
1 |
ПЭ 271-274К |
10 |
121,44 |
121,67 |
0,18 |
126,06 |
126,67 |
0,48 |
|
2 |
ПЭ 153-02К |
10 |
98,82 |
98,34 |
0,49 |
107,15 |
107,5 |
0,33 |
|
3 |
Megolon HF 1876 |
5 |
125,34 |
125,78 |
0,35 |
128,84 |
128,7 |
0,11 |
|
4 |
10 |
124,4 |
124,17 |
0,18 |
128,45 |
128,34 |
0,09 |
|
|
5 |
20 |
123,49 |
123,99 |
0,40 |
128,52 |
128,67 |
0,12 |
|
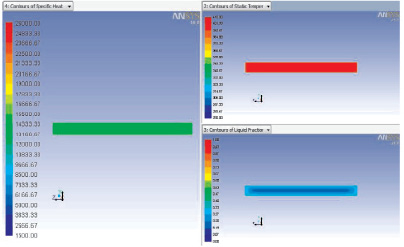
Рис. 3. Сечение YZ, t = 670 с. Слева: теплоемкость материала; справа вверху: температура; справа внизу: содержание жидких фракций
По результатам таблицы можно отметить, что отклонение расчетных значений от экспериментальных не превышает 5 %. Это говорит о том, что представленная математическая модель является адекватной.
Таким образом, совместное использование натурного эксперимента и численного исследования дает возможность для дальнейшего моделирования более сложных технологических процессов.
Рецензенты:
Щербинин А.Г., д.т.н., доцент, профессор кафедры «Конструирование и технологии в электротехнике», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Труфанова Н.М., д.т.н., профессор, зав. кафедрой «Конструирование и технологии в электротехнике», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Библиографическая ссылка
Казаков А.В., Петренко А.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ПЛАВЛЕНИЯ ПОЛИМЕРА // Фундаментальные исследования. 2015. № 10-2. С. 264-267;URL: https://fundamental-research.ru/ru/article/view?id=39161 (дата обращения: 23.01.2026).



