Целью настоящего исследования является разработка модельно-компьютерного инструментария и методики оценки влияния длины исходной совокупности выборочных данных на прогнозные величины социально-экономических показателей.
Для достижения этой цели решены следующие задачи: изучены основные понятия, связанные с сущностью, методами и методиками анализа и прогнозирования социально-экономических показателей регионов; создано информационное обеспечение, необходимое для анализа и прогнозирования шести ключевых показателей регионов РФ по данным за 2002–2013 гг.; разработан модельно-компьютерный инструментарий для автоматизации расчетов и процедур обработки информации, связанных с прогнозированием, представляющий собой совокупность взаимосвязанных таблиц-шаблонов для исходных, промежуточных и итоговых данных, а также для выполнения процедур обработки информации с встроенными в них формулами; сформулирован ряд выводов на основе различных вариантов прогнозов ключевых социально-экономических показателей по Республике Дагестан, рассчитанных с помощью модельно-компьютерного инструментария.
Для достижения цели и решения поставленных задач по литературным источникам (учебного, справочного и научного характера) нами изучены различные трактовки понятий: анализ, прогноз и прогнозирование; экономические показатели и их временные ряды; методы и виды анализа и прогнозирования; длина исходного временного интервала и прогнозный горизонт; экстраполяция и интерполяция и др. [4–8]. Результаты деятельности экономических объектов находят количественное выражение в экономических показателях, отражающих объем, размер, структуру, уровень, экономическую эффективность процессов. Такие показатели могут быть получены из отчетных данных или в результате их обработки и преобразования.
«Показатель» представляет собой признак, поддающийся количественной оценке и используемый для вынесения суждения о некотором процессе, объекте или явлении. В экономике различают абсолютные, относительные, суммарные, средние и др. показатели. С понятием «показатель» тесно связаны понятия «фактор» и «алгоритм». Фактором называют причину, движущую силу какого-то процесса или явления, определяющую его характер или отдельные черты, а алгоритм представляет собой способ решения некоторой задачи, точно предписывающий действия, которые нужно совершить для получения результата, зависящего от исходных данных.
Анализ и прогнозирование являются наиболее сложными из функций управления, выполняемых экономическими объектами. Экономический анализ представляет собой систематизированную совокупность аналитических процедур, имеющих целью получение заключений, выводов и рекомендаций экономического характера в отношении некоторого объекта [7]. Одной из основных целей анализа в экономике является выявление тенденций в изменении показателей, а также связей и зависимостей между ними.
Связью в экономике называют совместное изменение двух или более показателей. Среди связей важную роль играет причинная связь, сущность которой состоит в порождении одного явления другим. Такие связи называются зависимостями. При этом показатели, характеризующие причины, называются факторными, или независимыми переменными, а показатели, характеризующие следствие, – результативными, или зависимыми переменными. С помощью связей и зависимостей между показателями экономических объектов, представленных в виде статистической совокупности данных в пространстве и времени, могут быть выявлены те или иные тенденции. Тенденция – это стремление, свойственное чему-нибудь; направление развития какого-либо явления. Определить динамические тенденции означает выявить наличие: определенных закономерностей в изменении отдельного экономического показателя во времени; закономерностей в изменении структурного состава того или иного экономического показателя во времени; связи, зависимости или закономерности в изменении значений одного (зависимого) из экономических показателей во времени при изменении значения одного, двух и более других (независимых) показателей [3].
Особую роль среди связей и зависимостей играют те, которые могут быть выражены в виде формул. Выявление и построение таких формул принято называть процессом моделирования.
Выявленные в результате анализа тенденции и динамические связи являются основой прогнозирования. Из множества существующих определений понятия «прогноз» в экономике [см., например, 3–11] одним из удачных, по мнению авторов, является следующее: «Прогноз – это расчет неизвестного экономического показателя по заданным факторам на основании модели». При этом система научных исследований качественного и количественного характера, направленных на выяснение тенденций развития народного хозяйства или его частей (отраслей, регионов, предприятий и т.п.), называется прогнозированием. Важной характеристикой прогнозирования является длина прогнозного горизонта, которая по учебным литературным источникам должна составить примерно одну треть длины исходного интервала [5; 11].
Для анализа и прогнозирования в экономике разработано множество методов. Любой метод прогнозирования базируется на идее экстраполяции, под которой обычно понимают распространение закономерностей, связей и соотношений, действующих в исходном временном периоде, за его пределы [10].
Динамические тенденции зависят в первую очередь от длины исследуемого временного интервала. Поэтому чтобы выбрать приемлемые для реализации варианты прогнозов, возникает необходимость выявления тенденций за различные временные интервалы, проведения их сравнительного анализа, а также выполнения прогнозных расчетов и их сравнительной оценки при различных тенденциях.
Анализ динамических тенденций и прогнозирование предполагают наличие соответствующей исходной информационной базы данных. Информационной основой настоящего исследования является таблица с шестью социально-экономическими показателями в разрезе регионов России за 12 лет (2002–2013 гг.), сформированная в MS Excel из созданной и поддерживаемой нами с 2004 г. по настоящее время базы данных. Сама база данных представляет собой совокупность таблиц, публикуемых Росстатом в ежегоднике «Россия в цифрах» [9], а также совокупность рассчитанных авторами настоящего исследования таблиц, содержащих величины темповых, структурных, суммарных, средних, относительных и др. показателей.
Анализ и прогнозирование, как известно, связаны с множеством расчетов, выполнение которых обеспечивается различными математическими формулами. Их взаимосвязанную совокупность принято называть алгоритмом или математической моделью. В соответствии с созданной авторами исходной таблицей анализ и прогнозирование для каждого из 88-ми экономических объектов (79 регионов, 8 федеральных округов, страна в целом) можно проводить по одной и той же модели, созданной для одного объекта (региона, федерального округа или страны в целом). Математическая модель сама по себе не выполняет никаких расчетов; формулы, включенные в ее состав, лишь показывают, как следует рассчитать тот или иной показатель. Сами же расчеты при этом можно выполнять вручную или на ЭВМ. Для выполнения расчетов по математической модели на ПЭВМ требуется преобразовать ее в компьютерную модель.
На примере Республики Дагестан нами созданы математическая и компьютерная модели, обеспечивающие автоматизацию расчетов, связанных с разработкой вариантов прогнозов для одного региона, по которым могут быть выполнены расчеты для любого из остальных регионов (федерального округа, страны в целом).
Математическая модель представляет собой совокупность формул, необходимых для построения уравнений временных рядов и рядов динамики пяти видов (линейных, показательных, гиперболических, степенных и параболических), т.е. для расчета параметров уравнений (свободного члена и коэффициентов при переменных) и статистических характеристик (дисперсий для зависимой и независимых пременных, индексов корреляции и детерминации, критериев Фишера и Стьюдента, средней ошибки аппроксимации и др.). Компьютерная модель обеспечивает выполнение всех предусмотренных математической моделью расчетов на ПЭВМ и включает в себя совокупность всей цепочки взаимосвязанных таблиц-шаблонов, в ячейки которых встроены все расчетные формулы и операторы, обеспечивающие различные процедуры обработки информации [3].
Важными составляющими компьютерной модели являются графики-шаблоны, позволяющие строить графики изменения каждого показателя и графики точек рассеивания для выявления наличия или отсутствия зависимости (связи) между парами экономических показателей. Анализ графиков, построенных авторами по данным трех ключевых относительных показателей по данным РД, показал, что для описания тенденций и динамических связей (зависимостей) вполне приемлемы три вида уравнений временных рядов и рядов динамики: линейного, показательного и степенного видов. Поэтому в настоящей статье нет необходимости обосновать выбор вида уравнений временных рядов и рядов динамики для прогнозирования расчетами и оценкой статистических характеристик.
В настоящей статье не рассчитываются и не анализируются параметры уравнений и их статистические характеристики. То есть, задачей модельно-программного инструментария является выполнение прогнозных расчетов по уравнениям без построения самых уравнений. Это обеспечивается включением в компьютерную модель встроенных статистических функций «тенденция» и «рост» из MS Excel, первая из которых обеспечивает выполнение прогнозных расчетов по уравнениям линейного вида, вторая – по уравнениям показательного вида.
В принципе функция «тенденции» может обеспечить выполнение расчетов по любому из пяти рассматриваемых параметров, поскольку все они могут быть преобразованы в линейный вид. Но поскольку для уравнения показательного вида имеется специальная функция «рост», то целесообразно и ее использование.
Иными словами, разработанный нами инструментарий выполняет прогнозные расчеты для 4-х видов уравнений с помощью функции «тенденция», а для показательного вида уравнений – с помощью функции «рост».
Чтобы преобразовать уравнение степенного вида (например, 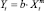 ) в линейный вид, принято логарифмировать обе части степенного уравнения. В результате в нашем случае получим
) в линейный вид, принято логарифмировать обе части степенного уравнения. В результате в нашем случае получим
lgYt = lgb + m∙lgXt,
т.е. для степенной функции сначала рассчитываются прогнозные значения для lgYt по величинам lgXt (с помощью функции «тенденция»), а затем, потенцируя прогнозные значения lgYt и lgXt, рассчитываются прогнозные величины Yt и Xt.
Таким образом, для выполнения прогнозных расчетов в модельно-компьютерный инструментарий включены две математические («log10», «степень») и две статистические («тенденция», «рост») функции из MS Excel.
Отметим, что для прогнозирования разработаны и используются различные программные продукты и системы. Однако процесс прогнозирования настолько сложен, многогранен и разнороден, что в рамках одного программного продукта или системы нельзя предусмотреть все возникающие на практике прогнозирования ситуации, учесть все особенности различных экономических систем и все множество разнородных задач.
Задача настоящего исследования ограничена рамками разработки инструментария (математического и компьютерного) для сравнительной оценки вариантов прогнозов при выборе различных длин временного интервала исходной совокупности данных.
Разработанный нами модельно-компьютерный инструментарий предусматривает прогнозирование по уравнениям временных рядов (Yt = f(t)), а также по одно- и двухфакторным уравнениям рядов динамики (Yt = f(Xt); Yt = f(X1t, X2t)).
Отметим, что прогнозные расчеты выполняются по трем относительным показателям (производительности труда – Пт, фондовооруженности труда – Фв и средней месячной заработной платы – Зп); три абсолютных показателя включены в исходную таблицу, для того чтобы на их основе рассчитать два из относительных показателей (производительность и фондовооруженность труда). Ценность трех абсолютных показателей, включенных в исходную таблицу, не ограничивается расчетом на их основе производительности и фондовооруженности труда. По их величинам можно: во-первых, выполнить такие же прогнозные расчеты, как для относительных показателей; во-вторых, строить модели производственных функций, широко известные как функции Кобба ~ Дугласа [3; 11]. Однако в настоящей статье эти показатели не исследуются.
Перейдем теперь к описанию методики прогнозирования. Все прогнозные расчеты для одного региона выполняются десять раз при разных длинах исходного временного интервала.
При этом расчеты при каждой длине исходного интервала выполняются следующим образом:
– создается таблица-шаблон, предусматривающая выполнение всех расчетов по данным за один временной интервал (например, в нашем случае по данным за 12 лет);
– создаются десять ее копий;
– во всех таблицах-шаблонах копий, начиная со 2-й, удаляются 1-я, 2-я, 3-я и т.д. строки (соответственно за 2002 г.; за 2002–2003 гг.; за 2002–2004 гг. и т.д.).
В таблице приведены варианты прогнозов трех рассматриваемых показателей, рассчитанных по уравнениям временных рядов линейного и степенного видов по данным за восемь различных временных интервалов: 2002–2013; 2003–2013; …; 2009–2013 гг. Во всех случаях горизонт прогнозирования выбран один и тот же (2014, 2015, 2016 гг.).
По данным таблицы можно сформулировать ряд выводов, в частности:
– в соответствии с прогнозными величинами производительности труда, полученными по уравнениям при тенденции, имевшей место за весь 12-летний интервал времени (1 вариант) прогнозная величина в 2014 г. должна была составить 395,1 тыс. руб.; при тенденциях 2–6-го вариантов – 406,4–426,6 тыс. руб.; при тенденциях, сложившихся в 7–8-й варианты, прогнозная величина производительности труда меньше, чем в 5–6-м, но больше, чем в 1–4-м вариантах; при степенной зависимости по сравнению с линейной прогнозные величины производительности труда существенно меньше во всех вариантах;
– анализ прогнозных величин заработной платы при линейном уравнении показывает: во-первых, их рост по вариантам от 1-го по 8-й с 16003 до 18305 руб.; во-вторых, то что заработная плата в 2016 г. составила 18581–22294 руб., а ее приросты по сравнению с 2014 г. составили за два года 15-21 %; при степенной зависимости прогнозные величины заработной платы в 2014 г. оказались в пределах 13334–16420 руб, что существенно меньше, чем при линейной;
– прогнозные величины фондовооруженности труда в 2014 г. от 1-го по 6-й варианты составили 902,0–1002,1 тыс. руб., а по 7–8-му вариантам оказались примерно равными и были чуть меньше, чем по 6-му варианту. Отношение ее прогнозных значений по 6-му варианту к 1-му составило 111 %, что существенно меньше, чем аналогичные соотношения по производительности труда и заработной плате.
Варианты прогнозов производительности труда, средней месячной заработной платы и фондовооруженности труда, рассчитанные по исходным данным РД за различные временные интервалы с помощью уравнений временных рядов
|
Линейного вида |
Степенного вида |
|||||
|
2014 |
2015 |
2016 |
2014 |
2015 |
2016 |
|
|
Производительность труда, тыс. руб. |
||||||
|
2002–2013 |
395,1 |
427,5 |
459,9 |
339,7 |
364,0 |
388,2 |
|
2003–2013 |
406,4 |
441,3 |
476,3 |
374,0 |
403,4 |
432,6 |
|
2004–2013 |
411,8 |
448,2 |
484,5 |
368,8 |
394,9 |
420,6 |
|
2005–2013 |
418,3 |
456,4 |
494,5 |
377,1 |
403,0 |
428,1 |
|
2006–2013 |
424,2 |
464,1 |
503,9 |
389,7 |
416,3 |
441,9 |
|
2007–2013 |
426,6 |
467,3 |
507,9 |
397,3 |
423,3 |
447,9 |
|
2008–2013 |
422,4 |
461,4 |
500,5 |
391,3 |
413,0 |
433,2 |
|
2009–2013 |
419,5 |
457,3 |
495,2 |
391,7 |
411,2 |
428,9 |
|
Средняя месячная заработная плата, руб. |
||||||
|
2002–2013 |
16003 |
17292 |
18581 |
13334 |
14190 |
15037 |
|
2003–2013 |
16448 |
17840 |
19231 |
14204 |
15166 |
16115 |
|
2004–2013 |
16803 |
18284 |
19764 |
14624 |
15601 |
16556 |
|
2005–2013 |
17148 |
18723 |
20298 |
15093 |
16093 |
17064 |
|
2006–2013 |
17439 |
19100 |
20762 |
15405 |
16393 |
17342 |
|
2007–2013 |
17756 |
19523 |
21291 |
15909 |
16932 |
17903 |
|
2008–2013 |
17906 |
19730 |
21554 |
15939 |
16871 |
17738 |
|
2009–2013 |
18305 |
20299 |
22294 |
16420 |
17400 |
18296 |
|
Фондовооруженность труда, тыс. руб. |
||||||
|
2002–2013 |
902,0 |
962,9 |
1023,8 |
734,2 |
762,7 |
790,3 |
|
2003–2013 |
930,5 |
998,0 |
1065,5 |
787,8 |
823,2 |
857,5 |
|
2004–2013 |
947,9 |
1019,8 |
1091,6 |
809,8 |
846,7 |
882,2 |
|
2005–2013 |
971,8 |
1050,1 |
1128,4 |
855,1 |
898,1 |
939,2 |
|
2006–2013 |
987,5 |
1070,5 |
1153,5 |
883,8 |
929,4 |
972,6 |
|
2007–2013 |
1002,1 |
1090,0 |
1177,9 |
918,7 |
968,3 |
1015,0 |
|
2008–2013 |
1001,3 |
1088,9 |
1176,5 |
924,2 |
970,4 |
1013,0 |
|
2009–2013 |
1001,7 |
1089,5 |
1177,2 |
937,0 |
981,9 |
1022,4 |
В отличие от фондовооруженности труда, которую можно прогнозировать только с помощью уравнений временных рядов, производительность труда и заработную плату можно прогнозировать и по уравнениям рядов динамики. При этом отметим, что прогнозирование с помощью уравнений рядов динамики для таких показателей как производительность труда и заработная плата, которые зависят от различных показателей-факторов, в т.ч. и друг от друга, предпочтительнее, чем по уравнениям временных рядов.
Нами выполнены расчеты и построены прогнозные таблицы по уравнениям рядов динамики:
а) для зависимости производительности труда от фондовооруженности, от заработной платы и от обоих этих показателей;
б) для зависимости средней месячной заработной платы от фондовооруженности, от производительности труда и от обоих этих показателей.
Выводы, которые могут быть сформулированы по результатам, рассчитанным по уравнениям рядов динамики для зависимости производительности труда от фондовооруженности, от заработной платы и от обоих этих показателей:
– при линейных видах уравнений, выражающих зависимости производительности труда, разница между ее максимальным и минимальным прогнозными значениями на 2014 г. составила 36,3 тыс. руб. (или 8–9 %), а на 2016 г. – 54,1 (или 11–12 %);
– прогнозные значения производительности труда по одним и тем же вариантам, рассчитанным по уравнениям разных зависимостей, различаются между собой в еще меньшей степени (2–5 %).
Выводы о величинах прогнозных значений средней месячной заработной платы, рассчитанных по уравнениям ее зависимости от фондовооруженности, от производительности труда и от обоих этих показателей, которые можно сформулировать по полученным нами результатам расчетов:
– разница между max и min средней заработной платы за 2014 г. при разных временных интервалах составляет по линейным уравнениям рядов динамики 2392 руб. (max = 18225; min = 15833) или 13 и 15 %;
– разница в прогнозных значениях, рассчитанных по трем уравнениям для разных зависимостей для одних и тех же вариантов, является весьма незначительной и составляет 1–2 %.
Рецензенты:
Алиев М.А., д.э.н., профессор кафедры экономической теории, ФГБОУ ВПО «Дагестанский государственный педагогический университет», г. Махачкала;
Шахбанов Р.Б., д.э.н., профессор, зав. кафедрой бухгалтерского учета, ФГБОУ ВПО «Дагестанский государственный педагогический университет», г. Махачкала.
Библиографическая ссылка
Адамадзиев К.Р., Адамадзиева А.К. МОДЕЛЬНО-КОМПЬЮТЕРНЫЙ ИНСТРУМЕНТАРИЙ И МЕТОДИКА ЕГО ПРИМЕНЕНИЯ ДЛЯ ОЦЕНКИ ВЛИЯНИЯ ВРЕМЕННОГО ИНТЕРВАЛА ИСХОДНЫХ ДАННЫХ НА ПРОГНОЗ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ РЕГИОНОВ // Фундаментальные исследования. 2015. № 10-1. С. 121-126;URL: https://fundamental-research.ru/ru/article/view?id=39134 (дата обращения: 12.03.2026).



