Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Харченко В.И. 1, 2 Курбатов И.А. 1 Чередниченко А.И. 1, 2

---

1 ФГАОУ ВПО «Дальневосточный федеральный университет»

2 ФГБУН «Институт химии» ДВО РАН

С целью теоретического исследования эффекта дисперсионного взаимодействия на электронное строение димеров комплексов M2(Acr)6·(H2O)4 (M = Y, La) квантово-химическим методoм теории функционала плотности (DFT) изучены их геометрическая структура и электронные характеристики в основном состоянии. Показано, что учет дисперсионных поправок с помощью метода DFT-D3 позволяет получить более корректные геометрические характеристики молекулярных кластеров данных комплексов, при этом длины связей внутри лигандов практически не изменяются. Включение дисперсионного взаимодействия в схему расчета не приводит к значительному перераспределению электронной плотности в рассмотренных слабополярных молекулярных системах. При этом энергия ВЗМО возрастает, а НВМО снижается, энергетическая щель ВЗМО-НВМО уменьшается на 0,03 эВ. Увеличение ионного радиуса РЗЭ приводит к увеличению дисперсионного взаимодействия в системе. Таким образом, при квантово-химическом моделировании комплексов РЗЭ обязателен учет дисперсионного взаимодействия для корректного описания физико-химических свойств и технологических процессов.

Статья в формате PDF

642 KB

акрилат

полимер

иттрий

лантан

квантово-химические расчеты

теория функционала плотности

электронное строение

дисперсионные взаимодействия

1. Adamo C., Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model // J. Chem. Phys. – 1999. – Vol. 110, № 13. – P. 6158–6171.

2. Bukvetskii B.V., Petrochenkova N.V., Mirochnik A.G. Crystal structure and luminescence of europium(III) acrylate // J. Struct. Chem. – 2009. – Vol. 50, № 3. – P. 485–489.

3. Bukvetskii B.V., Petrochenkova N.V., Mirochnik A.G. Crystal structure and luminescence of terbium(III) methacrylate // J. Struct. Chem. – 2010. – Vol. 51, № 1. – P. 194–197.

4. Granovsky A.A. http://classic.chem.msu.su/gran/firefly.

5. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu / S. Grimme, J. Antony, S. Ehrlich, H. Krieg // J. Chem. Phys. – 2010. – Vol. 132, № 15. – 154104, P. 1–19.

6. Quantum Chemical Study of the Electronic Structure and Excited States of Yttrium Chelate Complexes / V.I. Kharchenko, L.N. Alekseyko, A.G. Mirochnik, P.A. Zhikhareva, A.I. Cherednichenko // Fund. Res. – 2013. – № 6, Part 4. – P. 901–905.

7. Kharchenko V.I., Cherednichenko A.I., Alekseyko L.N. A Quantum chemical study of hexamethylthiophosphoramide dimerization effect on the photoelectron spectrum // Fund. Res. – 2015. – № 2, Part 23. – P. 5094–5099.

8. Martin J.M.L., Sundermann A. Correlation consistent valence basis sets for use with the Stuttgart-Dresden-Bonn relativistic effective core potentials: The atoms Ga-Kr and In-Xe // J. Chem. Phys. – 2001. – Vol. 114, № 8. – P. 3408–3420.

9. General Atomic and Molecular Electronic-Structure System / M.W. Schmidt, K.K. Baldridge, J.A. Boatz, S.T. Elbert, M.S. Gordon, J.H. Jensen, S. Koseki, N. Matsunaga, K.A. Nguyen, S.J. Su, T.L. Windus, M. Dupius, J.A. Montgomery // J. Comp. Chem. – 1993. – Vol. 14, № 11. – P. 1347–1363.

10. Zhurko G.A., Zhurko D.A. Chemcraft 1.8 (b436). Available at: http://www.chemcraftprog.com (Accessed on July 02 2015).

Комплексы редкоземельных элементов (РЗЭ) представляют большой практический интерес для современных химических технологий и оптоэлектроники. Полимеризация комплексных соединений РЗЭ приводит к получению новых полимеров и композиций на их основе, полимерные звенья которых содержат эквивалент металла, что обеспечивает не только улучшение многих свойств, присущих мономерам, но и возникновение новых перспективных характеристик. Возможность гомо- и сополимеризации комплексов лантаноидов (III) позволяет получить светотрансформирующие полимеры с заданными свойствами, отличающимися от свойств низкомолекулярных аналогов. Например, установлено, что структура кристаллов акрилата европия (III) и метакрилата тербия (III) представлена бесконечными цепями комплексов РЗЭ, связанных водородными связями и ван-дер-ваальсовым взаимодействием, причем в структуру комплексов входят молекулы воды, участвующие в водородных связях внутри цепи и между бесконечными цепочками полиэдров [2, 3].

В связи с тем, что данные по пространственному и электронному строению полимеров комплексов РЗЭ крайне ограничены, изучение строения кластеров и исходных комплексных соединений очень актуально. Изучение физико-химическими методами особенностей геометрической структуры и электронного строения способствует описанию механизмов электронного возбуждения и фотохимических процессов в молекулярных системах данных классов, что продиктовано необходимостью создания новых наноструктурированных оптоэлектронных материалов для современных устройств мониторинга технологических процессов [6, 7].

Увеличение числа мономерных звеньев в полимерной цепи комплексов РЗЭ приводит к росту влияния дисперсионного взаимодействия, поэтому целью настоящей работы является теоретическое физико-химическое исследование эффекта дисперсионных взаимодействий на геометрическое и электронное строение комплексов M(Acr)₃·(H₂O)₂ (M = Y, La; Acr – акрилат-анион, CH₂CHCOO–).

Материалы и методы исследования

Квантово-химические расчеты геометрической структуры и электронного строения комплексов M(Acr)₃·(H₂O)₂ и M₂(Acr)₆·(H₂O)₄ проведены в вакуумном приближении методом теории функционала плотности (DFT) с гибридным обменно-корреляционным функционалом PBE0 [1] с помощью программных пакетов GAMESS-US (версия 05.12.2014) [9], FireFly (PC GAMESS) (v8.1, b9035) [4]. Для атомов иттрия и лантана использован Штутгартский псевдопотенциал и базис ECP28MWB(Y) и ECP46MWB(La) [8], для других атомов взят базис 6-31G(d,p). В качестве начального приближения при оптимизации геометрии использованы экспериментальные геометрические параметры комплекса европия(III) аналогичного состава [2]. Условие минимума энергии молекулы проверялось по гессиану. Дисперсионные энергетические поправки в основном состоянии комплексов учтены в рамках эмпирических соотношений Гримме с помощью метода DFT-D3 [5], который позволяет корректно учитывать межмолекулярное взаимодействие комплексных соединений и молекул растворителя. Результаты расчетов визуализировались с помощью программы Chemcraft 1.8 (b436) [10].

Результаты исследования и их обсуждение

Для проведения квантово-химического моделирования звена полимера геометрические параметры биметаллического фрагмента были взяты из экспериментальной геометрической структуры аналогичного комплекса европия (III), содержащей два иона РЗЭ, шесть акрилат-анионов и четыре молекулы воды. Установлено, что оптимизированные геометрические структуры комплексов Y₂(Acr)₆·(H₂O)₄ (I) и La₂(Acr)₆·(H₂O)₄ (II) подобны (рис. 1).

Акрилат-анионы в изоструктурных комплексах I и II можно разделить на два типа: бидентантные (Б), связанные с одним ионом РЗЭ (например, акрилат-анион с атомами углерода C₁–C₃), и бидентантно-мостиковые (БМ), связанные с двумя ионами РЗЭ (C₄–C₆).

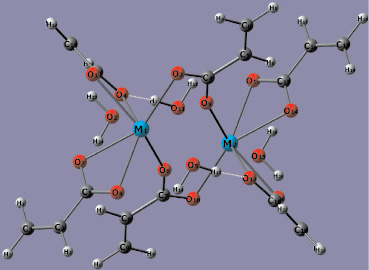
Рис. 1. Оптимизированная геометрическая структура комплексов М₂(Acr)₆·(H₂O)₄.

Таблица 1

Рассчитанные длины связей (Å), полная энергия Е_полн (а.е.) комплексов М₂(Acr)₆·(H₂O)₄

Примечание. а Δr = r(DFT-D3) – r(DFT), ΔЕ_полн = Е_полн(DFT–D3) – Е_полн(DFT).

Таблица 2

Рассчитанные заряды на атомах (по Малликену), дипольный момент µ (Д) и энергии ε_i (эВ) граничных MO комплексов М₂(Acr)₆·(H₂O)₄

Примечание. а Δq = q(DFT–D3) – q(DFT), Δµ = µ(DFT–D3) – µ(DFT); б Δε = ε(DFT–D3) – ε(DFT).

При учете дисперсионных поправок полная энергия системы понижается на 0,053 а.е. (I) и 0,049 а.е. (II), наибольшие изменения наблюдаются у длин связей металл-металл и металл-кислород, а связи внутри лигандов изменяются незначительно (табл. 1).

Очевидно, что при моделировании полимерных цепочек комплексов РЗЭ увеличение размера молекулярного кластера приведёт к росту дисперсионного взаимодействия, поэтому его учет необходим для получения корректных геометрических характеристик макромолекулярных систем комплексов РЗЭ.

Учет дисперсионного взаимодействия приводит к незначительному перераспределению электронной плотности в молекулярных системах I и II, причем заряд иона с меньшим ионным радиусом (иттрий) изменяется больше, как и длина связи металл-металл (табл. 2). Изменение дипольного момента в I и II также незначительно, поскольку рассмотренные системы характеризуются низкой полярностью, дипольный момент равен 0,003 и 0,008 Д соответственно.

Согласно проведенным расчетам, при учете дисперсионных поправок верхняя занятая молекулярная орбиталь (ВЗМО) (номер 142) дестабилизируется, а нижняя вакантная МО (НВМО) (143) стабилизируется, в результате чего разность энергий граничных МО уменьшается на 0,03 эВ для обеих систем (табл. 2).

При учете дисперсионного взаимодействия вклады атомных орбиталей (АО) акрилат-анионов в МО комплекса изменяются намного больше для комплекса II по сравнению с комплексом I (рис. 2). Включение дисперсионных поправок в схему расчета приводит к значительному перераспределению вкладов АО в МО и увеличивает вклады АО бидентантных акрилат-анионов в граничные МО комплексов. Большой рост вкладов АО бидентантно-мостиковых акрилат-анионов в НВМО приводит к её стабилизации. Таким образом, увеличение ионного радиуса РЗЭ связано с увеличением числа электронов и с ростом влияния дисперсионного взаимодействия в молекулярной системе.

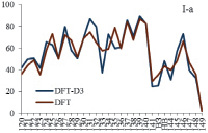
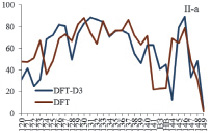
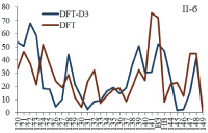
Рис. 2. Вклады АО бидентантных (а) и бидентантно-мостиковых (б) акрилат-анионов в МО (номера 120–149) комплексов М₂(Acr)₆·(H₂O)₄ (M = Y (I), La (II))

Выводы

Методом функционала плотности DFT/PBE0/ECPMWB в вакуумном приближении рассчитаны геометрическая структура и электронное строение комплексов иттрия и лантана М₂(Acr)₆·(H₂O)₄. Показано, что учет дисперсионных поправок в квантово-химических расчетах акрилатов данных РЗЭ позволяет получить более корректные геометрические характеристики комплексов, при этом длины связей внутри лигандов практически не изменяются. Включение дисперсионного взаимодействия в схему расчета не приводит к значительному перераспределению электронной плотности в рассмотренных слабополярных молекулярных системах. Энергия ВЗМО возрастает, а НВМО снижается, энергетическая щель уменьшается на 0,03 эВ. При квантово-химическом моделировании наноструктурированных молекулярных систем на основе комплексов РЗЭ для корректного описания физико-химических свойств и технологических процессов необходим учет дисперсионной поправки, поскольку увеличение ионного радиуса РЗЭ и рост размеров молекулярного кластера приводят к увеличению дисперсионного взаимодействия в системе.

Работа проводилась при финансовой поддержке «Стипендии имени Гензо Шимадзу» и Министерства образования и науки Российской Федерации в рамках государственного контракта № 2015/36 с Дальневосточным федеральным университетом (проект № 1137).

Рецензенты:

Кавун В.Я., д.х.н., заведующий лабораторией химической радиоспектроскопии, ФГБУН «Институт химии» ДВО РАН, г. Владивосток;

Мирочник А.Г., д.х.н., заведующий лабораторией светотрансформирующих материалов, ФГБУН «Институт химии» ДВО РАН, г. Владивосток.

Библиографическая ссылка