При моделировании переноса в мембранных системах в сверхпредельных токовых режимах обычно используются краевые задачи для системы уравнений Нернста – Планка и Пуассона [1–3, 5–10, 17].
В своих работах С.С. Духин и Н.А. Мищук [14], И. Рубинштейн [16] первыми дали теоретическое объяснение сверхпредельного тока электроконвекцией. Для этого они использовали двумерные уравнения Навье – Стокса для расчета течения раствора электролита и одномерные уравнения Нернста – Планка и Пуассона для расчета величины электрической силы. Аналогичные модели развивались в работах [11, 13, 19].
Использование приближенных решений краевых задач для одномерных, а не двумерных уравнений Нернста – Планка и Пуассона объясняется математическими сложностями исследования двумерных уравнений.
Впервые исследование электроконвекции на основе численного решения двумерной системы уравнений Нернста – Планка и Пуассона и Навье – Стокса проведено в работах [12, 15, 18] с некоторыми ограничениями на величины начальной концентрации, скорости протока раствора. Таким образом, возникает актуальная проблема асимптотического решения краевых задач для двумерных систем уравнений Нернста – Планка и Пуассона.
В работе [4] нами было получено асимптотическое представление для решения краевой задачи для двумерных систем уравнений НП с условием электронейтральности, удобное для сращивания с асимптотическим представлением в области пространственного заряда путем введения промежуточного слоя. В данной работе предлагается асимптотическое представление решения краевой задачи для двумерных систем уравнений Нернста – Планка и Пуассона в области пространственного заряда (ОПЗ).
Постановка задачи
1. Исходная система уравнений
Безразмерная система уравнений Нернста – Планка и Пуассона:
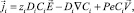 i = 1, 2; (1)
i = 1, 2; (1)
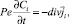 i = 1, 2; (2)
i = 1, 2; (2)
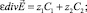 (3)
(3)
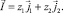 (4)
(4)
Асимптотическое представление в области пространственного заряда
1. Преобразование уравнений
Положим 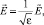
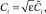 тогда
тогда
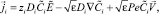 i = 1, 2;
i = 1, 2;
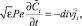 i = 1, 2;
i = 1, 2;
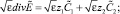
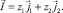
2. Асимптотическое упрощение
Полагаем 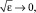
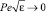 в преобразованных уравнениях, тогда получим
в преобразованных уравнениях, тогда получим
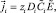 i = 1, 2; (5)
i = 1, 2; (5)
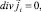 i = 1, 2; (6)
i = 1, 2; (6)
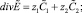 (7)
(7)
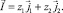
Из уравнения (6) следует, что потоки  , i = 1, 2, и, соответственно, плотность тока
, i = 1, 2, и, соответственно, плотность тока 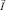 , соленоидальные вектора. Кроме того, поскольку в уравнения (5)–(7) время явно не входит, процесс переноса в ОПЗ в первом приближении является стационарным.
, соленоидальные вектора. Кроме того, поскольку в уравнения (5)–(7) время явно не входит, процесс переноса в ОПЗ в первом приближении является стационарным.
3. Преобразование системы упрощенных уравнений
Поделим уравнения (5) на Di, i = 1, 2, умножим на zi, i = 1, 2 и сложим, тогда
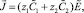 (8)
(8)
где 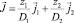 – некоторый соленоидальный вектор.
– некоторый соленоидальный вектор.
Уравнение (8) с учетом (7) примет вид
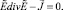 (9)
(9)
Уравнения для 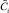 ,
, 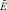 , не зависящие от неизвестных соленоидальных векторов
, не зависящие от неизвестных соленоидальных векторов  , i = 1, 2,
, i = 1, 2, 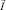 и
и  , можно получить, применив операцию div к обеим частям (5), (9):
, можно получить, применив операцию div к обеим частям (5), (9):
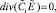 i = 1, 2; (10)
i = 1, 2; (10)
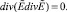 (11)
(11)
При решении системы уравнений (10), (11) возникают трудности в нахождении дополнительных краевых условий, т.к. порядок этих уравнений повысился. В связи с этим возникает проблема непосредственного решения уравнения (9).
Вывод уравнения для функции η
Рассмотрим условие разрешимости уравнения 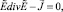 где
где  является соленоидальным вектором. Так как
является соленоидальным вектором. Так как  , соленоидальный вектор (т.е.
, соленоидальный вектор (т.е. 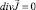 ), то существует такая функции η, что
), то существует такая функции η, что 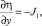
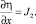
Введем оператор 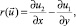 который является двумерным аналогом оператора rot, называется завихренностью и обладает следующими свойствами:
который является двумерным аналогом оператора rot, называется завихренностью и обладает следующими свойствами:
а) 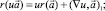
б) 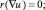
в) здесь 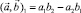 – кососимметричное скалярное произведение.
– кососимметричное скалярное произведение.
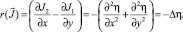 (12)
(12)
С другой стороны, с учетом 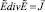 получим
получим
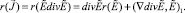
Так как 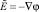 и
и 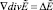 , то
, то 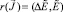 . Следовательно, для функции η получаем уравнение
. Следовательно, для функции η получаем уравнение
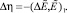 (13)
(13)
Уравнение (13) является условием разрешимости уравнения (9).
Таким образом, уравнение (9) эквивалентно системе уравнений
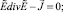
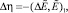
где 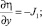
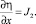
Преобразование системы уравнений (9), (13)
Из уравнения 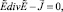 следует, что
следует, что 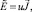 где u некоторая скалярная функция. Тогда
где u некоторая скалярная функция. Тогда
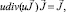
следовательно, 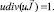 Так как
Так как
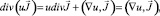
то для u получим уравнение 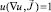 или
или 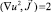 . Обозначим u2 = w, тогда для w получим уравнение
. Обозначим u2 = w, тогда для w получим уравнение 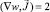 .
.
Преобразуем теперь уравнение
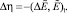
Заменим в уравнении 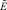 с учетом
с учетом 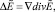
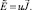 Кроме того, из
Кроме того, из
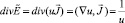
следует, что
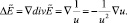
Таким образом, получаем уравнение
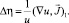
С учетом 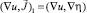 получим, что это уравнение запишется в виде
получим, что это уравнение запишется в виде
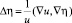 или
или 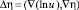 .
.
С учетом замены u2 = w получаем для функций w и η систему уравнений
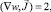 (14)
(14)
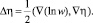 (15)
(15)
Замечание 1. Система уравнений (9), (13) может быть преобразована к виду (14), (15) и несколько другим способом.
Положим, 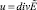 , тогда система уравнений запишется в виде
, тогда система уравнений запишется в виде
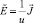 и
и 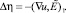
Здесь опять использовано равенство 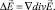
Заменим во втором уравнении 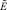 , тогда с учетом
, тогда с учетом 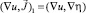 получим, что система этих уравнений запишется в виде
получим, что система этих уравнений запишется в виде
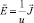 и
и 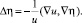
Для того чтобы вывести уравнение для u, найдем div от обеих частей первого уравнения, тогда
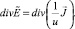
Откуда получаем уравнение для u:
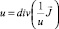 или
или 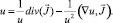
Так как 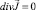 , то
, то 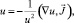 или, умножая обе части уравнения на u2, получим
или, умножая обе части уравнения на u2, получим 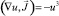 . Это уравнение является квазилинейным уравнением в частных производных первого порядка относительно u.
. Это уравнение является квазилинейным уравнением в частных производных первого порядка относительно u.
Таким образом, для двух функций u, η получим систему из двух уравнений:
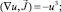
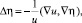
где 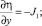
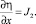 Систему уравнений
Систему уравнений
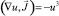 и
и 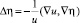
перепишем в виде
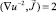 и
и 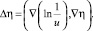
Полагая w = u–2, снова получим систему уравнений (14)–(15).
Замечание 2. Систему уравнений (9), (13) можно упростить и по-другому, если сделать замену 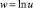 , тогда система уравнений запишется в виде
, тогда система уравнений запишется в виде
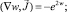 (16)
(16)
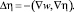 (17)
(17)
Методы решения системы уравнений (14), (15):
1. Метод простой итерации
Эту систему уравнений (14)–(15) можно решать, например, следующим методом последовательных приближений:
1. Пусть 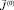 – некоторое начальное приближение к
– некоторое начальное приближение к  .
.
2. Определим w(0) как решение линейного уравнения переноса: 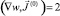 .
.
3. Определим η(0) как решение линейного уравнения:
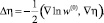
4. Определим 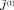 по формулам
по формулам
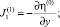
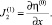
5. Проверим условие сходимости 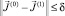 , где δ – заданная точность. Если условие сходимости выполняется, то принимаем
, где δ – заданная точность. Если условие сходимости выполняется, то принимаем 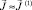 ,
, 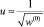 ,
, 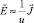 , иначе полагаем
, иначе полагаем  и идем к п. 2
и идем к п. 2
Замечание 3. Систему уравнений (16), (17) можно решать, например, методом последовательных приближений, аналогичным методу 5.1.
Метод линеаризации (Ньютона – Канторовича или Ньютона – Рафсона)
Систему уравнений (14), (15) можно решать методом линеаризации.
1. Пусть η(0), 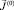 и w(0) некоторые начальные приближения к η,
и w(0) некоторые начальные приближения к η,  и w, причем
и w, причем
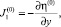
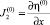 .
.
2. Определим η(1), 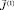 , w(1) как решения системы линейных уравнений
, w(1) как решения системы линейных уравнений
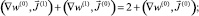
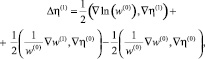
причем 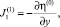
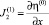 .
.
3. Проверим условие сходимости
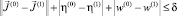 ,
,
где δ заданная точность. Если условие сходимости выполняется, то принимаем
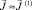 ,
, 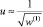 ,
, 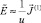 ,
,
иначе полагаем η(0) = η(1), w(0) = w(1) и идем к п. 2.
Замечание 4. Метод линеаризации можно применить и к системе уравнений (16), (17).
Замечание 5. Для конкретной реализации предложенных выше методов решения необходимо определить границы ОПЗ и соответствующие краевые условия. Эти проблемы можно решить путем использования различных физических гипотез, либо с использованием условий сращивания.
Заключение
В работе предлагается асимптотическое представление решения краевой задачи для двумерных систем уравнений Нернста – Планка и Пуассона в области пространственного заряда. Рассмотрены различные численные методы решения уравнений асимптотического представления, в том числе метод простой итерации и метод линеаризации. При моделировании различных явлений, например, электроконвекции, в первую очередь важно знать решение в области пространственного заряда. Полученные выше результаты можно использовать при решении таких задач. В то же время результаты этой работы совместно с результатами работы [4] дают асимптотическое представление решения краевой задачи для системы уравнений Нернста – Планка и Пуассона в основных областях, а именно в области электронейтральности и пространственного заряда.
Работа выполнена при финансовой поддержке РФФИ и администрации Краснодарского края, гранты: № 13-08-93106-НЦНИЛ_а и 13-08-96525 р_юг_а.
Рецензенты:
Халафян А.А., д.т.н., доцент, профессор, Кубанский государственный университет, г. Краснодар;
Павлова А.В., д.ф.-м.н., доцент, профессор, Кубанский государственный университет, г. Краснодар.
Библиографическая ссылка
Коваленко А.В. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ ДЛЯ СИСТЕМЫ УРАВНЕНИЙ НЕРНСТА – ПЛАНКА И ПУАССОНА В ОБЛАСТИ ПРОСТРАНСТВЕННОГО ЗАРЯДА // Фундаментальные исследования. 2015. № 9-1. С. 28-32;URL: https://fundamental-research.ru/ru/article/view?id=38960 (дата обращения: 14.03.2026).



