Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ромм Я.Е. 1 Чабанюк Д.А. 1

---

1 Таганрогский институт имени А.П. Чехова (филиал) ФГБОУ ВО РГЭУ (РИНХ)

В статье синтезированы параллельные алгоритмы построения двоичного дерева на основе параллельной и последовательной сортировок по матрицам сравнений. Даны три разновидности алгоритмов в конструктивной форме для множества из N элементов. Временная сложность построения двоичного дерева соответственно оценивается из соотношений T(R) = O(1), T(R) = O(log2N), где число процессоров R = (N2 – N)/2 и T(1) = O(log2N). Оценки получены на модели неветвящихся параллельных программ без учета операций обмена. Алгоритмы инвариантны относительно вида сортируемой по неубыванию последовательности, построение дерева выполняется со свойством единственности. Приводится пример работы параллельного алгоритма построения двоичного дерева с пошаговой интерпретацией процесса определения корней, ветвей и поддеревьев. Устанавливается взаимно однозначное соответствие двоичного дерева и отсортированной последовательности его элементов, а также возможность взаимного преобразования этих структур. Результаты ориентированы на создание эффективных методов динамической обработки баз данных.

Статья в формате PDF

915 KB

структуры данных

двоичные деревья

алгоритмы параллельных и последовательных сортировок

1. Акопов Р.Р. Двоичные деревья поиска // RSDN Magazine. – 2003. – № 5; url: http://rsdn.ru/article/alg/binstree.xml (дата обращения: 20.07.2015).

2. Axo А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы. – М.: Вильямс, 2003. – 384 с.

3. Вирт Н. Алгоритмы и структуры данных. – М.: ДМК Пресс, 2010. – 272 с.

4. Ромм Я.Е. Параллельная сортировка слиянием по матрицам сравнений. I // Кибернетика и системный анализ. – 1994. – № 5. – С. 3–23.

5. Ромм Я.Е. Параллельная сортировка слиянием по матрицам сравнений. II // Кибернетика и системный анализ. – 1995. – № 4. – С. 13–37.

6. Ромм Я.Е., Чабанюк Д.А. Параллельное построение декартова дерева с логарифмической оценкой временной сложности // Современные проблемы науки и образования. – 2015. – № 1; url: http://www.science-education.ru/121-18604 (дата обращения: 20.07.2015).

7. Солодовников В.И. Верхние оценки сложности решения систем линейных уравнений // В кн.: Теория сложности вычислений. I: Записки научных семинаров ЛОМИ АН СССР. – Л., 1982. – т. 118. – С. 159–187.

8. Kirkpatrick D.G., Przytycka T. Parallel Construction of binary trees with near optimal weighted path length // Algorithmica. – 1996. – Vol. 15. – Р. 172–192.

Древовидные структуры данных являются одними из наиболее распространенных в информатике и программировании, представляют собой иерархические структуры в виде набора связанных узлов. Такие структуры эффективны для представления динамических данных с целью быстрого поиска информации. Рост объемов обрабатываемой информации делает последовательное построение древовидных структур данных [2, 3] недостаточно эффективным, целесообразна разработка соответственных параллельных алгоритмов. В частности, актуальна задача синтеза и анализа параллельных алгоритмов построения двоичного дерева. Ниже параллельные алгоритмы рассматриваются на модели неветвящихся параллельных программ, временная сложность T(R) алгоритма (кратко – время выполнения) измеряется количеством последовательных шагов без учета обмена, R – число процессоров [7].

Предлагаемое решение задачи реализуется на основе алгоритмов параллельной сортировки.

Параллельная модификация сортировки подсчетом

Для построения двоичного дерева ко всем элементам массива данных будет применяться максимально параллельная сортировка подсчетом по матрице сравнений [5]. Модификация известного алгоритма заключается в следующем. Для одномерного массива a = (a1, a2, ..., an) сортируемых элементов составляется матрица сравнений, элемент αij которой определяется из соотношений

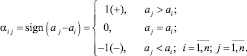
Пусть, например, требуется отсортировать по неубыванию массив a = (1, 0, –2, –4, 8, 2).

Матрица сравнений примет вид:

Входной элемент с номером j получает номер k в отсортированном массиве по правилу [5]: в j-м столбце матрицы подсчитывается количество нулей и плюсов сверху вниз до главной диагонали включительно и складывается с количеством только плюсов ниже диагонали в этом же столбце. Суммарное количество составит значение выходного номера k. Согласно данному правилу вставки получится

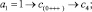
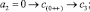
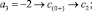
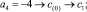
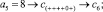
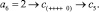
Отсортированный массив примет вид c = (–4, –2, 0, 1, 2, 8). Программа модифицированной сортировки представлена в [6] и частично приводится ниже.

При параллельной обработке все сравнения могут выполняться одновременно и взаимно независимо, требуемое количество процессоров составит 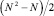. Отсюда временная сложность сортировки оценивается из соотношения

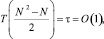(1)

где τ – время бинарного сравнения. Сортировка сохраняет порядок равных элементов, в явном виде задает взаимно однозначное соответствие входных и выходных индексов сортируемых элементов (адреса вставки: c[k]: = a[j]; адреса входных элементов в порядке расположения в отсортированном массиве: e[k]: = j;):

В приводимом ниже (пример 1) соотношении последовательностей (4) e[k] совпадает по значению и смыслу с ik. Использование входных индексов, записанных в e[k], позволит рассматриваемые в дальнейшем преобразования выполнять без перемещения элементов.

Параллельное построение двоичного дерева

Двоичное дерево – это структура данных, для которой выполняются следующие условия: оба поддерева – левое и правое – являются двоичными деревьями. У всех узлов левого поддерева произвольного узла X значения элементов меньше, нежели значение элементов самого узла X. В то же время значения элементов всех узлов правого поддерева (того же узла X) больше, нежели значение элементов узла X [1].

Пусть задано некоторое множество из N элементов Xi с отношением порядка ≤, расположенных в виде одномерного массива. Массив сортируется с помощью максимально параллельной сортировки за время (1). В качестве корня двоичного дерева выбирается серединный элемент отсортированного массива C с округлением индекса середины до ближайшего целого, не меньшего самого числа: 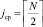. Тогда все элементы отсортированного массива слева от 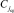меньше либо равны (не превосходят в смысле данного отношения порядка) 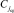, они автоматически определяются принадлежащими левому поддереву (левому подмассиву). Аналогично элементы справа от 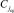не меньше (с сохранением порядка равных элементов) 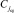и автоматически определяются как принадлежащие правому поддереву (правому подмассиву).

Далее, левый подмассив рассматривается как новый массив для аналогичного определения его корня по номеру

,

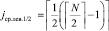или

.

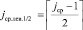Такой корень, 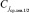, станет ближайшим слева потомком ранее найденного корня всего дерева 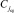, а также корнем левого поддерева. В силу сортировки левое поддерево с корнем 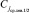сохраняет требуемые свойства: все элементы подмассива слева от 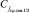не превосходят 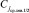(в смысле данного отношения порядка), все элементы подмассива справа, аналогично, не меньше .

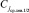Одновременно с левым правый подмассив рассматривается как новый массив для аналогичного определения его корня по номеру

,

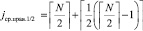или

.

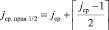Такой корень, 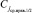, станет ближайшим справа потомком ранее найденного корня всего дерева 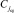, а также корнем правого поддерева. В силу сортировки правое поддерево с корнем 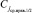сохраняет требуемые свойства: все элементы справа от 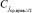не меньше 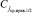(в смысле данного отношения порядка), все элементы слева не больше 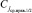. Далее, процесс итеративно повторяется по отношению к каждой паре смежных подмассивов слева и одновременно справа:

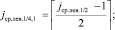
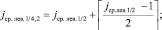
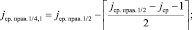
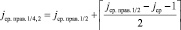и т.д.

Число шагов параллельного алгоритма построения двоичного дерева складывается из шага сортировки и последовательности параллельных шагов вычисления индексов корней поддеревьев, число которых равно целой части логарифма числа элементов входного множества:

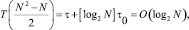(2)

где τ – время бинарного сравнения; τ0 – время вычисления индекса корня.

Пример 1. Двоичное дерево для массива из N = 15 элементов

X = (14, 9, 24, 7, 11, 20, 28, 3, 8, 10, 13, 17, 21, 25, 30) (3)

содержит уровни корней с номерами от 0 до .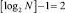

Поэтапно выполняется параллельная сортировка подсчетом по матрице сравнений массива (3), отсортированный массив C примет вид

C = (3, 7, 8, 9, 10, 11, 13, 14, 17, 20, 21, 24, 25, 28, 30). (4)

Корнем двоичного дерева является серединный элемент массива (4):

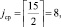C8 = 14

(сформирован 0-й уровень дерева).

Левый подмассив рассматривается как новый массив для аналогичного определения его корня, 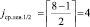, элемент C4 = 9 является ближайшим слева потомком корня 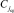и корнем левого поддерева. Одновременно правый подмассив рассматривается для аналогичного определения его корня, 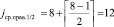, элемент C12 = 24 – ближайший справа потомок корня 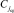и корень правого поддерева (сформирован 1-й уровень дерева). Далее, 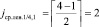, элемент C2 = 7 является ближайшим слева потомком ранее найденного корня поддерева 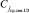, а также корнем левого от него поддерева. Одновременно смежный с левым правый подмассив рассматривается как новый массив для аналогичного определения его корня, 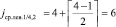, элемент C6 = 11 является ближайшим справа потомком корня поддерева 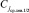, а также корнем правого от него поддерева. Аналогично левый подмассив от корня 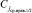правого поддерева рассматривается как новый массив для определения его корня, 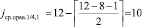, элемент C10 = 20 является ближайшим слева потомком корня поддерева 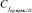, а также корнем левого от него поддерева. Для смежного с рассмотренным правого подмассива: 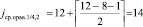, элемент C14 = 28 является ближайшим справа потомком корня поддерева 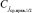, а также корнем правого от него поддерева (сформирован 2-й уровень дерева). Слева и справа от каждого из четырех найденных корней текущего уровня осталось по одному потомку, которые составят нижний уровень дерева (рисунок).

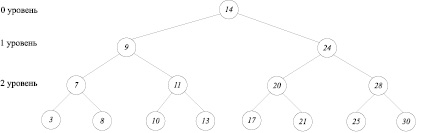
Пример построения двоичного дерева на основе модифицированной сортировки подсчетом

Таким образом, имеет место.

Лемма 1. Двоичное дерево для массива из N элементов может быть построено параллельно на основе модифицированной параллельной сортировки подсчетом по матрице сравнений с логарифмической оценкой временной сложности (2).

Очевидная модификация заключается в том, что индексы всех серединных элементов всех уровней могут быть вычислены за один шаг: для r-го уровня дерева эти индексы образуются как элементы последовательности 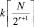, k = 1, 2, ..., r + 1, из которой исключаются индексы корней предшествующих уровней, .

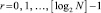Отсюда вытекает.

Теорема 1. Двоичное дерево для массива из N элементов может быть построено параллельно на основе рассматриваемой сортировки с единичной оценкой временной сложности (1).

Замечание 1. В силу устойчивости рассматриваемой сортировки, при условии округления до ближайшего целого не меньшего самого числа, в процессе вычисления индекса корня, двоичное дерево строится со свойством единственности.

Известен алгоритм последовательной сортировки слиянием по матрицам сравнений с явным заданием взаимно однозначного соответствия входных и выходных индексов сортируемых элементов [4], временная сложность которой T(1) = O(Nlog2N). Отсюда следует, что на одном процессоре с такой оценкой времени могут быть рассчитаны серединные элементы всех подмассивов.

Таким образом, справедливо следующее утверждение.

Теорема 2. Последовательное построение двоичного дерева для массива из N элементов может быть выполнено с временной сложностью O(Nlog2N).

Согласно изложенному можно утверждать, что двоичное дерево с единственностью строится на основе устойчивой сортировки, в явной форме задающей соответствие входных и выходных индексов сортируемых элементов. Вместе с тем верно и обратное: обход снизу вверх, слева направо элементов текущего поддерева, возобновляемый каждый раз при переходе от поддерева к предшествующему корню, влечет восстановление отсортированной последовательности. Так, например, для дерева на рисунке получится

3, 7 (корень), 8, 9 (корень), 10, 11 (корень), 13, 14 (корень), 17, 20 (корень), 21, 24 (корень), 25, 28 (корень), 30.

Очевидно, что процесс восстановления может быть максимально распараллелен.

Таким образом, между двоичным деревом и отсортированной последовательностью его элементов существует взаимно однозначное соответствие, которое в обе стороны реализуется конструктивным эффективно распараллеливаемым алгоритмом.

Заключение

В статье изложены разновидности алгоритмов построения двоичного дерева на основе устойчивой максимально-параллельной сортировки подсчетом. Временная сложность параллельного построения двоичного дерева в зависимости от разновидности представленных вариантов оценивается как 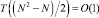, , 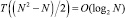что улучшает известные оценки [8], в последовательном варианте – T(1) = O(Nlog2N). На этой основе устанавливается взаимно однозначное соответствие двоичного дерева и отсортированной последовательности его элементов. Предложенные алгоритмы могут использоваться для создания эффективных методов динамической обработки баз данных.

Рецензенты:

Веселов Г.Е., д.т.н., директор Института компьютерных технологий и информационной безопасности, Инженерно-технологическая академия, Южный федеральный университет, г. Таганрог;

Карелин В.П., д.т.н., профессор, заведующий кафедрой прикладной математики и информационных технологий, Таганрогский институт управления и экономики, г. Таганрог.

Библиографическая ссылка