Важной частью производственного процесса электротехнических устройств являются системы автоматического управления производством, позволяющие повысить эффективность использования материалов и эксплуатационные параметры продукции [13]. Но никакая система управления производственным процессом не актуальна без эффективных методов диагностики.
Проведены исследования [4, 5, 8–10], подтверждающие, что вебер-амперная характеристика рабочего цикла является важной диагностической характеристикой электротехнических устройств, позволяющей определять не только их состояние, но и тип неисправности. Предложено для получения такой характеристики использовать решение обратной задачи гармонического баланса [2, 3, 14, 15]. Проведен математический анализ решения обратной задачи гармонического баланса, проведены вычислительный и натурный эксперименты с использованием математической модели и ряда электротехнических устройств (электромагнитного реле, электродвигателя и тороидального трансформатора), результаты которых позволяют утверждать, что предложенный метод измерения ВАХ, основанный на решении обратной задачи гармонического баланса, позволяет получить характеристику электротехнического устройства с погрешностью не превышающей 3 % [6]. Данный метод может быть использован для испытания электротехнических устройств как при их производстве, так и в ходе их эксплуатации.
В качестве еще одного метода определения вебер-амперных характеристик электротехнических устройств предложен метод натурно-модельных испытаний [7]. Для исследования данного подхода разработана программа, реализующая модель электротехнического устройства и оптимизационная программа на основе симплекс-планирования. Как и в случае с применением решения обратной задачи гармонического баланса, метод позволяет получить характеристику с погрешностью, не превышающей 3 %.
Проведено [7] исследование влияния погрешности измерения гармоник тока на точность методов определения вебер-амперных характеристик. Значения гармоник тока варьировались в интервале ±4,4 %, дополнительная погрешность получения вебер-амперных характеристик не превысила 1 %.
В ходе диагностики электротехнических устройств переменного тока зачастую необходимо получать гистерезисную вебер-амперную характеристику (ГВАХ).
При намагничивании магнитного материала переменным полем петля гистерезиса, характеризующая затраты энергии за один цикл перемагничивания, расширяется (увеличивает свою площадь) за счет возникновения потерь на вихревые токи и потерь на последействие. Такая петля называется гистерезисной [1].
Аналогичным образом вебер-амперная характеристика (ВАХ), полученная при перемагничивании переменным током, является гистерезисной ВАХ.
При измерении ГВАХ необходимо учитывать два явления: искажение формы кривой и сдвиг по фазе между магнитным потоком F и током в катушке I, создающим этот поток.
Зависимость между F и I определяется формой динамической петли, поэтому при синусоидальном изменении одной из рассматриваемых величин в общем случае вторая будет изменяться не синусоидально (появятся высшие гармоники). Одновременное синусоидальное изменение F и I возможно лишь в случае эллипсоидальной петли.
Отставание по фазе кривой потока от кривой тока объясняется действием вихревых токов и магнитной вязкостью. Угол отставания d называется углом потерь [12].
Для учета явлений искажения формы кривой и наличия сдвига по фазе в зависимости F = f(I) при намагничивании переменным полем В.К. Аркадьевым [1] было предложено заменить реальную динамическую петлю эквивалентным эллипсом, в случае ДВАХ уравнение которого в координатах F и I имеет вид
i(t) = Imax sin(ωt); (1)
F(t) = Fmaxsin(ωt – δ). (2)
Если ввести в составляющую потока Fmax1 = Fmax cosδ, совпадающую по фазе с направлением I, и составляющую Fmax2 = Fmax sinδ, отстающую на 90° от направления I, тогда [11] Fmax1 связана с обратимыми процессами превращения энергии при перемагничивании, а Fmax2 – с необратимыми. Выражение (2) примет вид
F(t) = Fmax1sin(ωt) – Fmax2cos(ωt). (3)
При магнитных измерениях в переменных полях [12] получают зависимости Вmax = f(Hmax) при одновременном измерении угла сдвига фаз δ между кривыми. Пользуются и другими зависимостями, например,
В1max = f(H1max),
где В1max, H1max – амплитудные значения первых гармоник.
Мы предлагаем метод определения петли F = f(I) + Fmax2cos(ωt), в котором учитывается ее гистерезисный характер.
Решение обратной задачи гармонического баланса позволяет определить форму петли F = f(I) + Fmax2cos(ωt), по известному протекающему через катушку электротехнического устройства току, заданному в виде разложения в ряд Фурье:
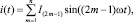(4)
где I(2m–1) – амплитуда (2m – 1)-й гармоники тока и по известной форме и амплитуда Ua напряжения приложенного к катушке электротехнического изделия:
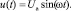(5)
Обратимая составляющая гистерезисной вебер-амперная характеристика электротехнического изделия, задана аппроксимирующим выражением
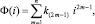(6)
где Ф – значение магнитного потока; k(2m–1) – коэффициенты аппроксимирующего выражения вебер-амперной характеристики,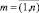 
; n – количество слагаемых в аппроксимирующем выражении; i – сила тока, протекающего через катушку электротехнического изделия.
Обратная задача гармонического баланса для определения гистерезисной вебер-амперной характеристики электротехнического устройства формируется следующим образом. Имеется электротехническое устройство с неизвестной гистерезисной вебер-амперной характеристикой, известны законы изменения напряжения (5), приложенного к нелинейной индуктивности, и протекающего по ней тока (4). Требуется определить коэффициенты k(2m–1) выражения (6), аппроксимирующего гистерезисную вебер-амперную характеристику и амплитуду необратимой составляющей потока Fmax2.
Запишем уравнение цепи электротехнического устройства:
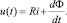
Перепишем его с учетом известных законов изменения тока (4) и напряжения (5):
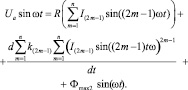(7)
Задавшись степенью (2n – 1) аппроксимирующего обратимую составляющую гистерезисной вебер-амперной характеристики выражения, определим n значений аргумента функции синуса для выражения (7). Значения аргумента берем из интервала ]0; π/2[.
Таким образом, получаем систему из n линейных уравнений. Для подстановки в полученную систему уравнений могут быть измерены: амплитуда напряжения Ua, амплитуды гармоник тока I(2m–1), значение активного сопротивления R и значение круговой частоты протекающего тока w. Решая эту систему уравнений, получаем коэффициенты k(2m–1) и амплитуду необратимой составляющей потока Fmax2.
Подводя итог, можно утверждать, что предложенный метод измерения ГВАХ, основанный на решении обратной задачи метода гармонического баланса, является актуальным для систем диагностики и его возможно использовать для получения гистерезисных магнитных характеристик электротехнических устройств.
Результаты работы получены при поддержке проекта № 1.2690.2014/K «Методы решения обратных задач диагностики сложных систем (в технике и медицине) на основе натурно-модельного эксперимента», выполняемого в рамках проектной части государственного задания с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ (НПИ).
Рецензенты:
Горбатенко Н.И., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова», г. Новочеркасск;
Ковалев О.Ф., д.т.н., профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.
Библиографическая ссылка
Ланкин А.М., Ланкин М.В., Гречихин В.В., Шайхутдинов Д.В. ОПРЕДЕЛЕНИЕ ГИСТЕРЕЗИСНЫХ МАГНИТНЫХ ХАРАКТЕРИСТИК МЕТОДОМ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ГАРМОНИЧЕСКОГО БАЛАНСА // Фундаментальные исследования. – 2015. – № 8-2. – С. 303-306;URL: https://fundamental-research.ru/ru/article/view?id=38890 (дата обращения: 18.04.2024).