Большую часть времени полета воздушно-космические аппараты находятся на большой высоте при свободномолекулярных условиях, и экспериментальное исследование при таких условиях весьма проблематично. И методы вычислительной аэродинамики разреженного газа в настоящее время являются практически единственным средством получения информации об аэродинамической ситуации в окрестности космического аппарата. Определение граничных условий на поверхности, обтекаемой разреженным газом, является одной из важнейших проблем кинетической теории газов [6]. Взаимодействие газа с поверхностью обтекаемого тела играет определяющую роль в высотной аэродинамике [1].
Метод прямого статистического моделирования (Монте-Карло) является наиболее распространенным среди численных методов решения прикладных задач динамики разреженного газа. Метод Монте-Карло широко применяется в аэродинамике как универсальный метод расчета тел сложной формы с учетом затенения. Более того, в последнее время явно прослеживается тенденция применения этого метода к расчету всего спектра течений – от сплошной среды до свободномолекулярного течения [2].
Целью настоящей работы является исследование аэродинамических характеристик (АДХ) аэрокосмических аппаратов методом прямого статистического моделирования (Монте-Карло) в высокоскоростном потоке разреженного газа. В работе рассматривается влияние модели взаимодействия молекул газа с поверхностью на АДХ аэрокосмических аппаратов.
Постановка задач свободномолекулярного обтекания
Основным инструментом исследования высотной аэродинамики аэрокосмических аппаратов является метод прямого статистического моделирования (Монте-Карло). Важным преимуществом метода прямого статистического моделирования (Монте-Карло) по сравнению с решением задачи на основе уравнения Больцмана является формулировка граничных условий в терминах вероятностного описания для каждой молекулы, а не в виде функции распределения в окрестности границы [2, 7].
Будем считать, что на границах области столкновения молекул между собой не играют существенной роли, что справедливо в случае Kn = l/L >> 1, т.е. когда длина пробега молекул газа l существенно превышает характерные размеры тела L. Тогда на границах области рассматриваемого течения функция распределения влетающих в область молекул будет равна f∞, которая, как показывает опыт, является максвелловской. Количество частиц, влетающих в область в единицу времени через все границы, будет равно
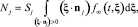
где Nj – поток частиц через границу с номером j; nj – единичный нормальный вектор; x – вектор скорости молекулы. Вычисление Nj сводится к известным интегралам от максвелловской функции, зависящим от скоростного отношения S (аналога числа Маха)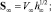 
h∞ = m/2kT∞ = 1/2RT∞, здесь V – скорость потока, k – постоянная Больцмана, R – универсальная газовая константа.
Модели взаимодействия молекул газа с поверхностью
Граничными условиями для уравнения Больцмана являются условия, связывающие функцию распределения падающих и отраженных молекул. Роль законов взаимодействия молекул с поверхностью проявляется тем сильнее, чем более газ разрежен [6]. В течение длительного времени использовалась схема зеркально-диффузного отражения Максвелла.
В модели Максвелла плотность распределения отраженных молекул имеет вид
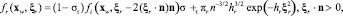
и ядро рассеяния [1, 6] имеет вид
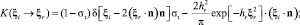
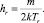
Здесь полагается, что доля (1 – σt) молекул отражается зеркально, а остальная часть σt молекул – диффузно, параметр 0 ≤ σt ≤ 1 определяет коэффициент аккомодации касательной компоненты импульса
σt = (Pti – Ptr)/Pti.
В модели CL (Черчиньяни – Лампис) ядро рассеяния для касательной к поверхности компоненты скорости имеет вид
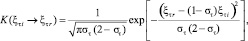
здесь ξti, ξtr – касательная к поверхности компонента скорости для падающей и отраженной молекул, отнесенная к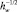 
.
Ядро рассеяния удовлетворяет принципу взаимности и условиям нормировки:
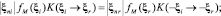
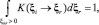
здесь fM – Максвелловская плотность распределения.
Использованное преобразование расширяет CL модель для учета обмена вращательной энергией между газом и поверхностью [8]. Модель в таком виде называется моделью Черчиньяни – Лампис-Лорда (CLL). Потом были предложены модификации модели [10] для учета обмена колебательной энергией и расширения диапазона состояний рассеянных молекул. Модель CLL в настоящее время получила широкое признание в работах [3, 9, 11, 13–15].
Результаты исследования и их обсуждение
Рассмотрим решение задач определения аэродинамических характеристик аэрокосмических аппаратов методом прямого статистического моделирования (Монте-Карло) в свободномолекулярном потоке разреженного газа. В работе используются различные модели взаимодействия молекул с поверхностью Максвелла и Черчиньяни – Ламписа – Лорда (CLL). Значения параметров: температурный фактор tw = Tw/T∞ = 0,04; 0,1; скоростное отношение S = 20; коэффициенты аккомодации тангенциального импульса и нормальной энергии στ , σn = 0,5; 0,75; 1. Расчет проводился с использованием 5·106 частиц.
На рис. 2 и 3 представлены зависимости коэффициентов силы сопротивления Cx, подъемной силы Cy, момента тангажа mz от угла атаки a от -90° до +90° для крылатого космического аппарата (рис. 1). При уменьшении στ от 1 до 0,5 величина Cx снижается до 1,85 при –55°< α < 55°, и при уменьшении στ от 1 до 0,75 величина Cx снижается до 1,74 при –55°< α < 55°. В рамках модели Максвелла при больших по модулю углах атаки зеркально отраженные молекулы повышают величину Cx, чего не наблюдается в рамках модели CLL.
Рис. 1. Геометрия крылатого космического аппарата
При уменьшении στ от 1 до 0,5 величина Cx увеличивается до 2,64 при α = +90°. Коэффициент Cy снижает в несколько раз по модулю при уменьшении στ от 1 до 0,5; 0,75. График mz(a) показывает, что при уменьшении στ наблюдается возрастание mz(a). Это можно объяснить тем, что при нулевой аккомодации (στ = 0) все молекулы отражаются зеркально, и при полной аккомодации отражаются диффузно (στ = 1). Зеркально отраженные молекулы передают поверхности больший импульс, чем диффузно рассеянные от холодной стенки молекулы [3].
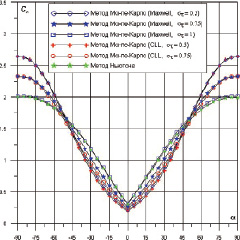
Рис. 2. Зависимости Cx(a) для крылатого космического аппарата (tw = 0,1)
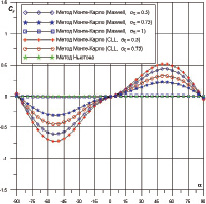
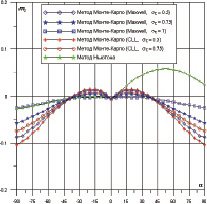
Рис. 3. Зависимости Cy(a) и mz(a) для крылатого космического аппарата (tw = 0,1)
Можно сказать, что величина нормальных и касательных напряжений, вызываемых отраженным потоком, зависит от характера отражения молекул. Отметим, что близость результатов, полученных с помощью моделей Максвелла и CLL, отмечалась ранее в работе [12] для тел с высокими коэффициентами аккомодации поверхности, что позволяло достигнуть лучшего согласования с результатами эксперимента в аэродинамической трубе.
На рис. 5 и 6 представлены зависимости коэффициентов силы сопротивления Cx, подъемной силы Cy, момента тангажа mz от угла атаки a при различных στ для спускаемого аппарата (рис. 4). Используются различные модели взаимодействия молекул с поверхностью (Максвелла и Черчиньяни – Лампис – Лорда, CLL). Значения параметров: температурный фактор tw = Tw/T∞ = 0,04; 0,1; скоростное отношение s = 20; коэффициенты аккомодации тангенциального импульса и нормальной энергии στ , σn = 0,5; 1; угол атаки a = 0–30°.
Рис. 4. Геометрический вид спускаемого аппарата
Коэффициент Cx уменьшается с ростом угла атаки α до значения около 1,89 при α = 30° при στ = 1. При уменьшении στ от 1 до 0.5 величина Cx увеличивается до 2,72 при α = 0°. Коэффициент Cy снижает в несколько раз по модулю при уменьшении στ от 1 до 0,5. Зависимость mz(a) объясняет то, что при понижении στ чувствительно увеличивает в рамках разных диапазонов углов атаки.
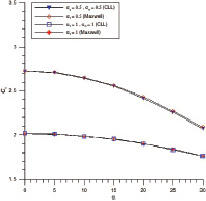
Рис. 5. Зависимости Cx(a) при tw = 0,04 для спускаемого аппарата
При (σt, σn = 0, 1) значительно совпадали [4, 5, 16]. Но при малых углах атаки отраженные молекулы слабо отклоняются от первоначального направления и поэтому вносят малый вклад в сопротивление тонкого тела. При дальнейшем увеличении угла атаки ситуация изменяется: зеркально отраженные молекулы передают поверхности конуса больший импульс, чем диффузно рассеянные от стенки молекулы.
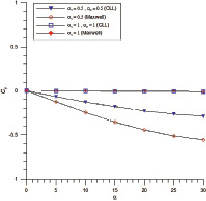
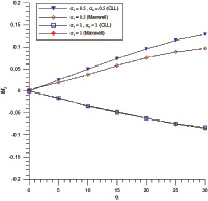
Рис. 6. Зависимости Cy(a) и mz(a) при tw = 0,04 для спускаемого аппарата
Заключение
Представлены результаты расчетов аэродинамических сил сопротивления Cx, подъемной силы Cy, момента тангажа mz аэрокосмических аппаратов методом Монте-Карло при различных значениях коэффициентов аккомодации st, sn с использованием различных моделей взаимодействия молекул с поверхностью (Максвелла и CLL). Исследовано влияние на АДХ особенностей модели взаимодействия молекул с поверхностью. Результаты сравнены с традиционным методом Ньютона. Разработанные программные системы позволяют оперативно получать АДХ разрабатываемых и эксплуатируемых на орбите и на начальном участке траектории спуска космических аппаратов и могут быть использованы при проектировании перспективных космических систем.
Работа выполнена при поддержке РФФИ (Грант № 14-07-00564-а).
Рецензенты:
Хлопков Ю.И., д.ф.-м.н., профессор, ФГУП «Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского», г. Жуковский;
Шалаев В.И., д.ф.-м.н., профессор, факультет аэромеханики и летательной техники, Московский физико-технический институт (государственный университет), г. Жуковский.
Библиографическая ссылка
Зея Мьо Мьинт ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ВЫСОТНОЙ АЭРОДИНАМИКИ АЭРОКОСМИЧЕСКИХ АППАРАТОВ // Фундаментальные исследования. – 2015. – № 7-4. – С. 749-754;URL: https://fundamental-research.ru/ru/article/view?id=38814 (дата обращения: 20.04.2024).