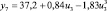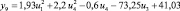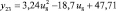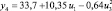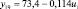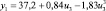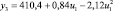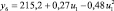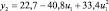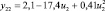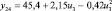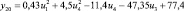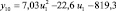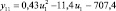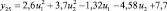Важнейшей составляющей в общем комплексе мероприятий по повышению надежности систем вентиляции и кондиционирования воздуха (СВ и КВ) объектов космической инфраструктуры является совершенствование процесса их эксплуатации, в частности технического обслуживания. Но эффективная организация технического обслуживания невозможна без информации о фактическом техническом состоянии оборудования, т.е. без проведения контроля и диагностирования. Необходимы разработка и внедрение современного методического и аппаратурного обеспечения получения объективной информации о состоянии СВ и КВ.
Цель исследования заключается в построении математической модели диагностирования как основы методики диагностирования СВ и КВ по параметрам основных рабочих процессов.
Исходные предположения и допущения метода исследования
Для разработки математического и методического обеспечения диагностирования СВ и КВ применены как методы параметрической статистики для определения допустимых пределов изменения контролируемых признаков (КП) на нижележащих уровнях иерархии системы, так и методы теории распознавания образов. Указанные методы позволяют формировать изображения видов технического состояния СВ и КВ, соответствующие отказам подсистем и функциональных элементов (ФЭ) посредством реализации процедуры обучения при отсутствии сведений о законе распределения значений КП.
В ходе исследований по каждому виду технического состояния СВ и КВ получена обучающая выборка
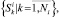
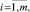 (1)
(1)
а координаты eij изображений выражены как среднее арифметическое соответствующих координат элементов выборки
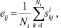 eij ∈ [–1, 1],
eij ∈ [–1, 1],
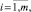
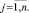 (2)
(2)
Разработка модели
Применение выражения (2) позволяет получить изображения
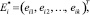
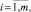
которые наилучшим образом (с точки зрения достоверности диагностирования) описывают свойства каждого вида ТС.
Кроме того в работе предложен способ уточнения изображений на основе процедуры дообучения посредством использования дополнительной диагностической информации
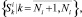 (3)
(3)
где 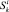 в выборке (3) – дополнительные обучающие образы, полученные на этапе эксплуатации системы контроля и диагностирования.
в выборке (3) – дополнительные обучающие образы, полученные на этапе эксплуатации системы контроля и диагностирования.
Адаптированное (уточненное) изображение i-го вида технического состояния СВ и КВ определяется выражением
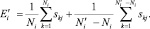 (4)
(4)
Решающие правила, применяемые в теории распознавания образов, для задач контроля и диагностирования СВ и КВ в исходном виде неприменимы. Необходима их доработка с учётом особенностей целевого содержания указанных задач и применяемых методов распознавания. Выделяются два метода распознавания – комбинационный и последовательный. При комбинационном распознавании решение принимается на основе анализа результатов всех проверок из заданного множества, которые могут выполняться в произвольном порядке. При последовательном распознавании соблюдается некоторая очерёдность выполнения проверок.
Для каждого из рассматриваемых методов распознавания разработаны решающие правила. При диагностировании СВ и КВ последовательным методом указанное правило имеет вид
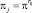 , если
, если 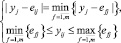 (5)
(5)
или
где  – исход проверки;
– исход проверки; 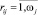 ; yj – текущее значение j-го контролируемого признака; eij – j-я координата изображения i-го вида ТС.
; yj – текущее значение j-го контролируемого признака; eij – j-я координата изображения i-го вида ТС.
Преимущество решающего правила (5) перед известными в том, что оно инвариантно к физической природе характеристик выходных процессов СВ и КВ. Это обеспечивает возможность унификации описания процесса принятия решений о ТС любого объекта из состава СВ и КВ.
Предложено формальное описание последовательности выполнения проверок КП, в рамках которого процесс диагностирования рассматривается как случайный эксперимент.
Если в качестве эффективности рассматриваемого процесса принимается достоверность решений о ТС, соотнесённая с затратами динамических ресурсов, то в качестве показателя эффективности может быть принята средняя вероятность ED получения правильного решения с учётом ограничений на указанные виды ресурсов. Оптимизационная задача в данном случае заключается в нахождении упорядоченных подмножеств πi ⊆ П, 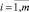 , таких, что
, таких, что
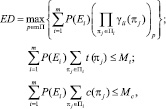 (6)
(6)
где P(Ei) – вероятность i-го вида ТС; γii(πj) – величины, определяемые через вероятности ошибок первого и второго рода j-й проверки; Mt, Mc – максимально допустимые расходы временного и трудового ресурсов соответственно; t(πj), c(πj) – затраты времени и трудовых ресурсов на выполнение j-й проверки; mП – множество перестановок на множестве проверок.
Средняя вероятность принятия правильного решения о техническом состоянии СВ и КВ находится из выражения
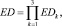 (7)
(7)
где EDk – средняя вероятность принятия правильного решения на k-м уровне.
При этом справедливы выражения
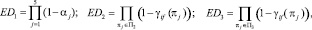 (8)
(8)
где αj – вероятность ошибки первого рода j-й проверки; П2, П3 – множество проверок КП на втором и третьем уровнях; βj – вероятность ошибки второго рода j-й проверки;
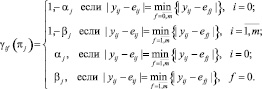
В целях формирования обучающей выборки о работоспособном состоянии СВ и КВ были проведены экспериментальные исследования на лабораторном образце кафедры «Системы жизнеобеспечения объектов наземной космической инфраструктуры» ВКА имени А.Ф. Можайского. Математическая модель диагностирования (поиска отказов) разработана как с использованием обучающей выборки о работоспособном состоянии СВ и КВ, так и экспериментальных данных по отказам. Посредством машинной реализации процесса обучения построены изображения всех видов технического состояния СВ и КВ в виде векторов числовых величин. При этом использовались как экспериментальные данные, так и обучающие образы, полученные путём имитационного моделирования. На множестве видов ТС задано дискретное распределение вероятностей. Определены регрессионные зависимости КП второго уровня от входных воздействий этого же уровня СВ и КВ, функционирующей в режиме фильтровентиляции (табл. 2).
Таблица 1
Математическая модель контроля работоспособности СВ и КВ
|
№ п/п |
Регрессионная зависимость yj = f(ui) |
Вычисленное значение F |
Критическое значение F |
|
1 |
|
95,6 |
6,1 |
|
2 |
|
101,2 |
5,8 |
|
3 |
|
37,2 |
6,1 |
Таблица 2
Регрессионные зависимости КП от входных переменных для СВ и КВ, функционирующей в режиме фильтровентиляции
|
№ п/п |
Регрессионная зависимость yj = f(ui) |
Вычисленное значение F |
Критическое значение F |
|
1 |
|
95,6 |
6,1 |
|
2 |
|
110 |
5,4 |
|
3 |
|
540 |
6,1 |
|
4 |
|
210 |
6,1 |
|
5 |
|
123 |
6,1 |
|
6 |
|
245 |
6,1 |
|
7 |
|
225 |
6,1 |
|
8 |
|
54 |
6,1 |
|
9 |
|
101,2 |
5,8 |
|
10 |
|
211 |
6,1 |
|
11 |
|
140 |
6,1 |
|
12 |
|
150 |
5,8 |
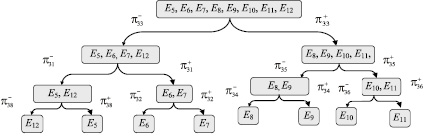
Рис. 1. Гибкая программа диагностирования системы специальной фильтровентиляции (третий уровень)
На основе полученных результатов построена гибкая программа диагностирования на третьем уровне иерархии (рис. 1), оптимальная по критерию максимума средней вероятности получения правильного решения о техническом состоянии СВ и КВ. При разработке программы реализовывалось решающее правило (5). Данная программа представляет собой составную часть модели, но одновременно является выходным документом по организации диагностирования, т.е. методическим обеспечением указанных работ.
На основе изложенной последовательности определения технического состояния СВ и КВ и её реализации на оборудовании конкретного типа разработана блок-схема методики контроля и диагностирования (рис. 2). Она отражает все этапы подготовки исходных данных, их обработки, построения математического обеспечения, проверки его адекватности и принятия решений о техническом состоянии СВ и КВ, а также взаимосвязь этих этапов между собой. Применение методики для контроля и диагностирования СВ и КВ на других объектах космической инфраструктуры требует реализации только части этапов по формированию обучающей выборки о работоспособном состоянии СВ и КВ и вычислению коэффициентов регрессии. Необходимость в построении второго и третьего уровней модели, определении структуры уравнений регрессии отпадает.
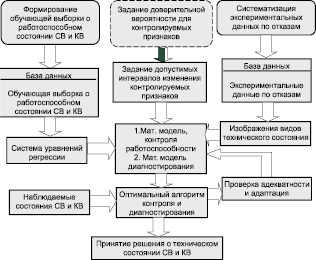
Рис. 2. Блок-схема методики контроля и диагностирования систем вентиляции и кондиционирования воздуха
Выводы
В принятом подходе к построению моделей учитывается случайный характер появления отказов СВ и КВ. В связи с этим на множестве видов ТС используется дискретное распределение вероятностей.Для получения решений о техническом состоянии СВ и КВ необходима разработка таких программ диагностирования, которые описывают последовательность логических условий и переходов в процессе принятия решений. Выполнена формализация последовательности выполнения проверок КП и сформулирована общая постановка задачи оптимизации процесса принятия решений о техническом состоянии СВ и КВ. Сформирована структура целевой функции и ограничений на ресурсы при оптимизации по критерию максимума средней вероятности принятия правильного решения о техническом состоянии СВ и КВ.
Рецензенты:
Сеньченков В.И., д.т.н. профессор, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург;
Авсюкевич Д.А., д.т.н., профессор, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Библиографическая ссылка
Некрасов И.Н., Моторин В.М., Глуханов А.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИАГНОСТИРОВАНИЯ СИСТЕМ СПЕЦИАЛЬНОЙ ФИЛЬТРОВЕНТИЛЯЦИИ // Фундаментальные исследования. 2015. № 7-2. С. 343-347;URL: https://fundamental-research.ru/ru/article/view?id=38698 (дата обращения: 06.03.2026).