Многообразие конструкций, компоновок, достаточно обширный научный потенциал выполненных исследований, в большей степени отдельных, частных случаев, требует единого подхода к созданию механизмов позиционирования автоматизированного производства научного анализа, синтеза и управления такими механизмами. Преимущества имеют механизмы позиционирования с оптимальным управлением позиционными циклами на основе мехатронных модулей. В этих условиях следует иметь в виду быстроходные механизмы позиционирования, выполняющие как отдельные движения, так и сложные позиционные циклы, длительность которых определяется не только временем движения Тц, но и быстродействием формирования команд на переключение управлений SТу, передачи управления на последующие движения (на замедление Тзм, установлено скорости позиционирования Ту и остановка Тпоз). В этом случае Тц = SТi, что характеризует быстроходность механизма. При этом необходимо учитывать ограничения по точности перемещения ∆L ≤ │∆L max│. Установление влияния величины и характера изменения кинематических и силовых параметров в процессе позиционирования позиционного пневматического привода является целью нашего исследования. Объектом исследования является механизм перемещения схвата пневматического робота.
Автоматизированное технологическое оборудование имеет замкнутые рабочие циклы, формируемые следующими движениями: быстрый подвод, замедление, остановка c позиционированием, быстрый отвод. Эффективность работы привода определяется длительностью рабочего цикла и точностью переключения элементов рабочего цикла. Они обеспечивают требования повышенного быстродействия и точности позиционирования исполнительных движений. Обобщенные траектории исполнительных движений целевых механизмов представлены на рис. 1.
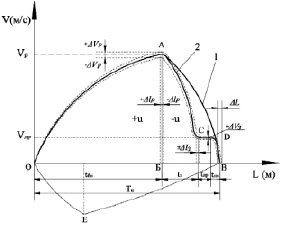
Рис. 1. Типовые траектории исполнительных движений целевых механизмов: 1 – обобщенная траектория исполнительного движения; 2 – оптимальная траектория движения
Точки О, В фиксируют конечные положения выходного звена объекта управления. В зависимости от резерва мощности привода возможны различные траектории. В обычных оптимальных позиционных приводах – «ступенчатую» ОACDB, в быстроходных позиционных – «колокол» ОАВ. Последняя обеспечивает минимальное время перемещения и называется оптимальной (ОА – разгон, АВ – торможение). Она получена решением задачи оптимального быстродействия; точка О – исходное положение (стоп) с фиксацией выходного звена привода; V0 = 0, Lп = 0 – структура привода с перекрытым сливом; участка О-А – разгон автоматизированного пневмопривода (АПП) до скорости Vбп по траектории Lбп; в точке А – переключение управления u1 на замедление АПП; участка А-В – замедление АПП до торможенной скорости Vдр; C-D – участок перед торможением с Vдр; В точке D – переключение управления u2 на остановке АПП; в точке B: переключение управления на реверсировании движения. Время рабочего хода определяется выражением
TЦ = tбп + tз + tдр + tпз, (1)
где TЦ – время позиционного цикла; tбп – время быстрого подвода; tз – время замедления до скорости позиционирования Vдр; tдр – время до торможения; tпз – время остановки с позиционированием.
Таким образом, организация и исполнение рабочих циклов в реальном пространстве и времени требует автоматизированного управления его параметрами: перемещение, положение ΔL, скорость V, сила F, организация рабочего цикла. Во многих случаях необходимо управление их отклонениями. Необходимо принять ограничения по точности и быстродействию привода ТЦ → min, ∆lз ≤ │∆lз max │ и ∆L ≤ │∆L max│. В такой постановке оптимальная траектория получается решением задачи оптимального быстродействия [1, 3]. Основным направлением поиска технического решения являлись программные позиционные пневмоприводы с внешним тормозом, наиболее полно отвечающие поставленной задаче, обеспечивающей структурно-параметрическое управление рабочим циклом и позиционированием позиционного пневмопривода.
Принципиальная пневмокинематическая схема обобщенной структуры АПП представлена на рис. 2. Она определяет состав устройств, пневмомеханические связи. При одновременном включении электромагнитов YА1, YА5 распределитель Р1 переключается в левую позицию, воздух через обратный клапан попадает в поршневую полость силового пневмоцилиндра ПЦ1. При включении электромагнита YА5 воздух попадает в многофункциональный датчик. Шток силового пневмоцилиндра ПЦ1 начинает выдвигаться, при этом рейка, жёстко связанная со штоком, вращает вал датчика. Сигнал датчика, представляющий собой импульсы давления, попадает на датчик давления (ДД), с которого в виде электрических импульсов поступает в систему управления (ПЛК). При достижении определённого положения включается YА3, происходит переключение распределителя Р3, скорость движения штока цилиндра ПЦ1 уменьшится до скорости, задаваемой дросселем Др2. В заданной точке включается электромагнит YA4, подаётся давление в цилиндры тормоза (ПЦ2 и ПЦ3), шток останавливается.
Повышенные требования к технологическому оборудованию по точности и быстродействию обусловливают необходимость проведения оценки их динамического качества уже на этапе проектирования. При этом существенно сокращается время последующих испытаний и улучшается качество рабочих процессов реальных позиционных пневматических приводов при меньших затратах времени и средств.
На основе принципов и правил математического описания динамических подсистем с механическими связями, обоснованных работами [2, 4, 5], получена математическая модель, которая представляет систему нелинейных дифференциальных уравнений, описывающих поведение ее подсистем в процессе позиционных перемещений. Были приняты следующие допущения:
● модель считается одномассовой;
● характеристики источника питания рн = const, Tн = const, поскольку напорная магистраль пневмопривода соединена с ресивером достаточного объема через регулятор давления;
● процесс изменения состояния газа в пневмосистеме считается адиабатическим, поскольку процесс позиционирования происходит за короткий промежуток времени;
● рабочее тело пневматического устройства – воздух рассматривается как идеальный газ, процессы в котором описываются уравнением Клайперона – Менделеева, поскольку давление в пневмосистеме ниже 10 бар;
● утечки в подвижных соединениях малы, они зависят главным образом от конструктивного исполнения и могут быть ограничены коэффициентом утечки Kу.
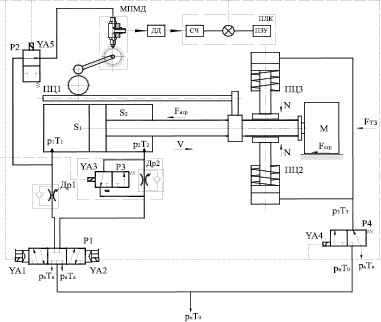
Рис. 2. Принципиальная пневмокинематическая схема АПП: ДД – датчик давления; ПЛК – программируемый логический контроллер; ПЗУ – программируемое задаваемое управление; ПЦ1 – силовой пневмоцилиндр; ПЦ2, ПЦ3 – тормозные пневмоцилиндры; Р1, Р2, Р3, Р4 – пневмораспределители; Др1, Др2 – дроссели с обратным клапаном; М – перемещаемая масса
1. Уравнение движения привода.
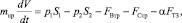 (2)
(2)
где S1, S2 – эффективная площадь поршневой и штоковой полостей пневмоцилиндра соответственно, м2; p1, p2 – давление воздуха соответственно в поршневой и штоковой полости пневмоцилиндра, Па; V – скорость перемещения движущихся масс, м/с; kВт – коэффициент вязкого трения, Н∙с/м; mпр – масса подвижных частей привода; 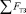 – сила трения, создаваемая приводом тормоза, Н; FТЗ = λFН; FН – усиления на штоке, Н; α = 0 при t < tТЗ и α = 1 при t ≥ tТЗ; tТЗ – задаваемое время начала процесса торможения; x – перемещение штока силового пневмоцилиндра; FСтр = FТО·sign(V) – сила сухого трения, Н; FВтр = kВтV – сила вязкого трения, Н; kВт – коэффициент вязкого трения.
– сила трения, создаваемая приводом тормоза, Н; FТЗ = λFН; FН – усиления на штоке, Н; α = 0 при t < tТЗ и α = 1 при t ≥ tТЗ; tТЗ – задаваемое время начала процесса торможения; x – перемещение штока силового пневмоцилиндра; FСтр = FТО·sign(V) – сила сухого трения, Н; FВтр = kВтV – сила вязкого трения, Н; kВт – коэффициент вязкого трения.
Уравнение (2) можно написать в следующем виде:
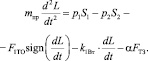 (3)
(3)
2. Уравнения давлений в АПП.
Из условия неразрывности потока газа для средних значений параметров газа по сечению пневмораспределителей: G = const, где G – массовый расход сжатого воздуха, fp = π·d·x – площадь сечения пневмораспределителя.
– Уравнение баланса массового расхода напорной линии силового пневмопривода.
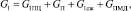 (4)
(4)
где 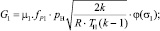
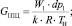
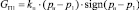 ;
;
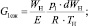
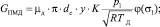
G1 – массовый расход напорной линии м3·с–1; G1ПЦ – массовый расход в бесштоковой полости силового пневмоцилиндра, м3·с–1; GП – массовый расход, идущий на перетечки рабочий воздух, м3·с–1; G1сж – сжимаемость массового расхода воздуха напорной линии, м3·с–1; kп – коэффициент перетечки рабочего воздуха; GПМД – массовый расход, протекающий через пневмомеханический датчик, м3·с–1; pд – давление в рабочей зоне пневмомеханического датчика, Па; dc – диаметр сопла, м; у – расстояние между соплом и диском.
Уравнение (5) имеет следующий вид:
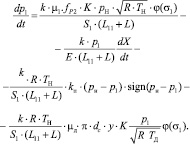 (5)
(5)
– Уравнение баланса массового расхода сливной линии силового пневмопривода.
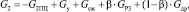 (6)
(6)
где 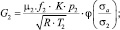
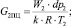
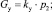
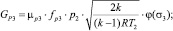
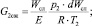
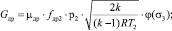
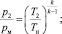 G2 – массовый расход сливной линии, м3·с–1; G2ПЦ – массовый расход в штоковой полости силового пневмоцилиндра, м3·с–1; Gу – массовый расход, идущий на утечки рабочего воздуха, м3·с–1; G2сж – сжимаемость массового расхода воздуха сливной линии, м3·с–1; GР3 – массовый расход через пневмораспределитель Р3, м3·с–1; Gдр – массовый расход через пневмодроссель Др2, м3·с–1;
G2 – массовый расход сливной линии, м3·с–1; G2ПЦ – массовый расход в штоковой полости силового пневмоцилиндра, м3·с–1; Gу – массовый расход, идущий на утечки рабочего воздуха, м3·с–1; G2сж – сжимаемость массового расхода воздуха сливной линии, м3·с–1; GР3 – массовый расход через пневмораспределитель Р3, м3·с–1; Gдр – массовый расход через пневмодроссель Др2, м3·с–1; 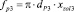 – площадь сечения полости пневмораспределителя Р3, м2;
– площадь сечения полости пневмораспределителя Р3, м2; 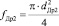 – площадь сечения полости пневмодросселя Др2, м2; dР3 – диаметр сечения полости пневмораспределителя Р3, м; dДр2 – диаметр сечения полости пневмодросселя Др2, м; Рм – давление питания, Па.
– площадь сечения полости пневмодросселя Др2, м2; dР3 – диаметр сечения полости пневмораспределителя Р3, м; dДр2 – диаметр сечения полости пневмодросселя Др2, м; Рм – давление питания, Па.
Уравнение (5) имеет следующий вид:
 (7)
(7)
где 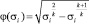 при 0,528 < σi < 1; φ(σi) = 0,2588 при 0 < σi ≤ 0,528;
при 0,528 < σi < 1; φ(σi) = 0,2588 при 0 < σi ≤ 0,528; 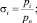
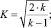 k – показатель адиабаты (для воздуха k = 1,4); Тм, TД, T2 – температура воздуха питания, в пневмомеханическом датчике, на сливной линии; Pм, Ра, Р1, Р2 – давление питания, атмосферы, воздуха соответственно в нагнетательной и выхлопной магистралях, Па; fР2, fР3 – площади проходных сечений пневмораспределителей, м2; fДр2 – площадь проходного сечения дросселя, м2; s – ход пневмоцилиндра; μ1, μ2, μ3, μДр2 – коэффициенты расхода; L11, L12 – отношение начальных («пассивных») объемов Wн, Wсл пневмопривода к полезной площади поршня поршневой и штоковой полостей пневмоцилиндра соответственно, м; W1, W2 – объемы пневмоцилиндра ПЦ1 к площади поршня поршневой и штоковой полостей м3; x0ТЗ – отношение начальных («пассивных») объемов пневмопривода к площади отверстия распределителя Р4 (рис. 1), м; R – универсальная газовая постоянная (R = 287 Дж/(кг·К));
k – показатель адиабаты (для воздуха k = 1,4); Тм, TД, T2 – температура воздуха питания, в пневмомеханическом датчике, на сливной линии; Pм, Ра, Р1, Р2 – давление питания, атмосферы, воздуха соответственно в нагнетательной и выхлопной магистралях, Па; fР2, fР3 – площади проходных сечений пневмораспределителей, м2; fДр2 – площадь проходного сечения дросселя, м2; s – ход пневмоцилиндра; μ1, μ2, μ3, μДр2 – коэффициенты расхода; L11, L12 – отношение начальных («пассивных») объемов Wн, Wсл пневмопривода к полезной площади поршня поршневой и штоковой полостей пневмоцилиндра соответственно, м; W1, W2 – объемы пневмоцилиндра ПЦ1 к площади поршня поршневой и штоковой полостей м3; x0ТЗ – отношение начальных («пассивных») объемов пневмопривода к площади отверстия распределителя Р4 (рис. 1), м; R – универсальная газовая постоянная (R = 287 Дж/(кг·К)); 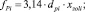 E – модуль объемной упругости смеси жидкости и воздуха, Па; kп – коэффициент перетечки.
E – модуль объемной упругости смеси жидкости и воздуха, Па; kп – коэффициент перетечки.
3. Уравнение управляющих золотниковых пневморапределителей [4, 5].
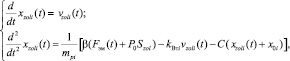 (8)
(8)
где электромагнитная сила рассчитывается по формуле
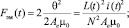
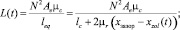
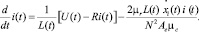
При постоянном токе i(t) = 20 мА и напряжении U(t) = 24 В; N – число оборотов катушки; xзазор – общий воздушный зазор, м; Ae – эффективная площадь поперечного сечения пути потока, м2; xzol(t) – перемещение золотника, м; μc, μ0 – проницаемость сердечника; θ – магнитный поток; μr – относительная проницаемость сердцевины; mpi – масса золотника перемещения, кг; Szol – площадь пневмораспределителя, к которым относятся P0, м; С – коэффициент жёсткости пружины, Н/м; kВmi – коэффициенты вязкостей; i = 1, 3, 4; β – булевой параметр.
4. Модель пневмомеханического тормоза
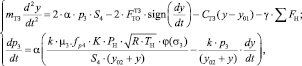 (9)
(9)
где mТЗ – перемещаемая масса тормозного устройства; y – путь торможения; р3 – давление в бесштоковой полости тормозного цилиндра; S4 – площадь тормозной колодки; СТЗ – коэффициент жёсткости пружины пневмоцилиндра тормоза, Н/м; FТЗ = λ·FН – сила трения, Н; FH – нормальная сила; λ – коэффициент трения; γ – булевой параметр.
Система нелинейных дифференциальных уравнений (2)–(9) может решаться различными численными методами (Эйлера, Рунге – Кутты и др.) при заданных начальных условиях. Исследование предлагаемой модели выполнено с использованием программной поддержки Matlab-Simulink 2012b численным методом Рунге – Кутты.
Моделирование проводилось при следующих исходных данных: перемещаемая масса подвижных частей привода mпр = [10, 12, 15, 17] кг; диаметр поршня силового пневмоцилиндра D = 0,06 м; диаметр штока силового пневмоцилиндра d = 0,04 м; коэффициенты расхода μ1 = 0,6; μ2 = 0,8; μ3 = 0,4; коэффициент упругости пружины распределителей Ci = 100 Н/м; давление питания Pн = 6·105 Па; атмосферное давление ра = 1·105 Па; k = 1,4; ход силового пневмоцилиндра s = 0,284 м; температура ТН = Тп = Ta = 290 K; R = 287; N = 1000 об; диаметр золотника dzol = 0,002 м; Ae = 0,75·10–4 м2; μ0 = 4·pi·10–7; μr = 120·10–6; xzolimax = 0.008(м); λ = 0,42. При начальных условиях: t = 0 → (X(0), V(0), P1(0), P2(0), xzol2(0), vzol3(0), xzolimax, vzol2(0)) = (0; 0, 0; 6e5; 0; 0; 0,002; 0).
При t = tпб → (Xпб; Vmax; P1(tпб); P2(tпб); xzol2max; 0; 0,002; 0).
При моделировании позиционных циклов более подробно исследовались участки позиционирования Lпоз (перехода с Vбп на скорость позиционирования привода).
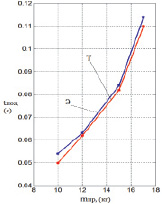
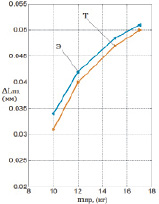
На рис. 3 представлены результаты моделирования процесса замедления движения АПП с установленной скоростью Vбп до скорости позиционирования Vпоз = 0,2 м/с, с длиной хода 0,284 м. Команда на замедление подается в координатах Lпб. Команда на остановку подается в координате L = 0,284 м. Колебательности переходного процесса на участке позиционирования отметим удовлетворительность каждого из них по основным критериям оценки устойчивости (колебательного перерегулирования, допустимая погрешность 5 %). При этом максимальное ускорение торможения достигается 7,2 м/с2, не превышается допустимое ускорение на удар (< 8 м/с2). Длину участка позиционирования Lпз определяла величина перемещения АПП от координаты, в которой падается команда управления на замедление до координаты АПП остановки. На рис. 4 представлены результаты вычислений и экспериментов исследования влияния перемещаемых масс АПП на участке позиционирования и точность позиционирования. При удовлетворительности совпадения результатов вычислений и натурных экспериментов установлено их существенное влияние на длительность, быстродействие участка и точность позиционирования. Так при изменении перемещаемых масс m от 10 до 17 кг время, длительность на участке позиционирования увеличивается в 1–1,8 раза и точность позиционирования увеличивается в 1,75 раз и точность позиционирования не превышает 0,051 мм.
Предложена и исследована обобщенная математическая модель динамической позиционной пневматической системы привода горизонтального перемещения робота, позволяющая описывать динамику переходных процессов на участке позиционирования. Вычислительным и натурным экспериментами на стенде-модели подтверждается адекватность предлагаемой модели с удовлетворительным совпадением моделируемых процессов. Установленные зависимости величины и длительности участка позиционирования от перемещаемых масс позволяют определять зоны устойчивого позиционирования по времени и точность позиционирования исследованиями достигается быстродействия АПП превышающие в 1–1,8 раза, результаты известных аналогов при точности позиционирования (0,031–0,051 мм) в исследованном диапазоне перемещаемых масс (10–17 кг).
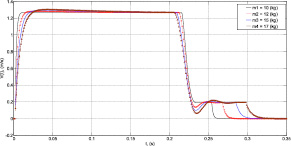
Рис. 3. Динамика позиционного цикла при различных перемещаемых массах mпр: mпр = 10 кг; mпр = 12 кг; mпр = 15 кг; mпр = 17 кг
 а
а 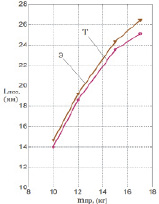 б
б
 в
в
Рис. 4. Влияние перемещаемых масс mпр, (кг) на участке позиционирования и на точность позиционирования АПП при вычислении (Т) и экспериментом (Э) исследования: а – время участка позиционирования; б – длина участка позиционирования; с – точность позиционирования АПП
Рецензенты:
Шошиашвили М.Э., д.т.н., профессор, заведующий кафедрой «Мехатроника и гидропневмоавтоматика», ФГБОУ ВПО «Южно-Российский государственный технический университет», г. Новочеркасск;
Шишкарев М.П., д.т.н., доцент, заведующий кафедрой «Информационное обеспечение автоматизированных технологических комплексов», ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону.
Библиографическая ссылка
Дао Тхе Ань, Сидоренко В.С. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ПОЗИЦИОНИРОВАНИЯ БЫСТРОДЕЙСТВУЮЩЕГО ПНЕВМОПРИВОДА РОБОТА // Фундаментальные исследования. 2015. № 7-2. С. 285-292;URL: https://fundamental-research.ru/ru/article/view?id=38687 (дата обращения: 14.02.2026).



