Руководителям региона при принятии решения о развитии отраслей экономики обычно приходится иметь дело с большим количеством информации, характеризующей социально-экономическое развитие региона. Для уменьшения времени на формирование и принятие решений, руководителям необходимо предоставить визуализированные материалы («шаблоны для принятия решений»). Одним из направлений формирования таких «шаблонов» является использование результатов прогнозирования состояния экономики с помощью количественного или качественного исследования динамической системы, которая моделируется при помощи системы дифференциальных уравнений. Для количественного анализа могут использоваться стандартные методы численного интегрирования. Естественно, во многих случаях количественный анализ более удобен и оперативен. Но при принятии решений у руководителя может не быть возможности, желания и времени для интегрирования системы дифференциальных уравнений при ограниченном лимите времени, отведенного на принятие решения. Кроме этого, у руководителя должны быть навыки программирования и применения методов численного интегрирования. Поэтому для формирования визуализированных «шаблонов» рекомендаций предлагается использовать результаты качественного исследования динамической системы [1, 5]. Таким образом, необходимо провести анализ поведения фазовой траектории экономики ХМАО-Югры в целом с помощью анализа проекций фазовой траектории экономики на фазовые плоскости.
Анализ поведения проекций фазовой траектории на фазовые плоскости
Исследования, проводимые в рамках данной статьи, являются логическим продолжением исследований, приведенных в [7]. В соответствии с результатами факторного анализа экономики ХМАО-ЮГРЫ, проведенного в [6], рассматривалось влияние на параметр TEPI (индекс «Добыча топливно-энергетических полезных ископаемых») следующих параметров:
TEKS (индекс «Текстильное и швейное производство»);
MASH (индекс «Производство машин и оборудования»).
В данной статье рассматривается анализ проекций фазовых траекторий в «смежных» плоскостях, при этом общей для всех таких плоскостей будет являться ось TEPI. Исходные данные для построения проекций фазовых траекторий приведены в таблице. Для составления таблицы использованы данные с сайтов www.gks.ru и [2]. На рис. 1–2 приведены проекции фазовых траекторий, построенные с использованием данных из таблицы. Точка № 1 на рис. 1–2 соответствует началу 2011 года, точка № 2 – началу 2012 года, точка № 3 – началу 2013 года, точка № 4 – началу 2014 года, точка № 5 – началу 2015 года и точка № 6 – концу марта 2015 года.
На рис. 1 приводится проекция фазовой траектории динамической системы на плоскость «TEPI – добыча топливно-энергетических полезных ископаемых» – «TEKS-текстильное и швейное производство». Из рис. 1 видно, что наблюдается наличие областей притяжения движения (выделены прямоугольниками). Первой, «негативной» области притяжения соответствуют диапазоны значений индексов 97–99 по параметру TEPI и 80–93 по параметру TEKS. Следует отметить, что проекция фазовой траектории возвращается в данную область притяжения в течение 2011–2012 годов. Затем в течение 2013 года следует выход из области притяжения в «негативные» для индекса TEPI точки «3» и «U». После этого проекция фазовой траектории попадает в «позитивную» область притяжения, характеризующуюся диапазонами значений индексов 102–105 по параметру TEPI и 110–150 по параметру TEKS. В данной области проекция фазовой траектории находится в течение полугода. Точка «3» (точка, в которой достигается максимальное значение индекса TEKS) и точка «U» (точка, в которой достигается минимальное значение индекса TEPI) представляют собой точки экстремума проекции фазовой траектории.
Исходные данные для построения проекций фазовых траекторий
|
Год |
Месяц |
TEPI |
TEKS |
MASH |
Год |
Месяц |
TEPI |
TEKS |
MASH |
|
2011 |
Январь |
98,60 |
93,10 |
108,60 |
2013 |
Январь |
91,70 |
230,00 |
123,40 |
|
Февраль |
98,20 |
57,60 |
109,60 |
Февраль |
94,00 |
182,50 |
124,00 |
||
|
Март |
97,70 |
61,20 |
113,60 |
Март |
88,80 |
167,50 |
137,30 |
||
|
Апрель |
97,50 |
47,70 |
112,40 |
Апрель |
90,60 |
151,80 |
121,10 |
||
|
Май |
97,30 |
48,90 |
112,40 |
Май |
94,00 |
150,80 |
114,80 |
||
|
Июнь |
97,30 |
51,80 |
112,20 |
Июнь |
99,70 |
140,00 |
116,00 |
||
|
Июль |
97,20 |
57,00 |
109,90 |
Июль |
102,20 |
132,00 |
115,90 |
||
|
Август |
97,20 |
61,10 |
108,60 |
Август |
101,60 |
127,20 |
112,20 |
||
|
Сентябрь |
97,10 |
70,10 |
108,90 |
Сентябрь |
102,70 |
132,50 |
113,70 |
||
|
Октябрь |
96,90 |
71,30 |
106,20 |
Октябрь |
103,00 |
123,80 |
111,90 |
||
|
Ноябрь |
97,00 |
72,50 |
104,20 |
Ноябрь |
103,90 |
121,20 |
110,10 |
||
|
Декабрь |
97,00 |
77,10 |
102,60 |
Декабрь |
105,10 |
120,90 |
110,30 |
||
|
2012 |
Январь |
97,80 |
99,50 |
69,20 |
2014 |
Январь |
107,40 |
66,30 |
92,10 |
|
Февраль |
99,40 |
150,30 |
78,30 |
Февраль |
110,90 |
84,30 |
83,20 |
||
|
Март |
98,70 |
120,70 |
66,50 |
Март |
114,00 |
118,10 |
85,70 |
||
|
Апрель |
98,70 |
121,70 |
64,90 |
Апрель |
116,60 |
112,00 |
90,50 |
||
|
Май |
98,40 |
109,20 |
60,80 |
Май |
117,90 |
102,20 |
99,00 |
||
|
Июнь |
98,50 |
102,30 |
61,10 |
Июнь |
116,70 |
109,80 |
101,00 |
||
|
Июль |
98,40 |
95,50 |
62,50 |
Июль |
114,10 |
108,70 |
104,30 |
||
|
Август |
98,10 |
90,20 |
64,80 |
Август |
109,40 |
115,80 |
104,90 |
||
|
Сентябрь |
97,90 |
80,40 |
63,80 |
Сентябрь |
109,10 |
114,50 |
104,20 |
||
|
Октябрь |
97,50 |
79,90 |
64,10 |
Октябрь |
108,40 |
107,70 |
104,40 |
||
|
Ноябрь |
97,60 |
86,60 |
66,00 |
Ноябрь |
107,00 |
106,90 |
103,80 |
||
|
Декабрь |
97,70 |
84,60 |
71,30 |
Декабрь |
104,10 |
107,40 |
101,80 |
||
|
2015 |
Январь |
101,60 |
118,60 |
84,70 |
|||||
|
Февраль |
101,80 |
146,20 |
94,40 |
||||||
|
Март |
98,90 |
91,30 |
106,80 |
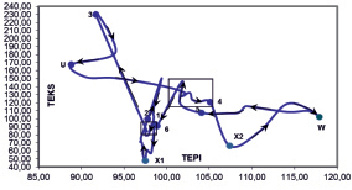
Рис. 1. Проекция фазовой траектории на плоскость «TEPI-TEKS»
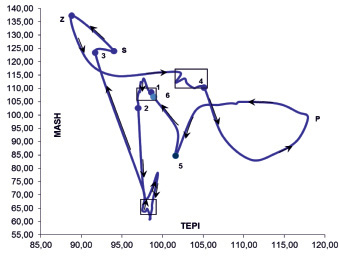
Рис. 2. Проекция фазовой траектории на плоскость «TEPI-MASH»
После прохождения проекции фазовой траектории через точку экстремума «U» направление движения проекции фазовой точки вдоль оси TEPI изменяется на противоположное. Аналогично, при прохождении проекции фазовой траектории через точку экстремума «3» направление движения проекции фазовой точки вдоль оси TEKS изменяется на противоположное. При этом на рис. 1 имеются и точки экстремума, характеризующиеся минимальными значениями индекса TEKS (точки «Х1» и «Х2»). При этом в 2013–14 годах наблюдается попадание проекции фазовой траектории в область притяжения, которая является «позитивной», с точки зрения значения индекса TEPI. В 2014 году проекция фазовой траектории достигает «позитивной» для индекса TEPI точки экстремума «W» (в которой достигается максимальное значение TEPI), делает возле нее петлю, проходит через «позитивную» область притяжения и в марте 2015 года достигает «негативной» области притяжения, соответствующей 2011–2012 годам. На рис. 1 в первой области возможно наличие кратной точки равновесия с координатами приблизительно (97, 86). Проекция фазовой траектории несколько раз проходит в пределах малой окрестности данной точки в течение 2011 и 2012 года, но не задерживается в ней. Первая область притяжения является крайне неблагоприятной для экономики региона. Попадание фазовой траектории в данную область приведет к уменьшению значения индекса добычи топливно-энергетических полезных ископаемых, а также к уменьшению индекса текстильного и швейного производства. Во второй области возможно наличие точки равновесия с координатами приблизительно (102, 120). Для экономики региона является очень хорошим вариантом наличие такой кратной точки равновесия, так как значения индексов TEPI и TEKS больше 100 %. По внешним признакам поведения проекции фазовой траектории в окрестности данных точек их можно классифицировать как сложные состояния равновесия в виде седловых либо седлоузловых точек [1, 4, 5]. Точки равновесия данного типа характеризуются тем, что проекции фазовой траектории не задерживаются в их малой окрестности. Точки типа «фокус» и «узел» (в малую окрестность которых проекции фазовой траектории стремятся и при этом остаются далее в малой окрестности) отсутствуют в данной фазовой плоскости.
Вторая проекция фазовой траектории строится на фазовой плоскости «TEPI – добыча топливно-энергетических полезных ископаемых» – «MASH – производство машин и оборудования» (рис. 2).
В 2011 году наблюдается область притяжения, в пределах которой проекция фазовой траектории находится в течение 6 месяцев. Первой области притяжения соответствуют диапазоны значений индексов 97–99 по индексу TEPI и 105–110 по индексу MASH. Данная область ограниченно приемлема для экономики региона. При этом если проекция фазовой траектории будет входить в данную область «сверху», то происходит уменьшение значения параметра MASH, хотя оно всё равно остается благоприятным для региона. При этом попадание проекции фазовой траектории в эту область приводит к уменьшению добычи топливно-энергетических полезных ископаемых вследствие того, что значение параметра меньше 100 %. Внутри данной области может находиться сложная точка равновесия с приблизительными координатами (98, 107). В соответствии с [1, 3, 4, 5] эту точку можно классифицировать как седлоузел. В 2012 году фазовая траектория также имеет область притяжения со значениями 97–99 по индексу TEPI и 61–66 по индексу MASH. В такой области проекция фазовой траектории находилась в течение 7–8 месяцев. Данная область «негативна» и неприемлема для развития экономики региона (значения индексов TEPI и MASH в данной области меньше 100 %). Очевидно, что попадание в такую область происходит при входе проекции фазовой траектории «сверху» (как это и происходит на рис. 2). Внутри данной области может находиться сложная кратная точка равновесия с приблизительными координатами (98, 63). В соответствии с [1, 3, 4, 5] эту точку можно классифицировать как седлоузел. В конце 2012 года происходит резкий «выброс» из «депрессивной» для экономики области притяжения. При этом в 2013 году проекция фазовой траектории достигает сначала точки «Z» (в которой одновременно достигается минимальное значение TEPI и максимальное значение MASH, рис. 2). После прохождения через точку экстремума проекция фазовой точки меняет направление движения вдоль осей TEPI и MASH на противоположное. Аналогичный резкий «выброс» характерен и для рассмотренной ранее фазовой плоскости «TEPI-TEKS» (точки «3» и «U», рис. 1). Далее динамика поведения проекции фазовой траектории характеризуется наличием позитивной для экономики региона области притяжения со значениями 102–106 по индексу TEPI и 110–116 по индексу MASH. Вход в данную область обеспечивает значения индексов TEPI и MASH более 100 %. Попадание в такую область позитивно для экономики региона. Внутри данной области проекция фазовой траектории находится 6 месяцев. Данная область притяжения может содержать сложную точку равновесия с приблизительными координатами (103, 111). В соответствии с [1, 3, 4, 5] эту точку также можно классифицировать как седлоузел. О кратности данной точки равновесия пока что судить трудно. В 2014–2015 годах также, по аналогии с фазовой плоскостью «TEPI-TEKS также происходит «выброс» в точку экстремума «P» (в которой значение индекса TEPI достигает максимального значения) и формирование «петли» для перемены направления движения проекции фазовой точки в противоположную сторону вдоль оси TEPI. После этого в марте 2015 года происходит вход проекции фазовой траектории в область притяжения, соответствующую 2011 году (так же, как и в фазовой плоскости «TEPI-TEKS»). Поэтому по аналогии с 2011 годом в 2015 году вероятен выход в крайне неблагоприятную для экономики региона область притяжения, соответствующую 2012 году.
По результатам анализа фазовых траекторий можно составить следующие «шаблоны для принятия решений»:
1. Для того чтобы значение индекса TEPI находилось в диапазоне от 102 % до 105 %, должно быть следующее сочетание значений индексов отраслей, позитивно влияющих на значение индекса TEPI:
– Текстильное и швейное производство – 122–140 %.
– Производство машин и оборудования – 110–116 %.
2. Если значение индекса TEPI находится в диапазоне 88–94 %, и при этом значения индексов отраслей, позитивно влияющих на значение индекса TEPI, принимают значения:
– Текстильное и швейное производство – 167–230 %,
– Производство машин и оборудования – 125–137 %,
то ожидается рост значения индекса TEPI с последующим превышением значения 100 %.
Заключение
В результате анализа фазовой траектории экономики региона обнаружены области притяжения фазовой траектории, попадание в которые приводит к различным вариантам развития экономики региона с точки зрения значения индекса добычи топливно-энергетических полезных ископаемых. Установлены области притяжения, обеспечивающие как благоприятные, так и неблагоприятные условия для экономики региона. Установлено, что в рассмотренных фазовых плоскостях проекции фазовой траектории в 2015 году возвращаются в области притяжения, не являющиеся благоприятными для экономики региона. В фазовых плоскостях обнаружены экстремальные точки, при прохождении через которые проекция фазовой точки меняет направление движения вдоль соответствующих осей координат на противоположное. При этом экстремальные точки первого типа характеризуются минимальным значением индекса TEPI, а экстремальные точки второго типа характеризуются максимальным значением индекса TEPI. Сформированы «шаблоны для принятия решений», которые предназначены для сокращения времени, затрачиваемого руководителями региона, на принятие решений по развитию экономики региона.
Рецензенты:
Титов В.А., д.э.н., профессор, профессор кафедры информационных технологий, ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова», г. Москва;
Курченков В.В., д.э.н., профессор, заведующий кафедрой государственного и муниципального управления, ФГАОУ ВПО «Волгоградский государственный университет», г. Волгоград.
Библиографическая ссылка
Попов А.А. АНАЛИЗ ПОВЕДЕНИЯ ФАЗОВОЙ ТРАЕКТОРИИ ЭКОНОМИКИ ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ В 2011–2015 ГОДАХ // Фундаментальные исследования. 2015. № 6-3. С. 602-606;URL: https://fundamental-research.ru/ru/article/view?id=38667 (дата обращения: 11.03.2026).



