В технических приложениях большое значение имеют задачи по определению осредненных по области значений физических параметров, например тепловой эффективности [4], потерь тепла [12], тепловой производительности теплообменников [1], термоупругих напряжений [2] и т.д. Для этого созданы специальные методы, например схема Ловерье [4, 12], метод «сосредоточенной емкости» [1, 2] и др. Однако при использовании этих методов возникают проблемы определения погрешностей физических параметров или приближенного детального описания полей в области осреднения.
В работах [5–8] и [10–11] показано, что такие задачи могут быть успешно решены на основе асимптотического метода при специальном выборе формального параметра асимптотического разложения. Применение этого метода к задачам сопряжения областей, в одной из которых преобладает конвективная теплопроводность, и его сущность на примере известной задачи Коши рассмотрены в монографии [9]. Там же описан случай применения формального параметра в квазистационарной задаче теплообмена, где рассмотренный метод асимптотического разложения приводит к точному решению в ограниченном числе слагаемых разложения.
В данной статье демонстрируется поэтапное решение нестационарной задачи теплообмена восходящего цилиндрического потока флюида, окруженного сплошным массивом и сравнение полученных асимптотических выражений с коэффициентами разложения точного решения в ряд Маклорена.
Параметризация. Для простоты математическая постановка задачи о температурном поле в вертикальной трубе с учетом адиабатического эффекта в восходящем потоке представлена в безразмерных переменных [11]
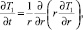 r > 1, t > 0; (1)
r > 1, t > 0; (1)
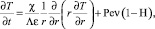
0 < r < 1, t > 0; (2)
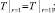
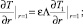 (3)
(3)
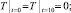
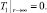 (4)
(4)
В задаче (1)–(4) введен параметр асимптотического разложения e формальной заменой L на e×L. Устремление e к 0 соответствует возрастанию радиальной теплопроводности до бесконечности, что приводит к выравниванию температурного фронта по r в области от 0 до 1.
Разложение по асимптотическому параметру. Для получения асимптотических решений задачу (1)–(4) представим в виде асимптотической формулы по параметру ε
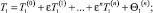
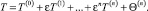 (5)
(5)
Подставляя (5) в (1)–(4), запишем разбитую по степеням параметра ε задачу
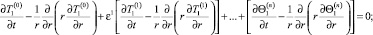 (6)
(6)
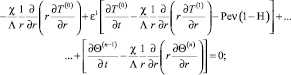 (7)
(7)
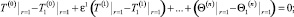
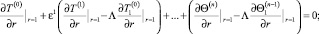 (8)
(8)
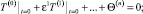
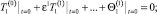
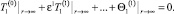 (9)
(9)
Из задачи (6)–(9) можно выписать постановку для любого из коэффициентов асимптотического разложения при одинаковых степенях параметра асимптотического разложения. Однако уравнение (7) и условие (8) содержат соседние коэффициенты разложения при одинаковых степенях ε и в этом смысле являются «зацепленными».
Расцепление задачи для нулевого коэффициента разложения. Приравнивая коэффициент e к нулю из (7), получим выражение
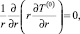
интегрируя которое с учетом условия (8) и требования ограниченности решения на бесконечности, определяем, что нулевой коэффициент асимптотического разложения температуры в области 0 < r < 1 не зависит от радиальной координаты. Используя этот факт, запишем «зацепленное» выражение из (7) при первой степени коэффициента асимптотического разложения в виде
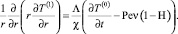 (10)
(10)
Интегрируя (10) с использованием условий (8), получим уравнение, содержащее только нулевые коэффициенты разложения
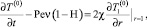
0 < r < 1, t > 0.
Постановка и решение задачи в нулевом приближении. Окончательно постановка задачи для нулевого коэффициента разложения запишется как
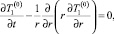 r > 1, t > 0; (11)
r > 1, t > 0; (11)
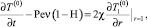
0 < r < 1, t > 0; (12)
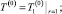
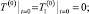
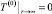 . (13)
. (13)
Заметим, что, усреднив задачу (1)–(4) по r от 0 до 1 интегрально, получим постановку
 r > 1, t > 0;
r > 1, t > 0;
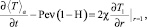
0 < r < 1, t > 0;
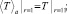
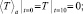
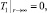
которая совпадает с (11)–(13) с точностью до обозначений. Это определяет физический смысл нулевого коэффициента разложения как некоторым образом осредненное в области 0 < r < 1 поле температуры. В более сложных случаях нелинейных задач и задач с переменными коэффициентами, когда интегральная процедура осреднения не может быть осуществлена, построение нулевого коэффициента представляет асимптотическое осреднение.
Решение задачи для нулевого коэффициента разложения отыскивается с использованием преобразования Лапласа – Карсона [3]. В пространстве изображений задача (11)–(13) примет вид
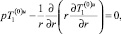 r > 1; (14)
r > 1; (14)
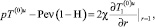 r < 1; (15)
r < 1; (15)
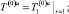
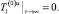 (16)
(16)
Выражение (14) представляет собой известное уравнение Бесселя, решение которого с учетом (16) запишется как 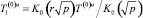 . Подставляя в (15) производную от
. Подставляя в (15) производную от 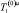 при r = 1, получим для T(0)u алгебраическое уравнение. Таким образом, решения задачи (14)-(16) представятся как
при r = 1, получим для T(0)u алгебраическое уравнение. Таким образом, решения задачи (14)-(16) представятся как
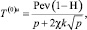 r < 1;
r < 1;
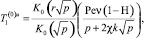 r > 1. (17)
r > 1. (17)
Уточнение физических полей в области осреднения достигается построением первого коэффициента разложения, которое в сложных случаях требует добавочных условий.
Математическая постановка задачи для первого коэффициента разложения. «Расцепленная» математическая постановка для первого коэффициента разложения имеет вид [5]
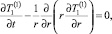 r > 1, t > 0; (18)
r > 1, t > 0; (18)
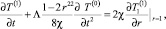
r < 1, t > 0; (19)
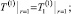
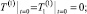
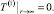 (20)
(20)
В пространстве изображений Лапласа – Карсона задача для первых коэффициентов разложения (18)–(20) запишется как
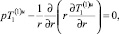 r > 1; (21)
r > 1; (21)
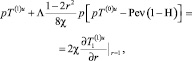
r < 1; (22)
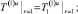
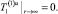 (23)
(23)
Последовательно интегрируя (10), получим общий вид выражения для первого коэффициента разложения
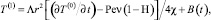
которое в пространстве изображений Лапласа – Карсона примет вид
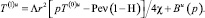
Решение задачи для первого коэффициента разложения отыскивается аналогично решению для нулевого приближения. Выражения для первого коэффициента разложения в скважине и окружающей среде представятся как
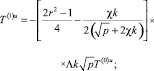 (24)
(24)
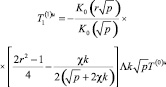 (25)
(25)
соответственно. Выражения для первого коэффициента асимптотического разложения зависят от радиальной координаты во всех областях и позволяют изучать изменение температуры по радиусу трубы. Кроме того, из выражений для первого коэффициента разложения следуют стационарные решения задач, полученные при формальном устремлении времени к бесконечности. В этом смысле построение первого коэффициента разложения представляет важнейшую задачу определения стационарных решений ряда задач теории теплопроводности.
В рассматриваемой задаче (19)–(21) все условия выполняются. В более сложных случаях требуется ослабление начальных и (или) граничных условий. Искомые условия определяются из требования тривиального решения осредненной задачи для остаточного члена, и в этом смысле соответствующие выражения для нулевого и первого приближения названы «в среднем точными».
Задача для остаточного члена. Обозначим сумму слагаемых после первого коэффициента разложения за остаточный член Θ, тогда решение задачи (1)–(4) строится в виде асимптотической формулы
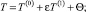
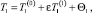 (26)
(26)
где Θ – остаточный член.
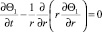 , r > 1, (27)
, r > 1, (27)
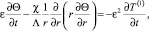 r < 1, (28)
r < 1, (28)
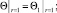
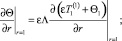 (29)
(29)
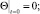
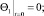
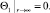 (30)
(30)
Интегрально осредненная в области 0 < r < 1 задача для остаточного члена имеет вид
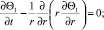 (31)
(31)
 (32)
(32)
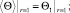
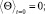

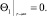 (33)
(33)
Из осреднения выражения, следующего из (6), и условия, следующего из (8), получим
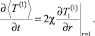
Таким образом, задача (32)–(34) имеет только тривиальное решение. Сумма нулевого и первого коэффициентов разложения представляют собой «в среднем точное» асимптотическое решение для задачи (1)–(4) [5–8].
Точное решение задачи. При решении задачи асимптотическими методами возникает вопрос о близости точного и асимптотического решений. Достоверность развитого метода может быть обоснована сопоставлением полученных асимптотических решений с коэффициентами разложения точного решения параметризованной задачи в ряд Маклорена по формальному параметру. Представленный в данной статье случай допускает точное решение задачи (1)–(4) в пространстве изображений Лапласа – Карсона
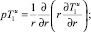 (34)
(34)
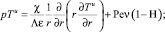 (35)
(35)
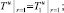
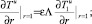
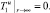 (36)
(36)
Решения задачи (35)–(37) имеют вид
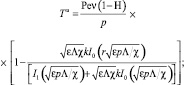 (37)
(37)
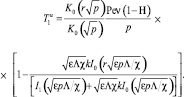 (38)
(38)
Нетрудно убедиться, что Tu при ε → 0 совпадает с выражением (17), а 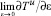 - с выражением (24) для первого коэффициента разложения. Такое сопоставление является прямой проверкой справедливости развитого выше метода решения задач сопряжения.
- с выражением (24) для первого коэффициента разложения. Такое сопоставление является прямой проверкой справедливости развитого выше метода решения задач сопряжения.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор, декан физико-математического факультета, Стерлитамакский филиал, Башкирский государственный университет, г. Стерлитамак;
Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой прикладной информатики и программирования, Стерлитамакский филиал, Башкирский государственный университет, г. Стерлитамак.
Библиографическая ссылка
Филиппов А.И., Ахметова О.В., Зеленова М.А. СОПОСТАВЛЕНИЕ АСИМПТОТИЧЕСКОГО РЕШЕНИЯ ЗАДАЧИ ТЕПЛОПЕРЕНОСА В СКВАЖИНЕ С КОЭФФИЦИЕНТАМИ РАЗЛОЖЕНИЯ ТОЧНОГО РЕШЕНИЯ В РЯД МАКЛОРЕНА // Фундаментальные исследования. 2015. № 2-27. С. 6037-6042;URL: https://fundamental-research.ru/ru/article/view?id=38615 (дата обращения: 14.03.2026).



