Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бутов А.А. 1 Карев М.А. 1 Коваленко А.А. 1 Кононова Г.В. 1

---

1 ФГБОУ ВПО «Ульяновский государственный университет»

В настоящей работе рассматривается модель митотически активных клеток (т.е. не постмитотических, и не клеток с затухающей митотической активностью). Для таких клеток характерно явление полийплоидии. Наряду с многими, как положительными, так и отрицательными эффектами этого явления наблюдается некоторая взаимосвязь его с эффектами активации транспозонов. Эта взаимосвязь проявляется в существовании некоторых компромиссных уровней (как полиплоидии, так и активации транспозонов), которые позволяют достигать значений, оптимальных с точки зрения угроз канцерогенеза, с одной стороны, и мутагенеза активации транспозонов, с другой стороны. С опорой на данные заключения представлен принцип построения математической модели на основе телеграфных процессов в семимартингальных терминах с последующим выводом теоремы, относящейся к классу оптимизационных.

Статья в формате PDF

512 KB

транспозон

полиплоидия

семимартингал

1. Chia N. Dynamics of gene duplication and transposons in microbial genomes following a sudden environmental change / N. Chia, N. Goldenfeld // Physical Review. – 2011. – № 83(2).

2. Gomperc B. On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies // Philosophical Transactions of the Royal Society of London. – 1825. – Vol. 115. – Р. 513–585.

3. Miskey C. DNA transposons in vertebrate functional genomics / C. Miskey Z. Izsvak, K. Kawakami, Z. Ivics // Cellular and Molecular Life Sciences. – 2005. – № 62(6). –P. 629–641.

4. Rasgon J.L. Transposable element insertion location bias and the dynamics of gene drive in mosquito populations / J.L. Rasgon, F. Gould // Insect Molecular Biology. – 2005. – № 14(5). – P. 493–500.

5. Wright S. Transposon dynamics and the breeding system / S. Wright, D. Schoen // Genetica. – 2000. – № 107. – P. 139–148.

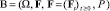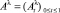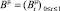Пусть – стохастический базис с обычными условиями Деллашери [1]. Пусть при t ∈ [0, 1] заданы точечные процессы и , определяющие позиции активных транспозонов на хромосомах с нормированными длинами (равными 1). В таких обозначениях наличие активных транспозонов может быть обозначено единичным значением процесса телеграфного типа

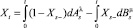(1)

с процессами Aλ и Bμ, имеющими компенсаторы

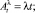
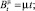
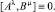(2)

Обозначим xt = EXt. Тогда, очевидно, выполняется соотношение

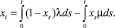(3)

Обозначим среднюю длину транспозона β (β > 0).

Тогда очевидно

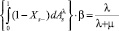, (4)

поскольку, как следует из уравнения (3),

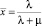(5)

(при стационарном распределении, наблюдаемом в экспериментах x′ = 0, и, следовательно, выполняется (5)).

Из (4) вытекает полезное соотношение для соотношения частоты затухания активности транспозонов и их средней длины

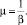(6)

Пусть в клетке существует k ≥ 1 (идентичных) копий хромосомы. Тогда локусы активности транспозонов, разрушающие работу нормальной ДНК, могут быть обозначены 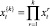со средними значениями на всех k хромосомах, равными

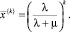(7)

Последнее равенство следует, очевидно, из того, что 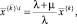поскольку при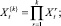

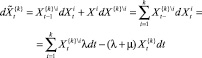
и, следовательно,

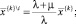
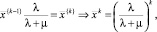(8)

что приводит к нарушениям экспрессии генов за время T > 0, пропорциональное величине

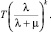(9)

Таким образом, оптимизация работы генома предполагает за некоторое время T минимизацию

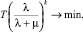(10)

Однако полиплоидия (и это особенно наглядно демонстрирует поведение гепатоцитов) приводит к росту угрозы канцерогенеза, который можно в первом приближении представить в виде вероятности

1 – e–ρTk (11)

с задачей

1 – e–ρTk → min, (12)

где ρ – коэффициент канцерогенной активации генов на любой из k аллельных хромосом при k-полиплоидии.

Таким образом, при формировании полиплоидных структур (наряду с иными задачами и причинами её возникновения) решается задача оптимизации, аддитивно формирующаяся из подзадач (10) и (12):

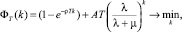(13)

где A > 0 – некоторый, экспериментально (на основе эволюционного обоснования полиплоидии) определяемый коэффициент пропорциональности.

Заметим, что количество активных транспозонов существенно ниже их общего числа. Это приводит к соотношению λ << μ, а также к тому, что δ = –lnβ >> 1, поскольку общая генетическая масса активных транспозонов существенно меньше общего объема хромосомы.

Следовательно, задача (13) редуцируется в приближенную задачу

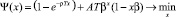, (14)

поскольку Ψ(x) = Φ(x) + ο(x).

Теорема. Решение задачи (14) существует и определяется трансцендентным уравнением

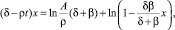
где δ = –lnβ.

Замечание. Решение не только существует, положительно, но и допускает оценку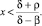

Рецензенты:

Андреев А.С., д.ф.-м.н., профессор, заведующий кафедрой информационной безопасности и теории управления, декан факультета математики и информационных технологий, Ульяновский государственный университет, г. Ульяновск;

Мищенко С.П., д.ф.-м.н., профессор, заведующий кафедрой алгебро-геометрических вычислений, Ульяновский государственный университет, г. Ульяновск.

Библиографическая ссылка