Задача о случайных блужданиях по вершинам графа давно считается классической, в теории случайных процессов это стандартный пример, с которого начинают изучение Марковских процессов. Перемещаясь по дугам из вершины в вершину, движущаяся частица совершает на графе путь (основные определения см. в [1]). Если мы налагаем дополнительные требования на множество допустимых путей (вводим ограничения на достижимость), этот процесс становится немарковским. Общая схема решения задачи о случайных блужданиях на конечных ориентированных графах с ограничениями на достижимость изложена в работе [2]. В настоящей работе мы рассматриваем бесконечный граф-решётку и решаем задачу о случайных блужданиях на графах с ограничениями на достижимость двух типов – смешанная достижимость и магнитная достижимость. Регулярность конструкции графа-решётки и регулярность поставленных ограничений на достижимость позволили нам получить результаты, не пользуясь методом разверток (см. [2]).
Пути на графе-решётке
Рассмотрим один бесконечный ориентированный граф, который будем называть граф-решетка. Множество вершин этого графа Z+×Z+ (здесь Z+ – множество неотрицательных целых чисел). Из каждой вершины (k; l) выходят две дуги, одна в вершину (k + 1; l), другая в вершину (k1; l + ) (рисунок). Будем считать, что все дуги имеют единичную длину.
Ясно, что
1. Граф-решетка не содержит контуров.
2. Все пути на этом графе простые.
3. Из вершины x = (k; l) существует путь в вершину y = (s; t) тогда и только тогда, когда (k ≤ s)&(l ≤ t), при этом длины всех путей равны (s – k) + (t – l). Все эти пути находятся на графе-решетке в прямоугольнике с нижней левой вершиной x и правой верхней вершиной y.
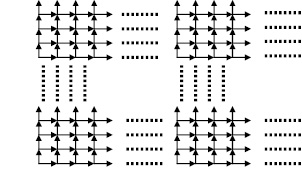
Граф-решётка
Пусть 0 ≤ m ≤ n. Рассмотрим задачу о количестве путей из вершины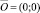 
в вершину 
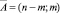. Все пути из 
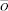в 
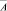имеют длину, равную n и располагаются в соответствующем прямоугольнике. Каждый такой путь будем кодировать n-разрядным двоичным числом, содержащим m единиц и n – m нулей. Единица, стоящая на i-м месте, означает, что на i-м шаге путь проходит по вертикальной дуге, а ноль – означает прохождение по горизонтальной дуге. Таким образом, количество путей, ведущих из вершины 
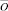в вершину 
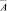, равно количеству n-разрядных двоичных чисел, содержащих m единиц, а оно равно 
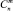. Граф-решетка позволяет сделать наглядным доказательство тождества Паскаля, лежащего в основе построения знаменитого треугольника Паскаля (см. напр. [1]). Действительно, рассмотрим вершины 
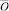и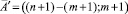 
. Количество путей, ведущих из 
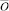в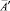 
, равно 
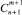, разобьем все множество путей на множество путей, заканчивающихся вертикальной дугой, и множество путей, заканчивающихся горизонтальной дугой. В первом из них содержится 
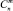путей, а во втором – 
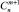путей. По комбинаторному правилу суммы получаем
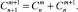
Будем считать, что на дугах заданы вероятности перехода. Вероятность перехода по любой вертикальной дуге будем считать равной p, 0 < p < 1, а по любой горизонтальной дуге равной q, 0 < q < 1, p + q = 1. Тогда вероятность попадания из вершины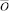 
в вершину 
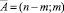по одному из путей равна pm∙qn–m. Вероятность 
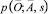попадания из вершины 
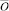в вершину 
за s шагов равна
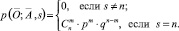
Просуммировав последнее по всем вершинам, находящимся на расстоянии n от вершины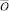 
, получим
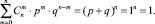
Это соответствует тому, что мы имеем дело с полной группой событий.
Граф-решётка со смешанной достижимостью
Будем теперь рассматривать граф-решётку как граф со смешанной достижимостью (см. [2–4]). Множество дуг U графа со смешанной достижимостью представляет собой объединение непересекающихся непустых множеств UR и UZ, а допустимыми на графе со смешанной достижимостью являются пути, которые не проходят подряд по дугам множества UZ. Будем считать, что на графе-решетке горизонтальные дуги образуют множество UZ, а вертикальные – UR. Допустимыми путями на графе-решётке со смешанной достижимостью являются пути, не содержащие никаких следующих подряд горизонтальных дуг. Другими словами, между любыми двумя соседними горизонтальными дугами пути имеется не менее одной вертикальной дуги. Ясно, что условие существования пути из вершины x = (k; l) в вершину y = (s; t), состоящее в выполнении неравенств (k ≤ s)&(l ≤ t), является теперь только необходимым, но не достаточным.
Пусть 0 ≤ m ≤ n. Рассмотрим задачу о количестве смешанных путей, ведущих из вершины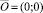 
в вершину 
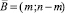. Путь будем кодировать n-разрядным двоичным числом, содержащим m нулей и n – m единиц. Учитывая условие смешанной достижимости, в этих числах между любыми соседними нулями должна содержаться хотя бы одна единица. Обозначим через x1 количество единиц, стоящих перед первым нулями (x1 ∈ Z+), через x2 – количество единиц, стоящих между первым и вторым нулём (x2 ∈ N), через x3 – количество единиц, стоящих между вторым и третьим нулями, (x3 ∈ N), ..., через xm – количество единиц, стоящих между предпоследним и последним нулями (xm ∈ N), через xm+1 – количество единиц, стоящих за последним нулем (xm+1 ∈ Z+). Тогда задача о подсчёте количества таких n-разрядных двоичных чисел равносильна задаче нахождения числа решений уравнения
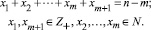(1)
Следуя [1], сделаем в (1) замену переменных
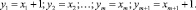
Тогда задача свелась к подсчету числа решений уравнения
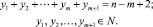(2)
Известно ([1]), что количество решений уравнения (2) равно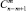 
. Ясно, что должно выполняться неравенство m < n – m + 1. Тогда 
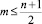. Это неравенство является необходимым и достаточным условием смешанной достижимости на графе-решётке, а именно:
Утверждение 1. Вершина y = (s; t) смешанно достижима из вершины x = (k; l) на графе-решётке тогда и только тогда, когда выполнены следующие условия
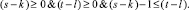(3)
Множество вершин, смешанно достижимых из вершины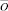 
– это вершины, находящиеся на прямой y = x – 1 и выше этой прямой.
Что будет с процессом случайного блуждания в случае смешанной достижимости, когда запрещено проходить по двум горизонтальным дугам подряд? Как известно ([2, 5]), в этом случае процесс случайного блуждания не является Марковским процессом. Вершины, находящиеся ниже прямой y = x – 1, станут недостижимыми. Пути перестают быть равновероятными.
Рассмотрим случай, когда количество шагов процесса s = 4. В этом случае достижимыми являются только вершины I = (0; 4), II = (1; 3), III = (2; 2). В вершину I ведёт смешанный путь (1111),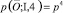 
. В вершину II ведут смешанные пути (1110), (0111), (1011) и (1101) . Вероятность прохождения по первому из них равна p3∙q, по второму и третьему и четвёртому – p2∙q, значит 
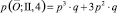. В вершину III ведут смешанные пути (1010), (0101) и (0110). Вероятность прохождения по первому из них равна p∙q2, по второму – q2, по третьему – p∙q2, значит, 
.
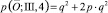Проверим, что сумма вероятностей попадания в эти вершины равна единице. Действительно,
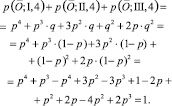
Граф-решётка с магнитной достижимостью
Рассмотрим задачу о случайных блужданиях по графу-решетке с условием неубывающей магнитности [2]. Что это означает? Допустимыми на графе с магнитной достижимостью являются пути, удовлетворяющие следующему условию: если i-му шагу путь прошел через k дуг из множества магнитных дуг и среди дуг, выходящих из конечной вершины i-й дуги, есть магнитные дуги, то i + 1-я дуга должна быть магнитной. Величина k называется уровнем магнитности. Магнитными дугами на графе решётке будем считать вертикальные дуги, а уровень магнитности k = 3.
Рассмотрим задачу о вероятности попадания из вершины (0;0) в вершины решетки за пять шагов по магнитным путям.
Количество магнитных путей, ведущих в вершину (5;0), равно 1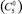 
, а вероятность прохождения по этому пути равна q5, 
.
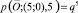Количество магнитных путей, ведущих в вершину (4;1), равно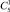 
, а вероятность прохождения по каждому из них равна p∙q4, т.е. 
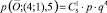. Количество магнитных путей, ведущих в вершину (3; 2), равно 
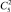, а вероятность прохождения по каждому из них равна p3∙q3, 
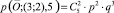Количество магнитных путей, ведущих в вершину (2; 3), равно 
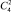, а вероятность прохождения по каждому из них равна p3∙q2, 
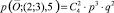. Количество магнитных путей, ведущих в вершину (1;4), равно 
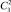, а вероятность прохождения по каждому из них равна p3∙q, 
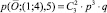. Количество магнитных путей, ведущих в вершину (0; 5), равно 
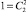, а вероятность прохождения по этому пути равна p3, 
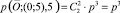. Вероятности попадания из вершины (0;0) за n шагов при уровне магнитности k = 3 в точки, находящиеся на расстоянии равном n: (n; 0), (n – 1; 1), (n – 2; 2), (n – 3; 3), (n – 4; 4), ..., (2; n – 2), (1; n – 1), (0; n).
таковы:
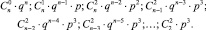
Учитывая, что полная вероятность попасть из вершины (0;0) в какую-нибудь из этих вершин равна 1, мы получаем тождество
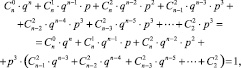(4)
если p + q = 1.
В случае отсутствия магнитности (k = 0) это тождество превращается в формулу бинома Ньютона.
Для уровня магнитности 0 < k < n получаем тождество:
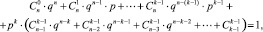(5)
если p + q = 1.
Пусть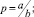 
a, b ∈ Z+ (0 < a < b); 
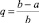, тогда из (5) получаем
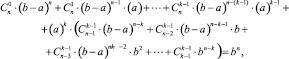
1 ≤ k ≤ n. (6)
Приведём пример «работы» тождества (6). Пусть a = 3; b = 5; b – a = 2; n = 5; k = 2..
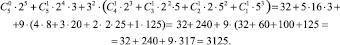
Заключение
Мы рассматривали задачу о случайных блужданиях по графу-решётке из вершины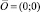 
. Случай произвольной «стартовой» точки получается из рассмотренного с помощью соответствующего параллельного переноса начала координат в «стартовую» точку. Случай 
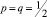рассмотрен нами в [6].
Комбинаторное тождество (6) (о комбинаторных тождествах [7, 8]) можно считать обобщением формулы бинома Ньютона.
Рецензенты:
Белявский Г.И., д.т.н., профессор, заведующий кафедрой высшей математики и исследования операций, Южный федеральный университет, г. Ростов-на-Дону;
Наседкин А.В., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования, Южный федеральный университет, г. Ростов-на-Дону.
Библиографическая ссылка
Ерусалимский Я.М. СЛУЧАЙНЫЕ БЛУЖДАНИЯ ПО ГРАФУ-РЕШЁТКЕ. НЕМАРКОВСКИЙ СЛУЧАЙ // Фундаментальные исследования. 2015. № 2-27. С. 6013-6017;URL: https://fundamental-research.ru/ru/article/view?id=38610 (дата обращения: 02.04.2025).