Современные летательные аппараты (ЛА) оснащены системами управления, которые реализуют различные траектории полета с учетом влияния внешней среды, возможного противодействия противника, а также изменения состояния самого ЛА. Решение задач управления ЛА во многом определяется уровнем точности измерительных систем. При управлении ЛА источником информационно-измерительных сигналов являются различные системы ориентации и навигации, в частности инерциальные навигационные системы (ИНС).
Современные ИНС имеют погрешности, обусловленные различными факторами. Эти погрешности можно компенсировать посредством конструкторских и алгоритмических методов. Реализация конструкторских методов требует значительного времени и новой технологической базы, а алгоритмические методы легко реализуются и позволяют повысить точность серийных измерительных систем. Алгоритмические методы повышения точности ИНС, как правило, включают алгоритмы оценивания, управления, прогноза и комплексирования [6]. При функционировании ИНС ЛА на атмосферном участке на длительных интервалах времени без коррекции от внешних измерительных систем наземных станций ближней и дальней навигации, спутниковых систем для компенсации погрешностей автономной ИНС используют способы формирования корректирующего сигнала на основе информации с датчиков углов прецессии гироскопов [2], формируют компенсационные сигналы с помощью алгоритмов фильтрации [1, 6].
Существенно повысить точность ИНС ЛА можно с помощью использования сигналов от внешнего по отношению к ИНС источника информации. В настоящее время наиболее точными являются навигационные системы с коррекцией от спутников. Рассматриваются различные схемы коррекции навигационных систем и алгоритмические методы повышения точности навигационной информации при функционировании систем в условиях активных и пассивных помех, а также при сложном движении несущего объекта.
Предлагается в качестве алгоритма оценивания рассмотреть фильтр Калмана, нелинейный фильтр Калмана, модифицированный фильтр Калмана с использованием генетического алгоритма.
Проверка работоспособности и эффективности алгоритмов осуществляется с помощью моделирования по данным лабораторного эксперимента. Проверка работоспособности алгоритмов проведена с использованием данных лабораторного эксперимента с реальной инерциальной навигационной системой КИНД34-059.
Коррекция навигационных систем с использованием сигналов GPS
Наиболее точная коррекция современных ИНС осуществляется алгоритмическим путем с использованием информации от GPS (рис. 1). В качестве алгоритмов коррекции часто используются различные алгоритмы оценивания для вычисления погрешностей измерительных систем [1, 2, 6]. В качестве алгоритма оценивания часто используют фильтр Калмана и его модификации [1, 6]. В настоящее время развиваются два основных направления исследований: углубленное изучение и анализ теории Байеса [1]; применение современных эволюционных алгоритмов, а именно подхода самоорганизации [3, 5], генетических алгоритмов (ГА) [10, 11] и их комбинаций для модификации традиционных фильтров Калмана.
Рис. 1. Схема коррекции ИНС с использованием GPS: ИНС –
инерциальная навигационная система; GPS – система глобального
позиционирования; О – алгоритм оценивания; θ – истинная навигационная
информация; z – измерение; x – состояние системы; 
– оценки; 
– ошибки оценивания
Алгоритмы оценивания
Фильтр Калмана обеспечивает рекурсивное решение для линейной задачи оптимального оценивания в стационарных, а также нестационарных условиях.
В практических приложениях априорная информация о статистических характеристиках входного и измерительного шумов достоверно неизвестна, что может приводить к расходящемуся процессу оценивания [1, 6]. Поэтому для коррекции ИНС от GPS используют адаптивные алгоритмы оценивания [6], являющиеся модификациями фильтра Калмана.
При совершении ЛА маневров углы отклонения гиростабилизированной платформы (ГСП) ИНС относительно выбранной системы координат нарастают, и линейная модель ее погрешностей, полученная с учетом предположения о горизонтальном движении несущего объекта и малости углов стабилизации, становится неадекватной реальному процессу [6].
К точности решения поставленных задач на современных ЛА предъявляются жесткие требования. Поэтому в практических приложениях используется комплексирование ИНС с GPS и последующая обработка навигационной информации посредством нелинейного фильтра Калмана.
Пусть уравнение для вектора состояния имеет вид
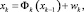(1)
где xk – вектор состояния; Φk(xk–1) – нелинейная матрица модели, и часть вектора состояния измеряется:
zk = Hkxk + υk, (2)
где zk – вектор измерений; Hk – матрица измерений; wk и υk – дискретные аналоги гауссовского белого шума с нулевыми математическими ожиданиями и матрицами ковариаций Qk и Rk соответственно, некоррелированные между собой, уравнения фильтра Калмана примут вид [9]
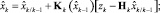
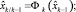
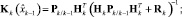(3)
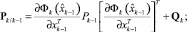
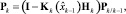
где I – единичная матрица; Pk – ковариационная матрица ошибок оценивания.
Но такой подход применим лишь в случае унимодального характера апостериорной плотности, когда апостериорная плотность многоэкстремальна, используется алгоритм, в котором апостериорная плотность представлена набором дельта-функций.
Недостатком представления апостериорной плотности в виде дельта-функций является то, что не учитывается локальное поведение функции Φk в окрестности узлов сетки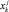 
. Ясно, что увеличение количества узлов сетки позволит повысить точность, но при этом возрастет объем вычислений.
Известен алгоритм, позволяющий учесть локальное поведение функций Φk(xk–1), построен на полигауссовской аппроксимации апостериорной плотности [9].
Перечисленные варианты реализаций нелинейного фильтра Калмана предполагают линеаризацию модели погрешностей ИНС с помощью ряда Тейлора, представление апостериорной плотности в виде набора d-функций или замену апостериорной плотности системой частных гауссовских плотностей, взятых с различными весами. В итоге в фильтре Калмана используются только линейные модели погрешностей ИНС.
Использование нелинейных моделей в фильтре Калмана в общем случае затруднительно ввиду того, что апостериорная плотность вектора состояния в этом случае не является гауссовской, и, следовательно, получить легко алгоритмизируемые рекуррентные соотношения для вычисления оценок вектора состояния не представляется возможным.
Известны подходы [1, 9], в рамках которых реализация фильтра Калмана сведена к решению стохастического дифференциального уравнения в частных производных, записанного в форме Ито или в форме Стратоновича. Однако практическая реализация решения этого уравнения сложна еще и потому, что при интегрировании этих уравнений необходимо применять специальные правила, не совпадающие с обычными правилами математического анализа.
Другим недостатком упомянутых вариантов реализации нелинейного фильтра Калмана является невысокая точность исходной нелинейной модели. Эта модель получена посредством анализа физических законов, которые лежат в основе функционирования исследуемой конструкции ИНС. Однако учитываются лишь некоторые основные законы, принципы и возмущающие факторы, определяющие погрешности ИНС. Поэтому при маневрировании ЛА возникает необходимость идентификации параметров модели погрешностей ИНС. Для решения задачи совместного оценивания параметров и состояния объекта могут быть использованы метод инвариантного погружения с расширенным вектором состояния и расширенный фильтр Калмана. Однако расширение вектора состояния путем включения в него неизвестных параметров приводит к тому, что уравнения модели становятся нелинейными даже в случае линейной по состоянию и по параметрам исходной модели.
При реализации расширенного фильтра Калмана оценки, как правило, имеют расходящийся характер, обусловленный отсутствием априорной информации о статистических характеристиках шумов и из-за погрешностей линеаризации.
Решение нелинейной задачи совместного оценивания параметров и состояния может быть получено посредством адаптивных наблюдателей [6, 7]. Преимуществом адаптивных наблюдателей является отсутствие необходимости проведения операции линеаризации, что исключает весьма существенные ошибки, связанные с линеаризацией уравнений, описывающих оцениваемый процесс. Использование адаптивных наблюдателей возможно лишь в специфических случаях. Например, динамика вектора состояния описывается линейными уравнениями, а измерения нелинейно зависят от компонент вектора состояния объекта, нелинейный по состоянию объект, линейно зависящий от параметров и др.
На погрешность ИНС оказывают влияние многообразные возмущающие факторы, многие из которых коррелированы и, как правило, описываются с помощью вероятностных характеристик или стохастических уравнений. Однако достоверная информация о статистических характеристиках на практике отсутствует. Поэтому при оценивании погрешностей ИНС с использованием сложных моделей необходимо осуществлять идентификацию параметров и структуры модели в процессе функционирования системы. В некоторых случаях можно использовать подходы, базирующиеся на теории дифференциальной геометрии [4], которые позволяют проводить линеаризацию без потери точности.
В качестве алгоритма идентификации может быть использован, например, фильтр Вольтерра второго порядка [8]. В качестве основной трудности реализации подобных алгоритмов является необходимость обработки большой базы данных, характеризующей работу идентифицируемой системы. Конструктивным подходом в решении данной задачи является использование фильтрующей структуры в виде последовательности Вольтерра. Однако одной из главных причин достаточно редкого применения методики фильтрации Вольтерра на практике является значительная сложность, связанная с реализацией фильтров Вольтерра. Количество операций при реализации увеличивается экспоненциально с увеличением порядка фильтра. Упрощение реализации фильтра Вольтерра возможно осуществить путем параллельной комбинации линейного и квадратичного фильтров [8].
Наиболее полно учесть все особенности характера изменения погрешностей ИНС и, что особенно важно, конкретной ИНС в условиях каждого конкретного полета возможно посредством построения нелинейной модели с помощью одного из эволюционных алгоритмов – алгоритма самоорганизации и генетического алгоритма [5, 10].
Нелинейная модель используется в качестве эталонной модели для обеспечения адекватности модели фильтра Калмана и реального процесса изменения погрешностей ИНС. На рис. 2 представлена схема коррекции ИНС с использованием генетического алгоритма (ГА).
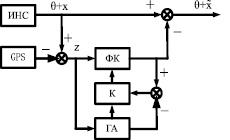
Рис. 2. Схема коррекции ИНС с использованием генетического алгоритма: ИНС – инерциальная навигационная система; GPS – система глобального позиционирования; ФК – фильтр Калмана; ГА – генетический алгоритм; К – критерий – индикатор расходимости процесса оценивания; θ – истинная навигационная информация; x – истинные ИНС ошибки; 
– оценки ИНС ошибок
Рис. 3. Навигационная система КИНДЗ4-059
Моделирование по данным лабораторного эксперимента
Для того чтобы определить эффективность алгоритмов оценивания, использованы данные полунатурного эксперимента с реальной навигационной системой КИНД34-059 (рис. 3).
Для оценивания ошибок ИНС использованы: линейный фильтр Калмана (ЛФК), нелинейный фильтр Калмана (НФК) и модифицированный нелинейный фильтр Калмана с использованием генетического алгоритма (НФК с ГА).
Ошибки ИНС в определении местоположения вычислены в течение периода времени 0–5 ч показаны в таблице.
Ошибки ИНС в определении местоположения
|
ИНС с алгоритмом |
Ошибки, восточная составляющая, м |
Ошибки, северная составляющая, м |
|
ЛФК |
77 |
83 |
|
НФК |
44 |
28 |
|
НФК с ГА |
2,8 |
1,3 |
В соответствии с результатами лабораторных экспериментов модифицированный фильтр Калмана с генетическим алгоритмом в условиях маневрирования ЛА превосходит по точности классический нелинейный фильтр Калмана и линейный фильтр Калмана, работает с высокой точностью, и его рекомендовано использовать для построения моделей погрешностей ИНС.
Выводы
Исследованы способы обработки навигационной информации ЛА в схеме коррекции ИНС в выходном сигнале. Представлены линейный и нелинейный фильтры Калмана. Анализ особенностей различных способов реализации фильтра Калмана показал необходимость использования апостериорной информации о модели исследуемого процесса.
В качестве алгоритма обработки информации предложено использовать нелинейный фильтр Калмана, модифицированный с помощью генетического алгоритма.
Эффективность предложенного алгоритма проверена с помощью математического моделирования и моделирования по данным полунатурного эксперимента с системой КИНД34-059. Результаты моделирования продемонстрировали высокую точность модифицированного нелинейного фильтра Калмана с использованием генетического алгоритма.
Рецензенты:
Пролетарский А.В., д.т.н., профессор, декан факультета «Информатика и системы управления», зав. кафедрой «Компьютерные системы и сети», МГТУ им. Н.Э. Баумана, г. Москва;
Галиновский А.Л., д.т.н., профессор кафедры «Технологии ракетно-космического машиностроения», МГТУ им. Н.Э. Баумана, г. Москва.
Библиографическая ссылка
Цибизова Т.Ю., Шэнь Кай, Неусыпин К.А. ИССЛЕДОВАНИЕ АЛГОРИТМОВ ОЦЕНИВАНИЯ В ЗАДАЧЕ КОРРЕКЦИИ НАВИГАЦИОННЫХ СИСТЕМ ЛЕТАТЕЛЬНЫХ АППАРАТОВ // Фундаментальные исследования. – 2015. – № 6-2. – С. 301-305;URL: https://fundamental-research.ru/ru/article/view?id=38560 (дата обращения: 23.11.2024).