Для построения геолого-геофизических моделей осадочных бассейнов и их фрагментов эффективно применение ведущих современных технологий интерпретации гравиметрических данных. Для крупных плотностных структур типа осадочных бассейнов необходимо проводить постановку и решение интерпретационных задач с учётом условий слабой изученности и сложного строения среды. Это позволяет сделать технология, основанная на критериальном подходе к решению обратных задач гравиразведки [1–5, 7]. Она основана на комплексном анализе всей имеющейся геолого-геофизической информации. Возникает проблема выбора модели среды, которая должна быть положена в основу изучения имеющихся в осадочных бассейнах образований.
При решении задач реконструкции геологической среды построенная модель распределения физического параметра должна соответствовать с заданной степенью приближения наблюдаемым физическим полям. Три взаимоувязанных элемента, составляющих содержание понятия модели задачи: модель среды, модель поля и модель физического явления. Выделяются прямая и обратная задачи геофизики. Во введённых терминах прямая задача состоит в нахождении модели поля по известным моделям среды и физического явления. Обратная задача заключается в реконструкции модели среды по модели поля и явления. Исходную информацию, имеющуюся для изучения геологической среды, можно представить в виде совокупности трёх компонент [2, 5, 6, 8]: одномерные объекты, например данные скважин; двухмерные объекты, т.е. некие профильные наблюдения, и трёхмерные наблюдения, в частности наблюдаемые геофизические поля.
Наиболее общей и полной в смысле количества априорной информации моделью среды является модель распределения плотности, или плотностная модель. Она может быть использована для решения задач локального прогнозирования, т.е. оценки локальных изменений физических свойств, в пределах отдельных блоков, пластов и разреза в целом. Эта модель является математической основой схем интерпретации на классе непрерывных функций или прогнозирования непрерывного геолого-геофизического разреза. Структурная геолого-геофизическая модель является упрощённым вариантом. Введение данной модели необходимо для решения задач, где априори вводится предположение о слоистом строении среды. В рамки таких предположений укладываются как классические структурные задачи – изучение поверхности кристаллического фундамента, структур синклинального и антисинклинального типов, надвиговых структур, так и задачи солянокупольной тектоники.
Для описания моделей среды используются различные варианты задания данных и соответствующие им постановки прямых задач гравиразведки для двухмерного и трёхмерного случая. Суть двухмерной постановки состоит в следующем [2, 5, 6]. Часто при интерпретации гравиразведочных данных аномалии гравитационного поля носят ярко выраженный линейный характер. Тогда естественно ввести предположение о том, что источник поля имеет бесконечную протяжённость по какому-то направлению, а в каждой вертикальной плоскости, перпендикулярной к этому направлению, сечение носителя и распределение масс по этому сечению одни и те же. Такие тела принято называть двухмерными, а соответствующие им поля – двухмерными или плоскими.
Плотностная двухмерная модель (модель распределения плотности). Задание исходной информации производится по профилю. Используем прямоугольную систему координат с осью Oz, направленной вниз к массам, и осью Ox, совмещённой с дневной поверхностью и направленной вдоль линии задания данных. Модель среды конструируется в области S, лежащей в нижнем полупространстве. Для каждой точки (x, z) ставим в соответствие значения параметра плотности σ = σ(x, z).
Структурная двухмерная модель. Для представления структурной модели каждой точке x сопоставляется глубина залегания z = fk(x) соответствующей границы k = 0, 1, ..., N, лежащей в области S, ограниченной горизонтальной полосой П. Каждый из пластов характеризуется своим неизменным по вертикали параметром плотности σk(x).
Аппроксимационные двухмерные модели, являясь тоже разновидностью плотностных, представляют собой разбиение области S сеткой на ячейки Sj с плотностью σj так, что 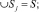
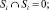 j = 1, ..., J конфигурация которых подбирается таким образом, чтобы изучаемый объект можно было ими хорошо приблизить.
j = 1, ..., J конфигурация которых подбирается таким образом, чтобы изучаемый объект можно было ими хорошо приблизить.
Исходные данные в условиях недоопределенности задаются системой профилей Γ, Γ = {Γl}, l = 1, ..., P, l – геолого-геофизические разрезы. Систему координат рассматриваем с осью Oz, направленной вниз и плоскостью xOy – совмещённой с дневной поверхностью. Модель среды конструируется в области V, лежащей в нижнем полупространстве. Для всех разрезов имеются координаты начала и конца в общей системе координат.
Плотностная объёмная модель. Для представления модели данного вида каждой точке v = (x, y, z) пространства V сопоставляется значение параметра плотности σ = σ(v).
Структурная объёмная модель. Каждой точке s = {x, y} пространства V, ограниченного полосой П, сопоставляется глубина залегания z = fk(s) границы k = 0, 1, ..., N. Каждый из пластов характеризуется своим параметром плотности σk(s), неизменным по вертикали в пределах каждого из пластов. Среди структурных моделей можно выделить:
1) модели, где плотность σk(s) = σk постоянна в пределах каждого из N + 1 пластов;
2) модели, где плотность σk,q(s) может меняться не только в пределах k-го пласта, но и в пределах q блоков, находящихся в составе данного пласта.
Модель первого вида является идеализированной, поэтому наибольший интерес представляет модель, где σk(s) ≠ σk, т.е. плотность пласта не является постоянной. В этом случае модель представляет собой следующее:
● границы, ограничивающие пласты, представляют собой однозначные функции пространственных координат zk = fk(s), k = 0, 1, ..., N + 1;
● плотность пласта, заключённого между k-й и k + 1-й границами, есть функция горизонтальных координат σk+1 = σk+1(s), k = 0, 1, ..., N;
● нулевая граница есть горизонтальная пластина с глубиной f0 и плотностью пласта σ0;
● плотность среды ниже границы с номером N есть σN+1;
● величины f0, σN+1, σ0 считаются постоянными;
● объёмная модель 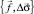 имеет в качестве своего следа на поверхности {l} – проходящей через линию Гl нормально к дневной поверхности двухмерную модель
имеет в качестве своего следа на поверхности {l} – проходящей через линию Гl нормально к дневной поверхности двухмерную модель 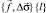 .
.
Для объёмной структурной модели введём краткое обозначение:
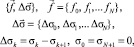
где Δσk – контрастность k-го пласта.
Аппроксимационные объемные модели представляют собой разбиение области V сеткой на подобласти Vj с плотностью σj так, что 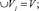
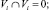 j = 1, ..., J.
j = 1, ..., J.
Классические аппроксимационные модели характеризуются призматическим видом подобластей. Модели этого вида могут иметь в качестве аппроксимирующих тел также и другие тела: шар, пирамиду и др. Такие конструкции ориентированы на задачи типа рудных.
Иерархическая схема объёмных моделей среды, используемых гравиразведкой и в дальнейшем обозначаемых x(v), приведена на рис. 1.
В зависимости от вида модели среды модель явления, которая суть оператор прямой задачи A, может описывать плотностные и структурные задачи гравиразведки.
Ax = U. (1)
Моделью поля в этих задачах можно считать значения вертикальной составляющей гравитационного потенциала в конечном числе точек. В случае двухмерных задач это будет двухмерный массив (x0, uz), в случае трёхмерной – трёхмерный (x0, y0, uz). Под решением обратной задачи [1, 2, 8] понимают нахождение распределения источников x (плотность σ(v) либо конфигурация границ f(s)) при введённых о них модельных представлениях по заданным наблюдаемому полю U и оператору прямой задачи A(x).
Оператор прямой двухмерной плотностной задачи гравиразведки. Вертикальная производная гравитационного потенциала uz(x0, z0), где точка (x0) регистрируется на поверхности в E+(z > 0) с уравнением z0 = ψ(x0), задана следующим соотношением между uz(x0, z0) и σ = σ(x, z):
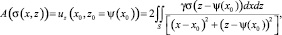 (2)
(2)
где g = 6,673⋅10–5 (поле в миллигалах, расстояния в метрах, плотность в г/см3) – гравитационная постоянная.
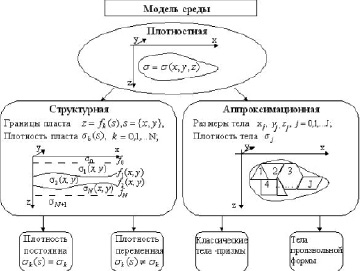
Рис. 1. Иерархическая схема объёмных моделей среды
Оператор прямой двухмерной структурной задачи гравиразведки. Для структурной модели среды, где система границ 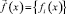 имеет плотности
имеет плотности 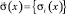 , связь с вертикальной производной гравитационного поля uz(x0, z0) определена соотношением
, связь с вертикальной производной гравитационного поля uz(x0, z0) определена соотношением
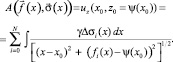 (3)
(3)
Оператор прямой трёхмерной плотностной задачи гравиразведки. Вертикальная производная гравитационного потенциала uz(v0), где v0 = (x0, y0, z0) и точка (x0, y0) = s0 ∈ E0 регистрируется на поверхности с уравнением z0 = ψ(s0), задана следующим соотношением между uz(v0) и σ = σ(v):
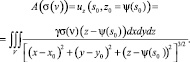 (4)
(4)
Оператор прямой трёхмерной структурной задачи гравиразведки. Для структурной модели среды для простоты плотность каждого пласта примем постоянной. Вертикальная производная гравитационного потенциала Uz(v0), в точке A(v0), вычисляется по формуле:
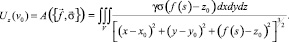 (5а)
(5а)
Формула (5а) для объёмной структурной модели среды в случае, когда z0 = ψ(s0):
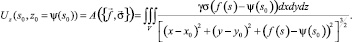 (5b)
(5b)
Вычислив в (5b) интеграл по переменной z и представив результат в виде суммы по N + 1 границе, получаем
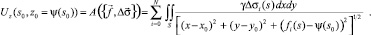 (5c)
(5c)

Рис. 2. Оператор объёмной прямой задачи гравиразведки для разных видов моделей среды
Оператор прямой трёхмерной задачи гравиразведки для аппроксимационной модели. Для каждого элемента Vj задаётся значение плотности 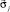 , а гравитационное поле рассчитывается по формуле
, а гравитационное поле рассчитывается по формуле
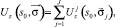
где
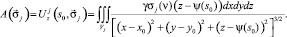 (6)
(6)
Виды модели явления для прямой задачи гравиразведки можно представить в виде схемы (рис. 2).
Наиболее полной и общей моделью среды, используемой гравиразведкой и позволяющей описывать любые неоднородности, является модель функции плотности как функции пространственных координат, однако она обладает серьёзными недостатками. Объясняется это тем, что по гравиметрическим данным не может быть восстановлено распределение плотности в нижнем полупространстве. Поэтому для изучения строения осадочных бассейнов следует использовать модели структурного типа.
Рецензенты:
Бурмистрова О.Н., д.т.н., заведующая кафедрой технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Андронов И.Н., д.т.н., заведующий кафедрой сопротивления материалов и деталей машин, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Библиографическая ссылка
Кобрунов А.И., Мотрюк Е.Н., Ломинский Д.О. ПОСТРОЕНИЕ МОДЕЛЕЙ СЛОЖНОПОСТРОЕННЫХ ГЕОЛОГИЧЕСКИХ СРЕД ПО ГРАВИМЕТРИЧЕСКИМ ДАННЫМ // Фундаментальные исследования. 2015. № 6-2. С. 246-250;URL: https://fundamental-research.ru/ru/article/view?id=38549 (дата обращения: 26.02.2026).



