Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Орлова И.В. 1 Турундаевский В.Б. 2

---

1 Финансовый университет при Правительстве Российской Федерации

2 Московский государственный университет экономики

В статье делается выбор между двумя наиболее применяемыми на практике методами оценки матрицы нагрузок: методом главных осей и методом максимального правдоподобия Лоули. В силу ряда причин рекомендуется использовать метод максимального правдоподобия. Однако методом нельзя пользоваться, если дисперсии некоторых специфических факторов равны нулю. Предлагается метод решения задачи в этом случае. Смысл метода состоит в добавлении к исходным переменным искусственно сгенерированных специ­фических факторов, с тем, чтобы к преобразованным данным можно было применить метод максимального правдоподобия. Предлагаемый метод пригоден к использованию и в случае коллинеарности исходных признаков, что расширяет возможности применения факторного анализа. Статья содержит 6 подразделов: 1. Введение. 2. Выбор метода оценки матрицы нагрузок на общие факторы. 3. Получение оценок матриц L и V. 4. Оценка числа общих факторов. 5. Случай вырожденного распределения.

Статья в формате PDF

743 KB

наблюдаемые признаки

ковариационная матрица

корреляционная матрица

выборочная ковариационная матрица

факторный анализ

общие факторы

специфические факторы

матрица нагрузок на факторы

вырожденное распределение

метод максимального правдоподобия

распределение Уишарта

Дубров А.М., Турундаевский В.Б., Френкель А.А. О задачах факторного анализа при отсутствии части специфических факторов // Учёные записки по статистике. т. 33. Прикладной многомерный статистический анализ. – М.: Наука, 1978.

Окунь Я. Факторный анализ: пер. с польск. – М.: Статистика, 1974.

Харман Г. Современный факторный анализ. – М.: Статистика, 1972.

Lawley D.N., Maxwell A.E. Factor Analysis as a Statistical Method, 2nd ed. – London: Butterworths, 1971.

Lawley D.N. Some new results in maximum likelihood factor analysis. Proceeding of Royal Society of Edinburgh, 1966–1967, v. A67.

1. Пусть x₁, x₂, …, x_p – p наблюдаемых признаков, 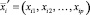– результаты i-го наблюдения признаков, i = 1, 2, …, n, Х = (x_ij) – матрица наблюдений (исходных данных). В факторном анализе предполагается, что x_j является линейной комбинацией m линейно независимых факторов, так называемых «общих факторов» f₁, f₂, …, f_m, плюс «специфический» для данного признака фактор e_i, некоррелированный ни с общими факторами, ни с другими специфическими факторами,

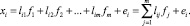(1)

Будем считать x_i центрированными, а факторы – ортогональными:

M(x_i) = 0; M(f_j) = 0;

M(e_i) = 0; σ²(f_j) = 1;

σ²(e_i) = v_i; cov(f_i, f_j) = 0.

Общие факторы f_j являются «причиной» корреляций между признаками x_i. Эти факторы представляют собой непосредственно не измеряемые, скрытые (латентные) переменные, в той или иной мере связанные с исходными наблюдаемыми переменными. Ковариационная матрица ∑ исходных признаков x_i, в соответствии с моделью факторного анализа (1), может быть представлена в виде

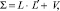(2)

где L = (l_ij) – матрица нагрузок на общие факторы, i = 1, 2, …, p, j = 1, 2, …, m; V – диагональная матрица дисперсий специфических факторов e_i. Диагональные элементы матрицы 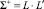представляют собой дисперсии признаков, объясняемые m общими факторами. Эти элементы называются общностями, а сама матрица ∑⁺ – редуцированной корреляционной матрицей.

Выбор метода оценки матрицы нагрузок на общие факторы

Оценки матрицы нагрузок L обычно получают одним из двух способов: методом главных осей или методом максимального правдоподобия [1, 2, 4]. В методе главных осей в качестве оценок матрицы нагрузок выбирают первые m собственных векторов редуцированной корреляционной матрицы ∑⁺, соответствующие наибольшим собственным значениям матрицы ∑⁺. В методе максимального правдоподобия оценка матрицы нагрузок получается путём максимизации функции правдоподобия, считая, что вектор наблюдаемых признаков имеет многомерное нормальное распределение. Хотя оба метода направлены на максимальное приближение внедиагональных элементов корреляционной матрицы, тем не менее методы дают несколько различные результаты. При этом, как показали результаты численного моделирования, метод максимального правдоподобия приближает корреляционную матрицу немного лучше метода главных осей, даже если вектор наблюдаемых переменных 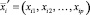не имеет многомерное нормальное распределение. При этом метод максимального правдоподобия имеет под собой строгое математическое обоснование и оценки максимального правдоподобия обладают рядом хороших свойств, как-то: состоятельность, асимптотическая эффективность и асимптотическая несмещённость. Поэтому выбор метода максимального правдоподобия является предпочтительным. Однако метод максимального правдоподобия для оценки матрицы нагрузок не может применяться в некоторых ситуациях, например когда дисперсии специфических факторов равны нулю. В этой ситуации нами предлагается добавить в процесс оценивания преобразование исходных данных, с тем чтобы к преобразованным данным можно было применить метод максимального правдоподобия. Рассмотрим подробнее метод решения задач факторного анализа в этих ситуациях.

При практическом использовании факторного анализа часто возникают следующие ситуации:

1) некоторые специфические факторы отсутствуют в факторной модели;

2) выборочная ковариационная матрица исходных переменных не является положительно определенной.

Пусть 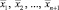– выборка из р-мерной нормальной совокупности N (0, ∑).

Допустим, что вектор генеральной совокупности удовлетворяет модели факторного анализа (1)

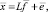(3)

где 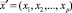– вектор наблюдаемых переменных,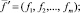 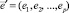– векторы общих и специфических факторов соответственно, не наблюдаемые непосредственно; L = (l_jk) – матрица нагрузок на общие факторы.

В модели (3) предполагается, что (m + p)-мерный вектор факторов 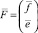имеет нулевое математическое ожидание и ковариационная матрица 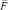имеет вид

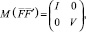
где 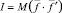– единичная матрица; 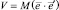– диагональная матрица.

Из модели (3) вытекает, что ковариационная матрица вектора равна

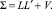(4)

В приложениях факторного анализа возникают следующие задачи [1]:

1. Получение оценок матриц L и V.

2. Оценка числа общих факторов m.

3. Решение первых двух задач в условиях сильной коррелированности переменных, когда некоторые из них являются линейными комбинациями остальных.

Обозначим через S выборочную ковариационную матрицу вектора .

Допустим, что ковариационная матрица ∑ не вырождена. Тогда матрица S имеет распределение Уишарта, и оценка максимального правдоподобия матриц L и V получается из условия максимизации функции Z₀ [4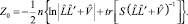, 5]:

(5)

В литературе описаны два основных подхода к решению задачи максимизации функции Z₀ [2, 3, 4]. В обоих известных методах, основанных на них, предполагается, что все оценки дисперсий специфических факторов 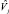отличны от нуля. Однако в практических исследованиях встречаются такие матрицы S, для которых некоторые оценки 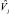близки к нулю. Это может явиться следствием одной из следующих причин:

a) в модели (3) некоторые дисперсии специфических факторов vj равны нулю, т.е. размерность вектора факторов 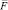меньше m + р. В данной ситуации при любом объеме выборки некоторые оценки 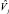могут быть близки к нулю;

б) в модели (3) некоторые v_j близки к нулю; в этом случае, если объем выборки был бы достаточно велик, все оценки дисперсий 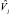были бы больше нуля.

В практических расчетах матрица S иногда не является положительно определенной. Это может быть вызвано тем, что

а) в модели факторного анализа (3) больше, чем m, специфических факторов имеют нулевую дисперсию ( имеет вырожденное распределение);

б) определитель |∑| близок к нулю, и вследствие недостаточно большого объема выборки или ошибок округления матрица S может оказаться не положительно определённой.

Если S не является положительно определенной, то плотность распределения Уишарта равна нулю и мы не можем воспользоваться для оценки матриц нагрузок L и V функцией максимального правдоподобия [4].

Поскольку проверка гипотез о числе общих факторов производится после того, как определены оценк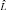и и 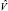[4], то в рассматриваемых ситуациях мы не сможем проверить эти гипотезы. Если максимум функции правдоподобия (5) ищется методом Лоули [4], то число общих факторов m и начальные приближения оценок 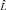и 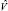часто находят центроидным методом. Следует отметить, что в рассматриваемых ситуациях мы не сможем оценить число общих факторов также и в центроидном методе.

Итак, в ряде случаев нельзя использовать разработанный аппарат оценок максимального правдоподобия матриц 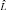и и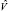, соответственно, проверить гипотезы о числе общих факторов.

Для решения этих задач можно предложить искусственно увеличивать дисперсии специфических факторов.

Получение оценок матриц L и V

Пусть 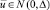– случайная величина с диагональной ковариационной матрицей, не зависящая от . Обозначим через выборочную ковариационную матрицу случайного вектора и через – матрицу выборочных коэффициентов ковариации векторов и ,

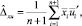
где , 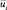– векторы значений и в i-м наблюдении, n + 1 – объем выборки.

Для того, чтобы дисперсии всех специфических факторов сделать отличными от нуля, прибавим к обеим частям модели (2) вектор . Тогда модель (2) примет вид

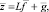(6)

где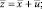

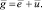
Матрицы нагрузок на общие факторы L в моделях (3) и (6) совпадают.

Вектор имеет многомерное нормальное распределение N(0, Σ₀), где Σ₀ = Σ + Δ.

Выберем диагональную матрицу Δ таким образом, чтобы S₀ – выборочная ковариационная матрица вектора 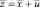стала положительно определенной и оценки дисперсий всех специфических факторов модели (6) стали отличными от нуля.

Выборочная ковариационная матрица S₀ вектора будет иметь распределение Уишарта w(Σ₀, n). Так как S₀ положительно определена, плотность распределения Уишарта в точке S₀ отлична от нуля [4]. Следовательно, для оценки матриц L и V₀ модели (6) применим метод максимального правдоподобия. Функцию максимального правдоподобия получим, заменив в (5) 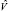на 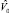, S на S₀ и 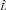на 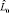. В силу выбора Δ оценки дисперсий специфических факторов положительны. Поэтому для максимизации функции правдоподобия можно воспользоваться любым из двух описанных в литературе подходов. При этом мы получим состоятельные, асимптотически несмещенные и эффективные оценки матриц L и V₀. Оценка матрицы нагрузок V на специфические факторы в модели (3) определяется из соотношения

.

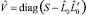В практических задачах часто приходится рассматривать в качестве исходной выборочную корреляционную, а не ковариационную матрицу переменных. В этом случае полученную оценку матрицы нагрузок на общие факторы вектора необходимо преобразовать, чтобы получить оценку матрицы нагрузок на вектор .

Пусть 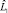– оценка матрицы нагрузок на общие факторы нормированного вектора , 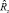и 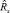– оценки корреляционных матриц нормированных векторов и соответственно.

Очевидно,

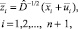(7)

где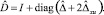

Из (7) получаем

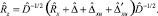
Считая 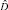не зависящей от выборки, легко показать, что

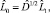
где 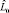– оценка матрицы L модели (6).

Оценка 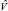вычисляется по формуле

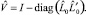
Оценка числа общих факторов

Для проверки гипотез о числе общих факторов используется статистика [4]

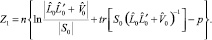
Так как матрицы S₀ и 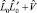не вырождены, то можно теперь для модели (6) проверить гипотезы о числе общих факторов.

Числа общих факторов в моделях (6) и (3) равны между собой.

Очевидно, при фиксированной матрице Δ, P_m → 1 по вероятности при n → ∞, где Р_m – вероятность принять гипотезу H₀ о числе общих факторов в модели (6), равном m.

Рассмотрим зависимость статистики Z₁ от выбора матрицы Δ при фиксированном объеме выборки.

Выборочная ковариационная матрица вектора равна

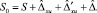(8)

Оценка максимального правдоподобия матрицы V₀ связана с S₀ и 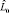соотношением [4]

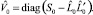(9)

Учитывая (8) и (9), нетрудно получить, что при .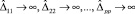

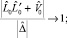
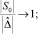(10)

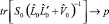(11)

по вероятности.

При Δ_jj → ∞ оценки 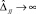по вероятности, откуда, с учетом соотношений (10) и (11), получаем, что статистика Z₁ при 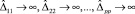стремится к нулю по вероятности. Следовательно, в этом случае P₀ → 1 по вероятности, где P₀ – вероятность принять гипотезу H₀ о том, что число общих факторов равно нулю.

Поскольку статистика Z₁ с ростом дисперсии «шума» убывает, при решении практических задач оценка числа общих факторов вследствие недостаточного объема выборки может оказаться заниженной. Поэтому численные значения Δ_jj следует выбирать не слишком большими, лишь бы только новые оценки дисперсий специфических факторов в модели (6) не получились равными нулю. Поскольку дисперсии оценок зависят от объема выборки, то и выбор численных значений Δ_jj будет зависеть в этом случае от объема выборки.

Факторный анализ направлен на анализ структуры внедиагональных элементов ковариационных матриц. Чем меньшие значения Δ_jj будут выбраны, тем меньше будут отличаться внедиагональные элементы выборочных ковариационных матриц S и S₀ и, следовательно, тем меньшее влияние на оценку матрицы нагрузок L окажет наложенный на статистические данные «шум» (при фиксированном объеме выборки). Это также является аргументом в пользу выбора небольших значений Δ_jj.

Случай вырожденного распределения

В практических исследованиях может встретиться ситуация, когда какая-то компонента вектора , например х₁, является линейной комбинацией остальных. Рассмотрим, как и выше, вектор и допустим, что Δ₁₁ > 0 (Δ₁₁ – дисперсия u₁). Тогда, если независимые переменные х₂, х₃,…, х_p имеют невырожденное многомерное нормальное распределение, то и вектор будет иметь невырожденное нормальное распределение и можно, таким образом, включить х₁ в факторную модель (6). Это дает большую свободу в отборе переменных для факторного анализа, а также может быть использовано при построении уравнения регрессии с помощью факторного анализа.

Рецензенты:

Кобелев Н.Б., д.э.н., профессор кафедры «Системный анализ и моделирование экономических процессов», Финансовый университет при Правительстве РФ, Президент НП «Ремесленная палата России», г. Москва;

Киселёва И.А., д.э.н., профессор кафедры «Прикладная математика», МЭСИ, г. Москва.

Библиографическая ссылка