Среди металлообрабатывающего оборудования можно выделить класс машин фигурной листовой резки с ЧПУ. К ним относятся машины термической (лазерной, плазменной, газовой резки) и гидроабразивной резки. Данные типы машин работают по управляющим программам (УП). Можно выделить ряд ограничений, которых придерживаются технологи при проектировании УП для машин данного типа.
Во-первых, перед началом вырезки заготовки необходимо врезаться в материал. Врезку необходимо расположить на некотором расстоянии от обрабатываемого контура для того, чтобы избежать «наплыва» материала на поверхность заготовки (рис. 1). Во-вторых, при термической и гидроабразивной обработке происходит «сгорание», «выметание» материала при обработке, поэтому при вырезке деталей необходимых размеров и геометрии контур обрабатываемой детали и движение инструмента не совпадают. Инструмент перемещается по эквидистанте этого контура (рис. 1).
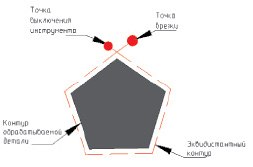
Рис. 1. Пример схемы резки по «замкнутому контуру»
В-третьих, необходимо учесть условие предшествования, которое обусловлено особенностями машин портального типа [3]. Если деталь содержит внутренний контур, то сначала необходимо вырезать его, а только потом внешний, т.к. после вырезки внешнего контура деталь может сместиться на рабочем столе. Также если на карте раскроя внутренний контур одной детали будет содержать внешний контур другой детали, то сначала вырезаем деталь, находящуюся внутри другой детали, а затем – внешнюю.
При подготовке УП пользуются различными способами резки, например стандартная резка (рис. 1), резка «змейкой», цепная резка и др. [1, 3, 4, 5, 6]. Применение того или иного способа может приводить к минимизации времени и стоимости обработки, которые рассчитываются по следующим формулам соответственно [1, 2, 3]:
Tcut = Loff/Voff + Lon/Von + N∙tpt; (1)
Fcost = Loff∙Coff + Lon∙Con + N∙Cpt, (2)
где Loff и Lon – длины холостых и рабочих переходов режущей головки соответственно; Voff и Von – соответственно скорость холостых и рабочих переходов; Coff и Con – стоимость единицы пути с отключенным и включенным режущим инструментом соответственно; N – количество точек врезок всей раскройной карты и tpt – время, которое приходится на одну точку врезки; Cpt – стоимость одной точки врезки.
В разделе 2 будет описана постановка задач минимизации стоимости и времени обработки. В разделе 3 рассматривается вопрос определения поправочных коэффициентов для скорости режущего инструмента на рабочем ходу и приводится формула целевой функции с учетом этих поправочных коэффициентов. Результаты, полученные в данной работе, приведены в заключении.
Задачи оптимизации маршрута инструмента машин термической и гидроабразивной резки с ЧПУ
В [3] была приведена формализация задач минимизации стоимости и времени обработки в виде задач дискретной оптимизации. Кратко рассмотрим постановку этих задач. Пример карты раскроя приведен на рис. 2.
Пусть N – количество контуров на карте раскроя, Mi = (xi, yi) и 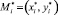 – соответственно точки врезки и точки отключения инструмента для i = 1, 2, ..., N,
– соответственно точки врезки и точки отключения инструмента для i = 1, 2, ..., N, 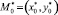 – исходная точка положения инструмента перед и после завершения обработки материала. Учитывая требования, описанные в разделе 1, последовательность вырезаемых контуров задаётся перестановкой I = (i1, i2, ... iN) порядка N. Таким образом, маршрут резки определяется вектором R размерности 5N [3]:
– исходная точка положения инструмента перед и после завершения обработки материала. Учитывая требования, описанные в разделе 1, последовательность вырезаемых контуров задаётся перестановкой I = (i1, i2, ... iN) порядка N. Таким образом, маршрут резки определяется вектором R размерности 5N [3]:
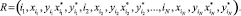 (3)
(3)
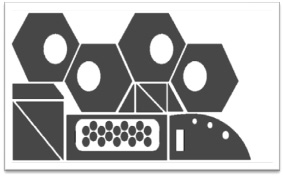
Рис. 2. Пример карты раскроя для 31 заготовки
Задачи оптимизации времени и стоимости обработки для заданной карты раскроя при применении стандартной техники резки сводятся к поиску векторов R, при которых целевые функции (1) и (2) достигают минимума. Запишем (1) и (2) с использованием обозначений элементов вектора R. Для этого введём дополнительные обозначения. Пусть 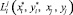 – расстояние, которое проходит режущая головка на холостом ходу при переходе от детали i к j (i, j = 0, 1, 2, …, N; i ≠ j),
– расстояние, которое проходит режущая головка на холостом ходу при переходе от детали i к j (i, j = 0, 1, 2, …, N; i ≠ j), 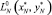 – расстояние, которое проходит режущая головка на холостом ходу после окончания обработки карты раскроя к исходному положению. Пусть также Pi – периметр эквидистантного контура с номером i,
– расстояние, которое проходит режущая головка на холостом ходу после окончания обработки карты раскроя к исходному положению. Пусть также Pi – периметр эквидистантного контура с номером i, 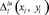 – расстояние перемещения резака из точки врезки Mi до эквидистантного контура и
– расстояние перемещения резака из точки врезки Mi до эквидистантного контура и 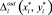 – расстояние перемещения резака от эквидистантного контура до точки отключения инструмента
– расстояние перемещения резака от эквидистантного контура до точки отключения инструмента 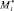 . Длины перемещений на холостом и рабочем ходе резака Loff и Lon могут быть записаны в следующем виде [3]:
. Длины перемещений на холостом и рабочем ходе резака Loff и Lon могут быть записаны в следующем виде [3]:
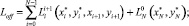 (4)
(4)
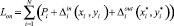 . (5)
. (5)
Предположим, что имеется конечное множество G1 множества допустимых значений G кортежа R. Пусть ki – число возможных врезок для контура i; K – общее число врезок для карты раскроя, 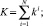 L1(is, jt) – расстояние между точкой отключения инструмента s контура i до врезки t контура j. Тогда (4) примет вид [3]:
L1(is, jt) – расстояние между точкой отключения инструмента s контура i до врезки t контура j. Тогда (4) примет вид [3]:
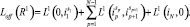 (6)
(6)
Если при подготовке УП задаются расстояние от врезки до эквидистантного контура i 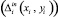 и длина перемещения от контура i до точки отключения инструмента
и длина перемещения от контура i до точки отключения инструмента 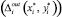 , то
, то 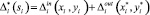 – сумма перемещений режущего инструмента от точки врезки до контура и от контура до точки отключения инструмента. Если у нас конечное число точек врезок, то (5) примет вид
– сумма перемещений режущего инструмента от точки врезки до контура и от контура до точки отключения инструмента. Если у нас конечное число точек врезок, то (5) примет вид
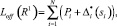
а (1) и (2) [3]:
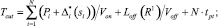 (7)
(7)
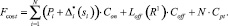 (8)
(8)
Влияние количества кадров УП и конфигурации обрабатываемого контура на скорость режущего инструмента
В целевой функции (1), (7) скорость рабочих перемещений режущей головки принята постоянной величиной. Но в результате проведенных ранее исследований и опыта установлено, что скорость обработки материала при увеличении количества кадров в УП снижается [7]. Поэтому встала задача о нахождении поправочных коэффициентов для величины Von в целевой функции (1), (7) [8].
Было проведено исследование для определения влияния количества кадров в УП, конфигурации вырезаемых контуров для лазерного комплекса ByStar 3015 [8]. По результатам были получены некоторые зависимости скорости режущего инструмента на рабочем ходу от количества кадров в УП и длины прямого реза (количества мелких/крупных контуров на раскройной карте) и поправочные коэффициенты для скорости режущего инструмента на рабочем ходу в целевой функции (1), (7) [8].
На рис. 3 можно увидеть, что с увеличением количества крупных деталей на раскройной карте скорость рабочего хода имеет тенденцию к возрастанию. Отсюда следует, что скорость на рабочем ходу при обработке деталей с различной геометрией и размерами не постоянна, и чем меньше мелких деталей, т.е. чем больше длина прямого реза, тем скорость выше (рис. 3) [8].
К зависимостям, приведенным в [8], были получены дополнительные зависимости скорости режущего инструмента на рабочем ходу от количества кадров n в УП и от длины прямого реза l для определенных условий (9)–(37). Ниже приведены зависимости скорости рабочего хода от количества кадров n в УП для сплава алюминия толщиной от 2 до 5 мм:
– для Амг3М t = 2 мм:
vp = –0,005∙ln(n) + 0,0728, (9)
с коэффициентом детерминации R2 = 0,9533;
– для Амг3М t = 3 мм:
vp = –0,002∙ln(n) + 0,033, (10)
с коэффициентом детерминации R2 = 0,9153;
– для Амг3М t = 5 мм:
vp = –9∙10–4∙ln(n) + 0,0193, (11)
с коэффициентом детерминации R2 = 0,9113.
В [8] было рассмотрено, как изменяется скорость резки, если вместо острого угла в обрабатываемой детали использовать скругления различного радиуса.
Из полученных данных следует, что с увеличением радиуса скруглений скорость рабочего хода незначительно, но увеличивается по отношению к контурам с прямыми углами (рис. 4, 5). Величина увеличения скорости рабочего хода зависит от значения радиуса скругления.
Ниже приведены зависимости скорости режущего инструмента на рабочем ходу от длины прямого реза l сплава алюминия толщиной от 1 до 3 мм:
1. С радиусом скругления прямых углов R = 1 мм по следующим формулам:
– для Амг3М t = 2 мм:
vp = 0,0044∙ln(l) + 0,0144, (12)
с коэффициентом детерминации R2 = 0,921;
– для Амг3М t = 3 мм:
vp = 0,0016∙ln(l) + 0,0134, (13)
с коэффициентом детерминации R2 = 0,9208.
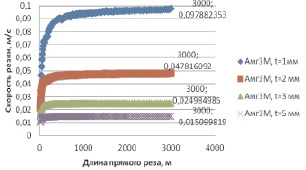
Рис. 3. Изменение скорости обработки при вырезке крупных и мелких контуров по раскройной карте
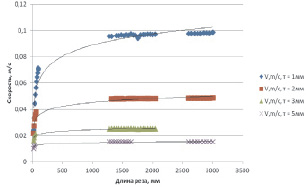
Рис. 4. Изменение скорости обработки заготовок типа прямоугольник с радиусом скруглений 2 мм по углам для Амг3М разной толщины для лазерного комплекса ByStar3015
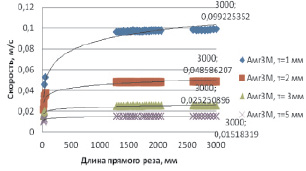
Рис. 5. Изменение скорости обработки заготовок типа прямоугольник с радиусом скруглений 5 мм по углам для Амг3М разной толщины для лазерного комплекса ByStar3015
2. С радиусом скругления прямых углов R = 2 мм по следующим формулам:
– для Амг3М t = 1 мм:
vp = 0,0123∙ln(l) + 0,0039, (14)
с коэффициентом детерминации R2 = 0,9353;
– для Амг3М t = 2 мм:
vp = 0,0043∙ln(l) + 0,0153, (15)
с коэффициентом детерминации R2 = 0,9185;
– для Амг3М t = 3 мм:
vp = 0,0016∙ln(l) + 0,0136, (16)
с коэффициентом детерминации R2 = 0,9147.
3. С радиусом скругления прямых углов R = 5 мм по следующим формулам:
– для Амг3М t = 1 мм:
vp = 0,014∙ln(l) – 0,0087, (17)
с коэффициентом детерминации R2 = 0,9654;
– для Амг3М t = 2 мм:
vp = 0,0043∙ln(l) + 0,0156, (18)
с коэффициентом детерминации R2 = 0,9144;
– для Амг3М t = 3 мм:
vp = 0,0017∙ln(l) + 0,0127, (19)
с коэффициентом детерминации R2 = 0,9114;
4. С радиусом скругления прямых углов R = 10 мм по следующим формулам:
– для Амг3М t = 1 мм:
vp = 0,0094∙ln(l) + 0,0269, (20)
с коэффициентом детерминации R2 = 0,9564;
– для Амг3М t = 2 мм:
vp = 0,0027∙ln(l) + 0,0277, (21)
с коэффициентом детерминации R2 = 0,9171;
– для Амг3М t = 3 мм:
vp = 0,0008∙ln(l) + 0,0194, (22)
с коэффициентом детерминации R2 = 0,9229;
Ниже приведены зависимости скорости режущего инструмента на рабочем ходу от количества кадров n в УП для сплава алюминия толщиной от 2 до 5 мм:
1. С радиусом скругления прямых углов R = 1 мм по следующим формулам:
с коэффициентом детерминации R2 = 0,9413;
– для Амг3М t = 2 мм:
vp = –0,005∙ln(n) + 0,0671, (23)
с коэффициентом детерминации R2 = 0,9049;
– для Амг3М t = 3 мм:
vp = –0,001∙ln(n) + 0,0312, (24)
с коэффициентом детерминации R2 = 0,8504;
– для Амг3М t = 5 мм:
vp = –7∙10–4∙ln(n) + 0,0182, (25)
с коэффициентом детерминации R2 = 0,8408.
2. С радиусом скругления прямых углов R = 2 мм по следующим формулам:
– для Амг3М t = 1 мм:
vp = –0,015∙ln(n) + 0,1588, (26)
с коэффициентом детерминации R2 = 0,9666;
– для Амг3М t = 2 мм:
vp = –0,005∙ln(n) + 0,0683, (27)
с коэффициентом детерминации R2 = 0,9168;
– для Амг3М t = 3 мм:
vp = –0,001∙ln(n) + 0,0313, (28)
с коэффициентом детерминации R2 = 0,8714;
– для Амг3М t = 5 мм:
vp = –7∙10–4∙ln(n) + 0,0183, (29)
с коэффициентом детерминации R2 = 0,8589.
3. С радиусом скругления прямых углов R = 5 мм и 10 мм соответственно по следующим формулам:
– для Амг3М t = 1 мм:
vp = –0,015∙ln(n) + 0,1613, (30)
с коэффициентом детерминации R2 = 0,9586;
– для Амг3М t = 2 мм:
vp = –0,005∙ln(n) + 0,068, (31)
с коэффициентом детерминации R2 = 0,905;
– для Амг3М t = 3 мм:
vp = –0,002∙ln(n) + 0,0317, (32)
с коэффициентом детерминации R2 = 0,8488;
– для Амг3М t = 5 мм:
vp = –8∙10–4∙ln(n) + 0,0185, (33)
с коэффициентом детерминации R2 = 0,8345;
– для Амг3М t = 1 мм:
vp = –0,013∙ln(n) + 0,1534, (34)
с коэффициентом детерминации R2 = 0,9342;
– для Амг3М t = 2 мм:
vp = –0,004∙ln(n) + 0,0649, (35)
с коэффициентом детерминации R2 = 0,9229;
– для Амг3М t = 3 мм:
vp = –0,001∙ln(n) + 0,03, (36)
с коэффициентом детерминации R2 = 0,9112;
– для Амг3М t = 5 мм:
vp = –6∙10–4∙ln(n) + 0,0175, (37)
с коэффициентом детерминации R2 = 0,8945.
В [8] приведены таблицы значений поправочного коэффициента для скорости режущего инструмента на рабочем ходу для лазерного комплекса ByStar 3015 в зависимости от длины прямого реза для сплава АМг3М толщиной от 1 до 5 мм.
Также значение поправочного коэффициента с определенной погрешностью можно найти, используя зависимости (9)–(37). Таким образом, полученные поправочные коэффициенты k для скорости рабочих перемещений режущей головки для лазерного комплекса ByStar 3015 можно подставить в целевую функцию (7), которая примет вид
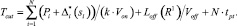 (38)
(38)
Для решения этой задачи можно воспользоваться математической моделью А.Г. Ченцова [9], которая позволяет, по сравнению с известными алгоритмами, учитывать дополнительные ограничения термической и гидроабразивной резки.
Заключение
Основные результаты, полученные в данной работе:
1. Приведены ограничения и особенности термической и гидроабразивной резки, которые необходимо учитывать при решении поставленных задач.
2. Приведена формализация задач оптимизации маршрута инструмента для машин фигурной резки листового материала.
3. По результатам исследований были получены поправочные коэффициенты для скорости рабочего хода режущего инструмента и целевая функция была записана с учетом этих коэффициентов.
4. Для решения этих задач можно воспользоваться моделью А.Г. Ченцова, которая позволяет учесть особенности термической и гидроабразивной резки.
В дальнейшем планируется расширить область исследования зависимости скорости обработки для другого типа материала для контуров прямоугольного типа, а также получить поправочные коэффициенты для контуров фигурного типа.
Рецензенты:
Комиссаров А.П., д.т.н., профессор кафедры горных машин и комплексов, ФГБОУ ВПО «Уральский государственный горный университет», г. Екатеринбург;
Кожушко Г.Г., д.т.н., профессор кафедры подъемно-транспортных машин, ФГАОУ ВПО «Уральский федеральный университет», г. Екатеринбург.
Библиографическая ссылка
Петунин А.А., Таваева А.Ф. ОБ ОПТИМИЗАЦИИ МАРШРУТА ИНСТРУМЕНТА ДЛЯ МАШИН ФИГУРНОЙ ЛИСТОВОЙ РЕЗКИ С ЧПУ ПРИ УСЛОВИИ НЕПОСТОЯНСТВА СКОРОСТИ РАБОЧЕГО ХОДА // Фундаментальные исследования. 2015. № 6-1. С. 56-62;URL: https://fundamental-research.ru/ru/article/view?id=38393 (дата обращения: 28.02.2026).



