К настоящему времени аппаратный облик цифровых систем управления авиационных газотурбинных двигателей (САУ ГТД) определился в виде двухканальной (дублированной) схемы с «полной ответственностью». Требование дальнейшего повышения надежности системы выполняется путем не аппаратного (троирование, квадрирование), а алгоритмического резервирования. С этой целью в САУ встраивается математическая модель двигателя, позволяющая выполнять не только функции определения отказов информационных каналов, но и замещения информации отказавших каналов. Эта бортовая встроенная математическая модель двигателя (ВММ ГТД) принадлежит к особому классу моделей в силу специфических требований к ней: надежная работа в реальном масштабе времени (а следовательно, высокое быстродействие – частота выдачи решения 50 Гц), ограниченный объем памяти (объем порядка 100 КБ) при сохранении достаточно высоких требований к точности отображения в статике и динамике в большом диапазоне режимов работы, полетных условий и состояний двигателя [1]. При этом важным условием выполнения требований точности является обеспечение корректности управляющего сигнала на входе ВММ, что достигается и идентификацией неисправности информационных каналов.
Целью исследования является анализ точности разработанных алгоритмов идентификации входных информационных потоков ВММ ГТД, основанных на методах Калман-фильтрации со встроенной логикой обнаружения отказа измерительного канала.
Материалы и методы исследования
Поскольку одной из приоритетных задач систем автоматического управления (САУ) ГТД является обеспечение стабильности параметров работы двигателя, путем корректного дозирования подачи топлива (расхода топлива – GT) в основную камеру сгорания, для обеспечения надежности входной информации ВММ ГТД производится фильтрация входных информационных потоков, для чего строится отказоустойчивый блок фильтрации, включающий математическую модель канала дозирующей иглы (ДИ). Математическая модель ДИ позволяет получить расчетные данные о расходе топлива по заданному значению положения поршня ДИ 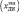 . Выходным сигналом модели ДИ является прогнозируемое (модельное) значение положения поршня – xДИ. При этом передаточная функция ДИ имеет вид
. Выходным сигналом модели ДИ является прогнозируемое (модельное) значение положения поршня – xДИ. При этом передаточная функция ДИ имеет вид
 (1)
(1)
Учитывая, что САУ ГТД работает в условиях помех, как в канале модели (обусловленных ее неточностью), так и в канале измерения (обусловленных погрешностью измерителей – датчиков), для обеспечения надежности идентификации управляющего сигнала GT на выходе модели ДИ подключен рекурсивный фильтр Калмана, основным свойством которого является его способность к адаптации – самокоррекции в процессе фильтрации данных. Алгоритмы самокоррекции строятся на определении в текущий момент tk оптимального коэффициента Калмана (Kk) в результате решения задачи минимизации математического ожидания квадрата ошибки идентифицируемого параметра 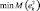 с учетом оптимальной оценки в предыдущий момент. Коэффициент Калмана задает вероятностное соотношение модельной и измеренной составляющих в оптимальном значении идентифицируемого xДИ. Алгоритм Калман-фильтрации [2] включает вычисление на каждом шаге:
с учетом оптимальной оценки в предыдущий момент. Коэффициент Калмана задает вероятностное соотношение модельной и измеренной составляющих в оптимальном значении идентифицируемого xДИ. Алгоритм Калман-фильтрации [2] включает вычисление на каждом шаге:
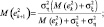
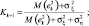 (2)
(2)
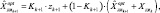 (3)
(3)
где 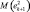 – минимальное значение математического ожидания квадрата ошибки; ξk, ηk – ошибки модели и датчика; Kk+1 – коэффициент Калмана;
– минимальное значение математического ожидания квадрата ошибки; ξk, ηk – ошибки модели и датчика; Kk+1 – коэффициент Калмана; 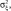
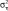 – дисперсии модели и датчика;
– дисперсии модели и датчика; 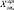 – оптимальная оценка идентифицируемой величины перемещения поршня; zk – показание датчика перемещения поршня;
– оптимальная оценка идентифицируемой величины перемещения поршня; zk – показание датчика перемещения поршня; 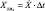 – приращение перемещения поршня, полученное на (k + 1)-м шаге с помощью разработанной математической модели ДИ.
– приращение перемещения поршня, полученное на (k + 1)-м шаге с помощью разработанной математической модели ДИ.
Совместное решение дифференциальных уравнений (2)–(3) позволило определить передаточную функцию фильтра Калмана:
WФК(p) = 1. (4)
Возможность применения алгоритма Калман-фильтрации для решения рассматриваемой задачи обусловлена нормальностью распределения случайных величин и эргодичностью случайных процессов в каналах управления и измерения, доказанными на основе статистической обработки данных натурных испытаний двигателя [3].
Как показано выше, качество фильтрации во многом определяется валидностью используемых в вычислениях измерений перемещения поршня. Реализуемое на практике аппаратное резервирование предусматривает дублирование измерений с помощью двухканальной системы датчиков. В этой связи актуальной задачей является обеспечение надежной идентификации неисправных информационных каналов, для чего предлагается в алгоритмы Калман-фильтрации включать дополнительную логику обнаружения и локализации отказа (ОЛО) канала датчика, обеспечивающую повышение надежности [4].
Неисправности датчика относят к так называемыми «мягким» отказам, характеризующимся относительно небольшим расхождением между истинным и измеренным значениями, поэтому их трудно обнаружить с помощью обычной проверки рабочего диапазона. Предлагается для оценки точности измерения группы датчиков использовать банки фильтров Калмана [5], позволяющие генерировать вектор (матрицу-столбец) отклонений:
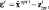 (5)
(5)
где для i-датчика εi – ошибка оценки;  – оптимальная оценка (на выходе соответствующего фильтра Калмана);
– оптимальная оценка (на выходе соответствующего фильтра Калмана); 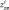 – измеренное значение перемещения поршня.
– измеренное значение перемещения поршня.
Для идентификации отказа датчиков вычисляется взвешенная сумма квадратов отклонений WSSR (Weighted Sum of the Squares of Residuals) которую называют также признаком или сигнатурой отказа [6] – с помощью матричного уравнения
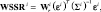 (6)
(6)
где 
Вектор σi представляет стандартные (паспортные) отклонения i-датчика и нормирует вектор отклонений. Скалярный весовой коэффициент Wr является параметром инженерной настройки, и его выбирают таким образом, чтобы уровень WSSR-сигнала был меньше заданного порогового значения в номинальном состоянии, когда все датчики исправны.
Следует отметить, что при Wr = 1 и равенстве εi = σi WSSR равен числу датчиков в рассматриваемой группе. Для случая εi ≠ σi применима упрощенная формула
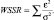 (7)
(7)
Тогда для одного канала двухканального датчика справедливо
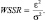 (8)
(8)
Поэтому чем меньше сигнатура отказа, тем меньше вероятность отказа датчика.
В предлагаемой разработке сигнал сигнатуры отказа вырабатывается на основе сравнения текущего измерения обоих каналов zди l (l = 1, 2) и оптимальной оценки величины перемещения поршня 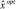 на предыдущем шаге с помощью алгоритма обнаружения и локализации отказа (ОЛО) каналов измерения, встраиваемого в алгоритм Калман-фильтрации.
на предыдущем шаге с помощью алгоритма обнаружения и локализации отказа (ОЛО) каналов измерения, встраиваемого в алгоритм Калман-фильтрации.
Для обнаружения неисправности датчика WSSR сравнивается с пороговым значением, величина которого выбирается путем экспертной оценки на основе статистической обработки экспериментальных данных для индивидуального двигателя. Следует учитывать, что малая величина порогового значения может привести к ложным срабатываниям, большая – к необнаружению отказов. Ряд специалистов [4, 6] рекомендуют задавать сигнатуру отказа в диапазоне [1.5; 2]. В данном исследовании был выбран порог, равный 2. Алгоритм обнаружения и локализации отказа (ОЛО) канала датчика хода поршня иллюстрируется табл. 1.
С выхода отказоустойчивого блока фильтрации (со встроенным алгоритмом ОЛО) сигнал хода поршня поступает на дифференциальный клапан (регулятор перепада давления), математическая модель которого строится на соотношениях
 и
и 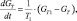 (9)
(9)
где T1 = 0,05 с, а зависимости ∆GT = f(Xди), GT1 = f(Xди) задаются в виде экспериментальных таблиц. Выходным параметром дифференциального клапана является расход топлива GT, который поступает на вход ВММ ГТД.
Результаты исследования и их обсуждение
Результаты моделирования в среде MatLab ситуаций, когда оба измерительных канала двухканального датчика исправны (в качестве выходного сигнала ОЛО берется сигнал с датчика с меньшим WSSR) и при отказе второго канала, наступившем в момент t = 3,2 с (в качестве выходного сигнала берется сигнал с исправного канала), приведены на рис. 1.
Таблица 1
Алгоритм обнаружения и локализации отказа канала двухканального датчика
|
WSSR1 |
WSSR2 |
Ситуация |
На выход поступает |
|
≤ 2 |
≤ 2 |
Оба канала исправны |
Отфильтрованное xДИ, канала с minWSSR |
|
≤ 2 |
≥ 2 |
Отказ второго канала |
Отфильтрованное (по Калману) xДИ первого канала |
|
≥ 2 |
≤ 2 |
Отказ первого канала |
Отфильтрованное (по Калману) xДИ второго канала |
|
≥ 2 |
≥ 2 |
Оба канала отказали |
Модельное значение xДИ |
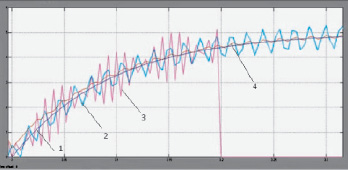
Рис. 1. Результаты моделирования в среде MatLab ситуаций, когда оба измерительных канала двухканального датчика исправны и при неисправности второго канала: 1 – модельное значение, 2, 3 – измерение первого и второго канала, 4 – выходной сигнал
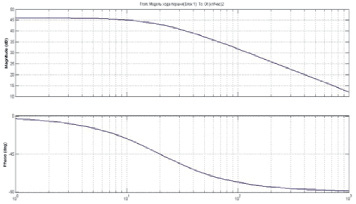
Рис. 2. ЛАЧХ и ЛФЧХ части блока ввода информации в ВММ, полученные в MatLab
Важным показателем надежности системы является ее устойчивость, определяемая видом частотных характеристик систем.
Результаты моделирования в среде MatLab логарифмических амплитудо- и фазочастотных характеристик (ЛАЧХ и ЛФЧХ) соединения элементов, включающего фильтр Калмана со встроенным блоком ОЛО и дифференциальный клапан (регулятор перепада давления), приведены на рис. 2. На вход последовательного соединения элементов подается сигнал – Хди с выхода математической модели ДИ, на выходе – сигнал расхода топлива GT.
Полученные в результате модельного эксперимента ЛАЧХ и ЛФЧХ соответствуют классическому апериодическому звену первого порядка с параметрами:
– коэффициент усиления определяется из 20.lgk = 46 дБ и равен k = 199,53 ≈ 200;
– постоянная времени
T2 = 1/ω2 = 1/20 = 0,05 с;
– наклон ЛАЧХ при ω > ω1 равен – 20 дБ/дек;
– частота среза определяется из L(ωср) ≈ 20lg(k/Twср) = 0 и равна ωср = k/T ≈ 4∙103 рад/с;
– фаза на всем диапазоне частот изменяется от 0 до –90°;
– величина фазы на частоте среза
(wср)= –arctg(T1wср) = –89,71°.
Передаточная функция рассматриваемого соединения элементов совпадает с передаточной функцией дифференциального клапана (регулятора перепада давления):
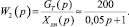 (10)
(10)
Это подтверждает правильность аналитических преобразований, позволивших вычислить передаточную функцию фильтра Калмана в виде (4). Кроме того, результаты модельного эксперимента позволяют утверждать, что
WОЛО (p) = 1. (11)
Общая передаточная функция отказоустойчивого блока ввода входной информации ВММ ГТД равна:
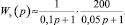 (12)
(12)
Поскольку корни характеристического уравнения рассматриваемого блока ввода p1 = –10 с–1, p2 = –20 с–1 – действительны и отрицательны, он является апериодическим звеном второго порядка. ЛАЧХ и ЛФЧХ отказоустойчивого блока ввода информации представлены на рис. 3.
Параметры отказоустойчивого блока ввода информации:
– коэффициент усиления определяется из 20lgk = 46дБ и равен k = 199,53 (≈ 200);
– постоянные времени
T2 = 1/ω2 = 1/20 = 0,05;
T1 = 1/ω1 = 1/10 = 0,1;
– наклон ЛАЧХ при ω1 < ω < ω2 равен –20 дБ/дек, при ω > ω2 равен –40 дБ/дек;
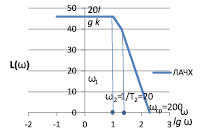
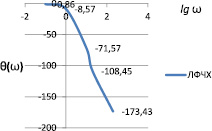
Рис. 3. ЛАЧХ и ЛФЧХ отказоустойчивого блока ввода входной информации ВММ
Следует отметить, что рассмотренный блок охвачен через САУ обратной связью, что повышает его запас устойчивости.
– частота среза определяется из
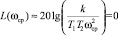
и равна ωср ≈ 200 рад/с;
– фаза на всем диапазоне частот изменяется от 0 до –180°;
– величина фазы на частоте среза
θ(ωср) = –(arctg(T1ωср) + arctg(T2ωср)) = –173,43°.
Выводы
Важным результатом проведенного исследования частотных свойств является доказательство равенства единице коэффициента усиления разработанного отказоустойчивого блока фильтрации и отсутствия дополнительных фазовых сдвигов, внесенных возможным чистым запаздыванием, обусловленным особенностями реализуемых алгоритмов обнаружения отказов измерительных каналов и Калман-фильтрации входной информации ВММ. Тем самым доказывается отсутствие их влияния на устойчивость САУ ГТД.
Апробация разработанных алгоритмов показала, что средняя относительная ошибка динамики составляет 0,168 %, которая в статике при максимальном расходе Gт = 3800 кг/ч снижается до 0,01 %, что соответствует современным требованиям точности алгоритмов идентификации по контуру ДИ.
Все это подтверждает работоспособность и практическую ценность разработанных алгоритмов.
Рецензенты:
Труфанова Н.М., д.т.н., профессор, зав. кафедрой конструирования и технологий в электротехнике, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Кавалеров Б.В., д.т.н., доцент, зав. кафедрой «Электротехника и электромеханика», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Библиографическая ссылка
Кузнецова Т.А., Губарев Е.А. ОТКАЗОУСТОЙЧИВЫЕ АЛГОРИТМЫ ИДЕНТИФИКАЦИИ ВХОДНОЙ ИНФОРМАЦИИ БОРТОВОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ В СОСТАВЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АВИАЦИОННОГО ДВИГАТЕЛЯ // Фундаментальные исследования. 2015. № 6-1. С. 39-43;URL: https://fundamental-research.ru/ru/article/view?id=38390 (дата обращения: 09.01.2026).



