Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кобрунов А.И. 1 Мотрюк Е.Н. 1 Ломинский Д.О. 2

---

1 ФГБОУ ВПО «Ухтинский государственный технический университет»

2 ФГБОУ ВПО «Российский государственный университет нефти и газа имени И.М. Губкина»

Проведено исследование сходимости алгоритма односторонней интерполяции для восстановления объемной среды по системе профилей, который позволяет максимально учитывать априорную информацию о геолого-геофизических параметрах среды. Вычислительные схемы построения объемной структурно-плотностной модели геологической среды созданы для использования их при решении прямых и обратных задач гравиразведки и протестированы на модельных примерах. Шаг интерполяции границ следует выбирать таким, чтобы он мог учитывать особенности геологической среды с достаточной для решения последующих задач точностью, а также близким к шагу, с которым задаются исходные данные. Нижняя граница выбора шага зависит от вида работ. Существенно влияет на результат построения также выбор расчетных линий в пределах участка. Он определяется положением интересующей нас аномалии. Расчетная линия должна проходить через центральную часть наиболее интересующей нас аномалии, вкрест ее простирания. С учетом сделанных замечаний процесс интерполяции является устойчивым и может применяться для моделирования геологических сред сложного строения.

Статья в формате PDF

511 KB

гравиразведка

сложнопостроенные среды

прямые задачи гравиразведки

метод интерполяции границ

модель геологической среды

сходимость алгоритма

Аминов Л.З., Кобрунов А.И., Моисеенкова С.В., Мотрюк Е.Н., Шилова С.В., Мужикова А.В. Методика интегрированной интерпретации гравиметрических данных в условиях слабой изученности с целью построения объемных региональных плотностных моделей седиментационных бассейнов / Геология и минеральные ресурсы Европейского Северо-востока России: материалы XIV геологического съезда Республики Коми. Том IV. – Сыктывкар: Геопринт, 2004. – С. 79–81.

Кобрунов А.И. Алгоритм учёта влияния вмещающей среды при инверсии гравиметрических данных / А.И. Кобрунов, М.И. Барабанов // Известия Коми НЦ УрО РАН. – 2014. – № 1 (17). – С. 84–88.

Кобрунов А.И. Математические методы моделирования в прикладной геофизике (избранные главы) в 2-х частях. Ч.1 Функционально-аналитические основы // Международный журнал экспериментального образования. – 2014. – № 11, ISSN – 199-3947. 78 с. Ч. 2 Системный анализ и моделирование в условиях неопределенности. – Ухта, УГТУ, 2014. – 154 с.

Кобрунов А.И., Петровский А.П., Даниленко А.Н., Моисеенкова С.В., Аминов Л.З. Теория и методы количественной комплексной интерпретации геофизических данных // Актуальные научно-технические проблемы развития геолого-геофизических промысловых и поисково-разведочных работ в Республике Коми. Книга 1. – Ухта, 2001. – С. 261–316.

Кобрунов А.И. Математические основы теории интерпретации геофизических данных: учеб. пособие. – Ухта: УГТУ, 2007. – 286 с.: ил.

Мотрюк Е.Н., Мужикова А.В. Объемное структурно-плотностное моделирование геологической среды методом односторонней интерполяции на примере тел простейшей формы // Севергеоэкотех – 2003: материалы IV Межрегиональная молодежная научная конференция. – Ухта, УГТУ, 2003. – С. 554–556.

Мотрюк Е.Н., Мужикова А.В., Шилова С.В. Методика выбора аппроксимации для решения прямой задачи гравиразведки // Севергеоэкотех – 2002: тезисы докладов Межрегиональная молодежная научная конференция. – Ухта, 2002. – С. 31–32.

Прогноз нефтегазоносности требует наличия объемной структурно-плотностной модели геологической среды, удовлетворяющей гравитационному полю. Однако для построения имеются только фрагментарно заданные данные. Построенные двумерные модели могут быть реконструированы решением структурной или плотностной обратных задач гравиразведки [1–5]. Для преобразования двумерных данных в трехмерные существует много прикладных программных средств (например, Surfer, Коскад 3D и др.), алгоритмов (послойной интерполяции, методы крайгинга и др.), выбор которых зависит от характера имеющихся данных. К тому же для реальных геологических сред погрешности, лежащие в основе этих продуктов, могут быть велики и сильно влиять на качество модели. В данной работе представлена апробация алгоритмов и вычислительных схем односторонней интерполяции профильных данных в объемные плотностные модели для случая сложнопостроенных сред. Их основные положения изложены в [6, 7]. Для установления точности вычислительных схем разработанной интерполяции геологических границ написана программа GRAST на языке Си++.

Модель среды

Модель среды представляет собой призму слоистой структуры, состоящую из трех пластов с плотностями σ₀ = 2,6 г/cм³, σ₁ = 3,0 г/cм³ и σ₂ = σ₀ = 2,6 г/cм³. Источником гравитационной аномалии является второй пласт, включающий в себя шар радиуса R = 2500 м, расположенный в центре призмы. Нижняя граница призмы 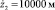, верхняя 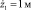(рис. 1). Тестирование интерполяции проведено на трех вариантах расположения профилей, в статье приведен один вариант. В природе не встречаются такого вида аномалии, чаще всего они типа уступа, так как геологическая среда слоистая ввиду своего вида образования. Значит, в нашем случае все вычисления будут давать большее значение погрешности построения, чем для реального объекта. Шаг интерполяции призмы step_x = step_y принимает значения 100, 250, 300, 400, 400, 600, 800, 1000 м. В результате получается пространственная сетка K = {(x, y, z): x, y ∈ (10000, 30000), z ∈ (1, 10000)}. Шаг, с которым заданы значения границ по профилям step_r = 250 м.

Модель задачи

При расчете значений глубин использовались формулы, выведенные для односторонней интерполяции границ в [6, 7]. Для вычисления точных значений глубин на сфере используем уравнение

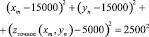
и уравнение прямой 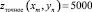в противном случае (вне сферы).

Для характеристики полученной при помощи односторонней интерполяции границы рассмотрим среднеквадратическое отклонение точных и рассчитанных значений при разном шаге интерполяции step_x:

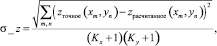(1)

где K_x + 1, K_y + 1 – количество координат x и у сетки K.

Очевидно, что при step_x ≤ step_r интерполяция будет иметь хорошую точность, так как будет учитывать исходную информацию с меньшими погрешностями. Таким образом, нам необходимо определить верхнюю рамку для step_x, его зависимость от шага step_r, при которой интерполяция будет отвечать заданной точности. Проведем интерполяцию второй геологической границы для разного расположения профилей.

Модель

Задано восемь тестируемых профилей, занумерованных 1–8 (рис. 2). Особенностью расположения профилей является то, что 7 и 8 профили имеют диагональную направленность, а остальные параллельны линиям сетки интерполяции.

Граница, представленная на рис. 3, не является симметричной относительно центра поверхностью, поскольку не все заданные координаты профилей совпадают с узлами сетки K. Граница имеет более округлый вид, чем в моделях 1 и 2, потому что в данном случае используется больше геолого-геофизической информации. В этом случае погрешность вычисленной границы (рис. 7–8) равна 2,3 м, что составляет 0,09 % от амплитуды рассматриваемой границы. Граница, представленная на рис. 4, не является симметричной относительно центра поверхностью, поскольку не все заданные координаты профилей совпадают с узлами сетки K. В этом случае погрешность вычисленной границы (рис. 3–4) равна 2,7 м и составляет 0,09 % от амплитуды рассматриваемой границы.

В случае, представленном на рис. 5, погрешность вычисленной границы (см. рис. 7–8) равна 6,4 м и составляет 0,26 % от амплитуды рассматриваемой границы. Граница, представленная на рис. 6, не является симметричной относительно центра поверхностью, поскольку не все заданные координаты профилей совпадают с узлами сетки K и к тому же очень велик шаг интерполяции.

Таким образом, для Модели 2 наилучшим шагом интерполяции для step_r = 250 м является шаг step_x до 800 м (что в 3,2 больше step_r), для step_r = 500 м – step_x до 800 м (что в 1,6 больше step_r). Далее отклонение от аппроксимирующей график невязки тренда-функции будет возрастать и иметь непредвиденные скачки.

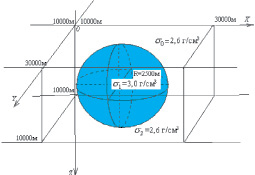
Рис. 1. Тестируемая модель

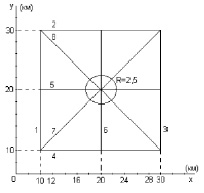
Рис. 2. Сечение Модели 3 плоскостью z = 5000 м

Рис. 3. Результаты интерполяции второй границы Модели 3 при step_x = 250

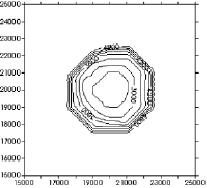
Рис. 4. Результаты интерполяции второй границы Модели 3 при step_x = 300

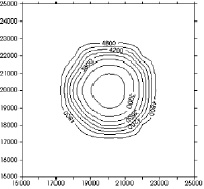
Рис. 5. Результаты интерполяции второй геологической границы Модели 3 при step_x = 800

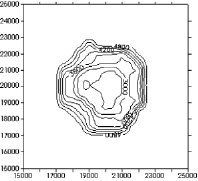
Рис. 6. Результаты интерполяции второй геологической границы Модели 3 при step_x = 500, step_r = 1000

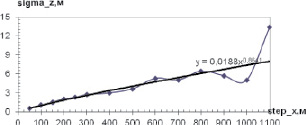
Рис. 7. График зависимости среднеквадратической погрешности исходной и интерполируемой границ от step_x при step_r = 250 м

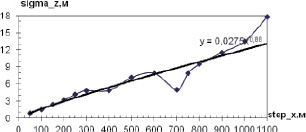
Рис. 8. График зависимости среднеквадратической погрешности исходной и интерполируемой границ от step_x при step_r = 500 м

Из графиков, представленных на рис. 7, 8, невязка в 5 мГал достигается при step_x = 670 м для step_r = 250 м, при step_x = 400 м для step_r = 500 м. При увеличении числа профилей в 1,3 раза фиксированное значение невязки достигается при шаге step_x, большем в 3,35 (при step_r = 250 м) и 2,66 (при step_r = 250 м) раза относительно исходного. Этот факт показывает, насколько важно для получения наиболее близкой к реальной среде модели использовать как можно больше геолого-геофизической информации.

Проведенные выше исследования позволяют сказать, что шаг интерполяции границ следует выбирать таким, чтобы он мог учитывать особенности геологической модели с достаточной для решения последующих задач точностью. Шаг, с которым происходит интерполяция исходных данных, лучше брать близким к шагу, с которым исходные данные задаются для интерполяции, до увеличения в 1,6 раз. Нижняя граница выбора step_x зависит от вида работ. Например, для детальных допустим самый маленький шаг step_x – 50 м, что для региональных исследований применять нецелесообразно. Существенно влияет на результат построения также выбор расчетных линий в пределах участка. Он определяется положением интересующей нас аномалии. Расчетная линия должна проходить через центральную часть наиболее интересующей нас аномалии, вкрест ее простирания. С учетом сделанных замечаний процесс интерполяции является устойчивым и может применяться для моделирования геологических сред сложного строения. Таким образом, разработанная интерполяционная процедура может использоваться для объемного моделирования осадочных бассейнов. Созданные способы восстановления объемной среды по системе профилей (односторонняя, «змейка», рекурсия) позволяют максимально учитывать априорную информацию о геолого-геофизических параметрах среды.

Рецензенты:

Бурмистрова О.Н., д.т.н., заведующая кафедрой технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;

Андронов И.Н., д.т.н., профессор кафедры сопротивления материалов и деталей машин, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.

Библиографическая ссылка