Метод преломленных волн (МПВ) успешно применяется в настоящее время для изучения упругих свойств грунтов (инженерная сейсморазведка) и строения земной коры. Он основан на использовании информации, содержащейся в записях головных волн. Эти волны возникают на границах между слоями, различающимися по значениям скоростей распространения в них упругих волн. При значении скорости упругих волн ниже границы (V2) большем, чем в слоях выше границы (V1), и определенном угле падения волн на эту границу возникает преломленная волна, скользящая вдоль границы, которая приводит к образованию восходящих к поверхности наблюдений головных волн.
Кинематические особенности головных волн хорошо изучены. Разработаны теория годографов головных волн и способы определения скоростного строения среды по этим годографам. Однако, содержащаяся в сейсмограммах информация о динамике (энергии) этих волн используется недостаточно (Телегин, 2004).
При кинематической интерпретации для получения сведений о скоростях в слоях и их геометрических параметрах (мощностях слоев, глубинах до границ, углах наклона границ) с сейсмограммы снимаются значения времен первых вступлений головных волн. Это является сложной и трудоемкой операцией, выполняемой вручную.
В статье на основе комплексного кинематического и динамического подхода к интерпретации сейсмограмм, получаемых при работах МПВ, предлагается оригинальный способ преобразования этих сейсмограмм в глубинные или временные сейсмические изображения геологической среды.
Постановка задачи
Ставится задача создания технологии совместного использования кинематической и динамической информации, содержащейся в сейсмограммах МПВ для автоматического получения сейсмических изображений среды. Подобно временным разрезам, получаемым в методе общей глубинной точки (МОГТ), эти изображения должны нести информацию о распределении упругих параметров (коэффициентов преломления) в изучаемом геологическом разрезе.
Значения параметров систем наблюдений, а также скоростные и геометрические характеристики среды выбраны типичными для инженерно-сейсмических работ при инженерно-геологических изысканиях.
Решение задачи основано на том предположении, что наблюдаемое сейсмическое волновое поле является суммарным полем волн дифракторов – объектов в среде, имеющих размеры, весьма малые по сравнению с длиной сейсмической волны. С этими объектами связаны явления дифракции сейсмических волн (Козлов, 2004).
В работе в качестве кинематической сейсмической модели среды (для расчета годографов и кинематических поправок) использовалась традиционно рассматриваемая модель, которая включает в себя однородные слои, блоки, границы между ними. То есть те элементы, которыми можно моделировать слоистость в разрезе, поверхности несогласия, области и границы тектонических нарушений, пустоты и каверны и т.п. При динамическом моделировании среда представлялась совокупностью расположенных на границах дифракторов.
Структура исходного волнового поля
Наличие одинаковой структуры элементарных полей дифракторов позволяет сравнительно легко изучать положение и относительную интенсивность источников этих полей и выполнять построение изображения источников поля (дифракторов) в геологическом разрезе. При этом должны быть известны правила, по которым образуется наблюдаемое волновое поле из полей волн, создаваемых расположенными в среде дифракторами.
К основным типам волн, наблюдаемым на сейсмограмме, относятся прямые, головные, рефрагированные, отраженные, кратные, поверхностные и дифрагированные волны. Все эти волны за исключением поверхностных могут быть еще продольными, поперечными или обменными. Обычно система наблюдений обеспечивает преимущественную регистрацию только монотипных и чаще всего продольных волн. Поэтому во всех примерах мы будем предполагать, что получены записи продольных волн. Переход к поперечным или обменным волнам сводится только к замене значений скоростей и не создает сложностей.
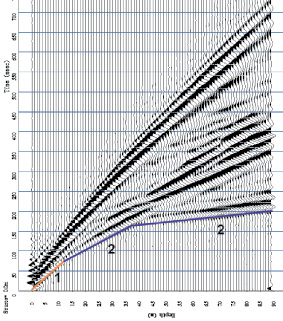
Рис. 1. Положение осей синфазности прямой (1) и головных волн (2) на сейсмограмме
На рис. 1 показана схема расположения на сейсмограмме МПВ записей прямой и головных волн при наличии в разрезе двух преломляющих границ.
Кинематические особенности волн (характер изменения времени прихода с расстоянием, наклоны осей синфазности), проявляющиеся в форме годографов, хорошо изучены (Бондарев, Крылатков, 2012). Покажем, что записи наиболее важных типов волн можно связать с определенными распределениями дифракторов в модели среды.
Прямая волна является суммой дифрагированных волн, создаваемых совокупностью дифракторов, расположенных на дневной поверхности (рис. 2, а), либо заполняющих все полупространство. Фронты этих волн от множества дифракторов на поверхности, или в среде, интерферируя, образуют фронт прямой волны (рис. 2, б).
Образование головных волн можно объяснить сложением волн, созданных дифракторами, расположенными на преломляющей границе. Могут рассматриваться несколько схем возникновения таких волн. Первая – схема с двумя дифракторами, как показано на рис. 3 а, при этом на кинематику волн влияют значения скоростей выше и ниже преломляющей границы. Вторая схема предполагает наличие одиночных дифракторов, каждый из которых располагается на преломляющей границе (рис. 4, а). Показаны сейсмограммы, рассчитанные для модели среды с параметрами: V1 = 200 м/с, V2 = 1000 м/с, глубина до границы 20 м, расстояние между дифракторами 1 м.
Во второй схеме при расчете сейсмограмм скорости распространения нисходящей и дифрагированной волны могут быть переменными, и их значения зависят от положения дифрактора по отношению к ПВ или к точке падения критической волны на преломляющую границу. Такие же подходы могут быть использованы для объяснения формирования волн других типов, присутствующих на сейсмограммах.
а б
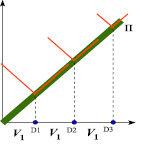
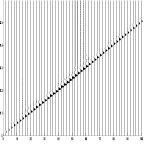
Рис. 2. Схема образования оси синфазности прямой волны (П) фронтами волн дифракторов на поверхности наблюдения (а) и расчетная сейсмограмма суммарного волнового поля таких дифракторов (б)
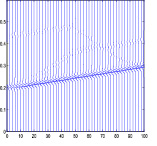
а б
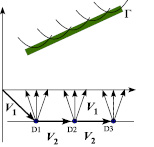
Рис. 3. Схема образования оси синфазности головной волны (Г) на основе схемы с двумя дифракторами (а) и расчетная сейсмограмма суммарного волнового поля дифракторов (б)
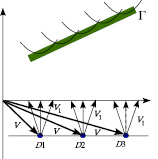
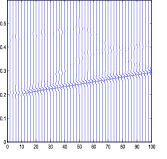
а б
Рис. 4. Схема образования оси синфазности головной волны (Г) на основе схемы с одним дифрактором на границе (а) и расчетная сейсмограмма суммарного волнового поля таких дифракторов (б)
Обобщая результаты моделирования, можно сделать вывод, что все типы волн, наблюдаемых на сейсмограммах МПВ, можно рассматривать как суперпозицию волновых полей дифракторов, связанных с сейсмическими границами или градиентными зонами.
Теоретические основы алгоритма получения сейсмических изображений по записям упругих волн на сейсмограммах
В основе способа преобразования сейсмограммы в изображение среды лежит интегральное преобразование Кирхгофа (Урупов, 2004). Использование этого интегрального преобразования позволяет на основе значений сейсмического поля на поверхности наблюдений вычислить поле во внутренних точках среды (рис. 5). Из него вытекает следующий алгоритм построения сейсмических изображений дифракторов.
Предположим, что известны координаты возможного дифрактора D(xD, zD) и значения эффективной скорости волн V на нисходящем и восходящем участках лучевой траектории, а также имеется многоканальная сейсмограмма ОТВ с трассами f(x, t). Чтобы получить элемент сейсмического изображение в одной из точек возможного нахождения дифрактора D(xD, zD), следует:
1) рассчитать траекторию оси синфазности дифрагированной волны, создаваемой этим дифрактором, для различных трасс на сейсмограмме;
2) просуммировать значения характеристик поля, взятых по этой траектории на сейсмограмме.
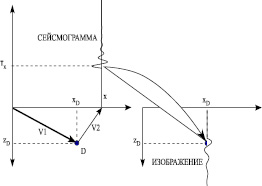
Рис. 5. Схема, поясняющая алгоритм построения сейсмического изображения среды по сейсмограмме
Таким образом, поле волн, созданных дифрактором и рассеянное по отдельным сейсмическим трассам, можно отнести к точке источника этого поля – дифрактора. Выбирая положение возможного источника-дифрактора в любой допустимой точке изображения среды, в результате многократного повторения описанной процедуры получим изображения всех источников элементарных дифрагированных волн или сейсмическое изображение изучаемой геологической среды.
Алгоритм основан на вычислении суммы амплитуд сейсмических трасс, зарегистрированных на сейсмограмме и соответствующих по времени годографу дифрагированных волн для каждой точки с координатами xD, zD. Для расчетов значений времен на годографах дифрагированных волн необходимо знание величины скоростей, соответствующих выбранной модели представления волн – скоростей инверсии.
Методика определения скоростей инверсии
В случае предположения об образовании головной волны двумя дифракторами (схема 1) в преобразовании сейсмограммы в разрез используются два значения скорости V1 и V2.
Для второй схема образования головных волн и модели среды с одной преломляющей границей на глубине h, разделяющей две среды со значениями скоростей упругих волн V1 и V2 скорость инверсии V для получения изображения среды на расстоянии x от ПВ можно найти из соотношения
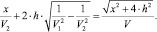
В случае использования более сложных моделей сред для определения скоростей инверсии следует применять другие расчетные формулы. Значения скоростей V1 и V2 могут быть заданы на основе общих представлений о скоростном разрезе, получены по сейсмограммам или по специальным спектрам скоростей МПВ. Для получения таких спектров нами разработан алгоритм, подобный тому, который используется для нахождения вертикальных спектров скоростей в обработке данных МОГТ. Пример изображения такого спектра скоростей показан на рис. 6. Максимумы целевой функции на этом рисунке показывают, что на сейсмограмме наблюдаются волны с соответствующими максимумам наклонами осей синфазности (значениями кажущихся скоростей).
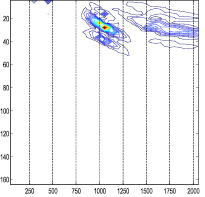
Рис. 6. Специальный спектр скоростей МПВ. По вертикальной оси показано время t0(мс). По горизонтальной – значения скоростей (м/с)
Практическая реализация алгоритмов
Алгоритм построения изображений по сейсмограммам МПВ был реализован в среде Matlab в форме скриптов. Разработаны программы, выполняющие полный цикл обработки, от чтения сейсмограмм в формате SEGY до получения сейсмического временного или глубинного разреза в этом же формате, а также программы расчета синтетических сейсмограмм и построения спектров скоростей МПВ.
Примеры опробования предлагаемых алгоритмов при обработке синтетических и экспериментальных сейсмограмм
Возможности и особенности работы предложенных нами алгоритмов были изучены на основе обработки по ним синтетических и экспериментальных сейсмограмм. Для расчетов теоретических сейсмограмм были выбраны сейсмические модели с различным числом преломляющих границ, различным их положением, наклоном и кривизной. Сейсмограммы рассчитывались на основе сверточной модели. В качестве теоретического импульса были использованы импульсы Берлаге или Риккера.
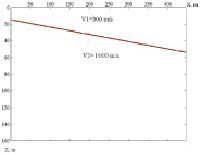
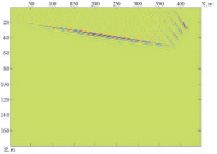
Одна из рассмотренных сейсмических моделей среды с наклонной преломляющей границей и результат преобразования серии расчетных сейсмограмм для этой модели по профилю в глубинный сейсмический разрез показан на рис. 7. Набор сейсмограмм по профилю соответствовал различным положениям на профиле пункта возбуждения. Для выполнения преобразования потребовались только ориентировочные сведения о значениях скоростей упругих волн выше и ниже преломляющей границы. Из сравнения рис. 7, а и б видно, что на итоговом разрезе четко отобразились заданные в модели параметры наклона и глубины до границы.
а б
Рис. 7. Пример получения сейсмического изображения среды по теоретическим сейсмограммам МПВ; а – модель среды; б – полученное изображение границы
а б
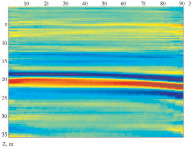
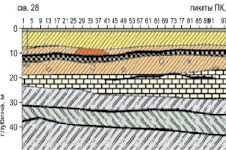
Рис. 8. Пример получения сейсмического изображения среды по экспериментальным сейсмограммам МПВ по профилю (объект д. Толочаново): а – полученное по 29 сейсмограммам суммарное сейсмическое изображение среды; б – геологический разрез по профилю
В качестве материала для проверки способа на полевых данных нами с разрешения компании «Геосигнал» использовались сейсмограммы, полученные при проведении инженерно-сейсмических исследований сотрудниками этой компании в Подмосковье, в окрестности д. Толочаново (Родыгин, Федотов, 2012.). Полевые работы выполнялись с помощью сейсмостанции ТЕЛСС-3 с 90 каналами, с шагом пунктов приема 1 м. На рис. 8 а показаны результаты обработки этих материалов по первому профилю (всего использовано 29 сейсмограмм, полученных по плотной сети наблюдений с шагом между ПВ 4 метра).
Обработка этих данных по предлагаемому нами способу дала возможность получить глубинный сейсмический разрез, который хорошо согласуется с геологическим разрезом по данным инженерно-геологического бурения (рис. 8, б).
Заключение
Исследования показали, что, используя предлагаемый алгоритм, можно выделять и несколько границ на различных глубинах. Для этого нужно использовать только различные значения скоростей. Полученные результаты показали эффективность и помехоустойчивость способа построения изображений по сейсмограммам МПВ. Его малую чувствительность к погрешностям при определении требуемых значений скоростей в изучаемом разрезе.
В результате выполненных исследований разработана теория и методика способа преобразования сейсмических данных, получаемых при работах МПВ при инженерно-геологических исследованиях, в изображения упругих характеристик геологической среды.
Рецензенты:Писецкий В.Б., д.г.-м.н., профессор, заведующий кафедрой геоинформатики, ФГБОУ ВПО «Уральский государственный горный университет», г. Екатеринбург;
Сковородников И.Г., д.г.-м.н., профессор кафедры геофизики, ФГБОУ ВПО «Уральский государственный горный университет», г. Екатеринбург.
Библиографическая ссылка
Крылатков С.М., Крылаткова Н.А., Крылевская А.Н., Гуськова В.Д. СЕЙСМИЧЕСКИЕ ИЗОБРАЖЕНИЯ ГЕОЛОГИЧЕСКОЙ СРЕДЫ В МЕТОДЕ ПРЕЛОМЛЕННЫХ ВОЛН // Фундаментальные исследования. 2015. № 2-24. С. 5409-5415;URL: https://fundamental-research.ru/ru/article/view?id=38359 (дата обращения: 05.01.2026).



