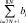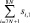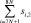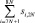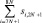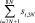Ранее, в работе [4], была выполнена постановка задачи упреждающего управления тепловыми процессами зданий при комбинированной системе отопления с использованием математической модели. В данной статье рассмотрен алгоритм решения этой задачи.
Поскольку прогноз состояния объекта управления выполняется только в пределах горизонта прогнозирования, то решение является оптимальным только для временного интервала, соответствующего данному горизонту. При этом оптимальная траектория движения системы, полученная для горизонта прогнозирования, может не совпадать с оптимальной траекторией для всего интервала, на котором осуществляется управление. Это связано с тем, что в процессе расчёта решения для текущего горизонта прогнозирования, на интервале за пределами горизонта может произойти изменение условий функционирования системы, которое не учитывается при расчётах на текущем шаге [5, 2].
На первый взгляд, квазиоптимальность является существенным недостатком упреждающего управления со скользящим горизонтом прогнозирования по сравнению с классическими методами, где обеспечивается оптимальность на всем интервале управления. Однако алгоритм упреждающего управления позволяет избежать накопления ошибки из-за долгосрочного прогноза благодаря скользящему горизонту прогнозирования и минимизировать ошибку от непрогнозируемых событий и процессов за счет пересчета управляющих воздействий на каждом шаге с учетом текущего состояния объекта управления.
Математическая модель объекта управления
В [4] была представлена уточненная математическая модель объекта управления для задачи упреждающего управления в следующем виде:
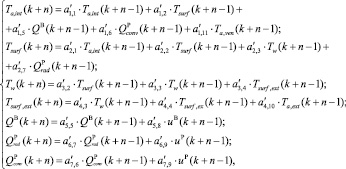(1)
и уравнение выхода в виде уравнения результирующей температуры:
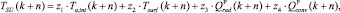(2)
где k – номер текущего шага; n – номер шага прогнозирования (n = 1…N);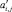 
– постоянные коэффициенты; Ta,int – температура воздуха в помещении; Tsurf – средняя температура внутренних поверхностей ограждающих конструкций; Tw – средняя температура внутреннего материала ограждающих конструкций; Tsurf,ext – средняя температура наружной поверхности ограждений; Ta,vent – температура воздуха, подаваемого в помещение приточной вентиляцией; Ta,ext – температура наружного воздуха; QB – конвективные теплопоступления от воздушного отопления; 
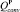– конвективные теплопоступления от радиаторного отопления; 
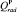– радиационные теплопоступления от радиаторного отопления; uP, uB – управляющие воздействия воздушного и радиаторного приборов отопления.
На практике чаще всего встречается релейная логика управления вентилятором воздушного отопления. В связи с этим необходимо добавить дополнительное ограничение вида
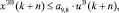(3)
где xЭВ ∈ {0, 1};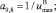 
QЭВ – электрическая мощность, потребляемая вентилятором воздушного отопления; 
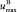– верхнее ограничение управляющего воздействия воздушного отопления.
Путем моделирования было установлено, что теплообмен между наружной поверхностью и внутренним слоем ограждения, а также между внутренним слоем и внутренней поверхностью ограждения имеет большую тепловую инерцию. Это говорит о том, что изменение температур Tw, Tsurf,ext и Ta,ext будет приводить к незначительным изменениям результирующей температуры Tsu в пределах горизонта прогнозирования и поэтому переменные состояния Tw и Tsurf,ext учитываться не будут. По этой же причине нет необходимости в прогнозировании будущих значений уличной температуры Ta,ext в пределах горизонта прогнозирования. Будем учитывать только текущее значение Ta,ext для оценки тепловых потерь. Принятые допущения упростят структуру системы управления и уменьшат размерность задачи оптимизации при незначительном снижении точности управления.
При детальном рассмотрении (1) видно, что правые части уравнений в общем случае зависят только от начальных значений переменных, полученных на шаге k, от предыдущих значений управляющих воздействий и от возмущающих воздействий. Обозначим сумму начальных значений, умноженных на соответствующие коэффициенты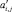 
и ai,j как bi. Коэффициенты при управляющих воздействиях будем обозначать как si,j, где i – соответствует номеру уравнения дискретной модели для горизонта прогнозирования N.
В результате вышесказанных допущений и произведенных преобразований система уравнений (1) и выражение (2) примут следующий вид:
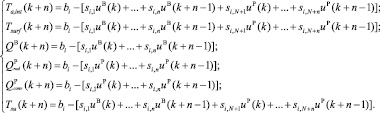(4)
Ограничения для задачи упреждающего управления из [4] и неравенство (3) после аналогичных преобразований и приведения к каноническому виду путем добавления дополнительных переменных x запишутся следующим образом:
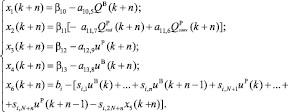(5)
Переменная x6(k + n) в последнем уравнении системы (5) является вспомогательной и добавлена для обеспечения условия неотрицательности свободных членов.
Критерий оптимальности, полученный в [4], также можно выразить через управляющие воздействия, подставив в его выражение уравнения для QB(k + n),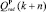 
, 
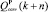из (4). Обозначим получившийся свободный член как b0, а коэффициенты при управляющих воздействиях через s0,j.
Тогда при релейном управлении вентилятором критерий оптимальности примет вид
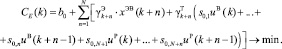(6)
Алгоритм управления
Как отмечалось в [4], для решения поставленной задачи упреждающего управления используется метод линейного программирования. Физический смысл решения задачи упреждающего управления методом линейного программирования заключается в переборе вершин области допустимых ограничений до тех пор, пока целевая функция не примет минимальное значение. Найденной вершине будут соответствовать оптимальные значения управляющих воздействий, в пределах заданного горизонта прогнозирования N и соответствующие им прогнозируемые переменные состояния [4].
В свою очередь задача линейного программирования имеет различные методы решения. Наиболее известным и распространенным является симплекс-метод. Основным преимуществом симплекс-метода является наглядность и удобство анализа процесса решения задачи благодаря представлению промежуточных результатов в виде симплекс-таблиц.
При использовании симплекс-метода переменные в левой части уравнений принято называть базисными, а дополнительная переменная x6(k + n) является искусственным базисом. Переменные в правой части уравнений называют свободными.
Для выполнения начальных условий задачи переменные, являющиеся искусственным базисом, должны быть равны нулю. Это можно обеспечить, решив вспомогательную задачу с целевой функцией вида
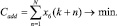(7)
Поскольку x6(k + n) ≥ 0, то оптимальному решению будет соответствовать значение целевой функции (7), равное нулю.
Решение вспомогательной задачи (4, 5, 7) позволит привести систему (5) к требуемому виду, либо, если окажется что минимум критерия (7) достигается при значении больше нуля, покажет, что система не имеет решения при заданных начальных условиях.
Второй вариант возможен, если система управления не может перевести объект из исходного состояния в конечное, которое удовлетворяет заданным ограничениям за время, соответствующее горизонту прогнозирования. Такая ситуация может случиться при включении системы и ее выходе на заданный график работы. Данную проблему можно решить, используя граничные значения управляющих воздействий uP и uB, в зависимости от знака разницы заданного и реального значения результирующей температуры:
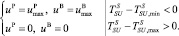(8)
Учитывая, что выход системы за область допустимых решений случается довольно редко, при возникновении внештатных ситуаций, то использование последнего описанного способа для подобных ситуаций не окажет большого влияния на увеличение стоимостных затрат на потребляемую системой отопления энергию в целом.
Симплекс-метод предполагает построение симплекс-таблиц, состоящих из свободных членов и коэффициентов систем (4, 5) и целевой функции (6).
Ниже приведем алгоритм решения задачи с использованием симплекс-таблиц [3].
1. Заполняется симплекс-таблица для вспомогательной задачи (таблица).
Каждая строка таблицы соответствует уравнению из системы (4) и (5), а последняя строка соответствует целевой функции.
2. В строке коэффициентов целевой функции (не считая свободного члена) выбирается отрицательное значение коэффициента, обычно максимального по модулю. Если все коэффициенты положительны и свободный член в строке Cadd равен нулю, то оптимальное решение достигнуто, причем значения переменных определяются столбцом свободных членов, а оптимальное значение функции – клеткой, соответствующей свободному члену.
3. В столбце j = j0, который соответствует выбранному на предыдущем шаге коэффициенту целевой функции, среди положительных коэффициентов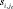 
выбирается разрешающий элемент 
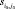, т.е. элемент для которого минимально отношение 
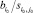. Если положительных коэффициентов нет, то задача не имеет решения.
4. Все члены строки, содержащей разрешающий элемент, делятся на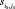 
. Полученная строка вносится на то же место в новой таблице.
5. Из каждой оставшейся i-й (i ≠ i0) строки вычитается получившаяся строка, умноженная на коэффициент 
оставшейся строки. В результате в клетках, соответствующих столбцу j = j0, появляются нули. Преобразованные строки записываются в новой таблице на место прежних. Вместо базисной переменной с индексом i0 записывается свободная переменная с индексом j0. Свободная переменная при этом не заменяется.
Далее идет переход на шаг 2.
После того, как оптимальное решение достигнуто (свободный член в строке целевой функции равен нулю), переходим к решению основной задачи.
Начальная симплекс-таблица исходной задачи будет соответствовать последней таблице вспомогательной задачи (в которой свободный член в строке целевой функции равен нулю), за исключением строки, содержащей целевую функцию. Если в целевой функции (6) присутствуют переменные, которые после решения основной задачи стали базисными, то эти переменные необходимо выразить через свободные путем подстановки.
Пример симплекс-таблицы
|
Базис |
Свободные переменные |
|||||||
|
uB(k) |
uB(k + 1) |
… |
uP(k + N) |
x5(k) |
… |
x5(k + N) |
||
|
Ta,int(k + 1) |
b1 |
s1,1 |
s1,2 |
… |
s1,2N |
0 |
… |
0 |
|
Ta,int(k + 2) |
b2 |
s2,1 |
s2,2 |
… |
s2,2N |
0 |
… |
0 |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
x6(k + n) |
b8,N |
s8N,1 |
s8N,2 |
… |
s8N,2N |
–s8N,2N+1 |
… |
–s8N,3N |
|
–Cadd |
|
|
|
… |
|
|
… |
|
Алгоритм решения основной задачи аналогичен вышеописанному, за исключением того, что оптимальное решение определяется на шаге 2 только путем отсутствия отрицательных коэффициентов в строке, соответствующей целевой функции.
Поскольку управление воздушным вентилятором происходит релейно, то после решения основной задачи необходимо еще решить частично целочисленную задачу. Для этого воспользуемся методом отсечения (Гомори), который схож с симплекс-методом [3].
Суть метода Гомори заключается в построении дополнительных ограничений, которые определенным образом уменьшают исходную область допустимых решений, пока все требуемые переменные не примут целые значения.
Алгоритм, используемый при решении частично целочисленной задачи линейного программирования, имеет следующую последовательность:
1. Найти оптимальное решение задачи (4–6) без условия целочисленности. Если xЭВ(k + n) ∈ {0, 1}, для n = 1…N, то задача решена, в противном случае перейти к шагу 2.
2. Выбрать среди xЭВ(k + n), при n = 1…N дробную переменную с максимальной дробной частью и построить дополнительное ограничение по соответствующей ей i-й строке [1]:
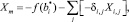(9)
где X – переменная состояния; m – новая строка в симплекс-таблице.
Значение коэффициента δi,j определяется исходя из следующих условий.
a) для переменных состояния, которые могут принимать нецелочисленные значения:
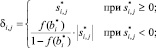(10)
б) для переменных состояния, принимающих только целочисленные значения:
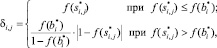(11)
где 
и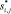 
– модифицированный свободный член и коэффициенты переменных состояния соответственно, полученные в результате решения задачи на шаге 1; 
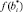и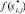 
– дробные части чисел 
и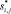 
(где дробная часть это такое наименьшее неотрицательное число, что разность между исходным и этим числом есть целое).
3. Добавить дополнительное ограничение (9) к последней полученной симплекс-таблице и перейти к шагу 1.
Вышеописанный алгоритм выполняется на каждом шаге k. Результатом решения являются значения управляющих воздействий радиаторного и воздушного отопления для каждого шага в пределах заданного горизонта N. Реализуются управляющие воздействия только для текущего шага, затем осуществляется переход на следующий шаг и расчеты повторяются.
На рисунке приведен график изменения результирующей температуры Tsu и прогноза результирующей температуры Tsu,p, полученный в результате моделирования работы алгоритма упреждающего управления для прерывистого режима.
Моделирование проводилось при следующих условиях:
– тепловая мощность воздушного и радиаторного отопления по 4 кВт;
– объем помещения: 300 м3;
– время начала и окончания рабочего режима соответствует 3,5 и 15,5 ч;
– горизонт прогнозирования: 5 шагов при величине шага прогнозирования 800 секунд;
– температура уличного воздуха изменяется по синусоидальному закону с периодом 24 ч, амплитудой 10 °С относительно –5 °С.
Значения прогноза результирующей температуры приведены для последнего (пятого) шага горизонта прогнозирования, прогноз которого является наименее точным. Полученные графики демонстрируют работоспособность представленного алгоритма и достаточно высокую точность прогнозирования. Преимуществом рассмотренного алгоритма является то, что он не требует сложных аналитических выводов и использует стандартные подходы для расчёта стратегии управления, что упрощает его практическую реализацию по сравнению с классическими алгоритмами оптимизации.
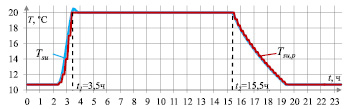
Графики изменения и прогноза результирующей температуры
Рецензенты:
Панферов В.И., д.т.н., профессор, заведующий кафедрой «Теплогазоснабжение и вентиляция», ФГБОУ ВПО «Южно-Уральский государственный университет», г. Челябинск;
Казаринов Л.С., д.т.н., профессор, декан факультета «Компьютерные технологии, управление и радиоэлектроника», ФГБОУ ВПО «Южно-Уральский государственный университет», г. Челябинск.
Библиографическая ссылка
Румянцев Д.В., Тверской М.М. АЛГОРИТМ УПРЕЖДАЮЩЕГО УПРАВЛЕНИЯ ТЕПЛОВЫМИ ПРОЦЕССАМИ ЗДАНИЯ ПРИ КОМБИНИРОВАННОЙ СИСТЕМЕ ОТОПЛЕНИЯ // Фундаментальные исследования. – 2015. – № 2-24. – С. 5371-5376;URL: https://fundamental-research.ru/ru/article/view?id=38352 (дата обращения: 24.11.2024).