Для проведения эффективного прогноза нефтегазоносности необходимо построение объемной структурно-плотностной модели геологической среды, удовлетворяющей гравитационному полю. Однако для построения имеются только фрагментарно заданные данные, в том числе профильные. Построенные двумерные модели могут быть реконструированы решением структурной или плотностной обратных задач гравиразведки [1–5]. Для преобразования двумерных данных в трехмерные существует много прикладных программных средств (например, Surfer, Коскад 3D и др.), алгоритмов (послойной интерполяции, методы крайгинга и др.), выбор которых зависит от характера имеющихся данных. В данной работе представлена разработка алгоритмов и вычислительных схем интерполяции профильных данных в объемные плотностные модели, основные положения которых изложены в [6, 7].
Исходные данные в условиях недоопределенности задаются системой профилей Γ, Γ = {Γl}, l = 1, ..., P, в которую входит P геолого-геофизических разрезов. Систему координат рассматриваем с осью Oz, направленной вниз и плоскостью xOy – совмещённой с дневной поверхностью. Для всех разрезов также имеются координаты начала и конца в новой, общей системе координат. Для представления структурной модели по каждому профилю каждой точке x сопоставляется глубина залегания z = fk(x) соответствующей границы k = 0, 1, ..., N, лежащей в области S, ограниченной горизонтальной полосой П. Каждый из пластов характеризуется своим неизменным по вертикали параметром плотности σk(x).
Необходимо по имеющимся данным построить объемную структурно-плотностную модель среды [1, 2, 3]. В ней каждой точке s = {x, y} пространства V, ограниченного горизонтальной полосой П, сопоставляется глубина залегания z = fk(s) соответствующей границы k = 0, 1, ..., N. Каждый из пластов характеризуется своим параметром плотности σk(s), неизменным по вертикали в пределах каждого из пластов (рис. 1). В этом случае модель представляет собой следующее:
– границы, ограничивающие пласты, представляют собой однозначные функции пространственных координат zk = fk(s), k = 0, 1, ..., N + 1;
– плотность пласта, заключенного между k-й и k + 1-й границами, есть функция горизонтальных координат σk +1 = σk +1(s), k = 0, 1, ..., N;
– нулевая граница есть горизонтальная пластина с глубиной f0 и плотностью пласта σ0;
– плотность среды ниже границы с номером N есть σN+1;
– величины f0, σN+1, σ0 считаются постоянными;
– объемная модель 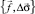 имеет след на поверхности {l} – проходящей через линию Г1 нормально к дневной поверхности двухмерную модель
имеет след на поверхности {l} – проходящей через линию Г1 нормально к дневной поверхности двухмерную модель 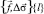 .
.
Для объемной структурной модели введем краткое обозначение:
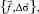
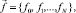
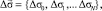
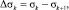
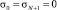 .
.
Здесь Δσk – контрастность k-го пласта.
Для построения объемной структурно-плотностной модели по системе профилей разработаны следующие алгоритмы интерполяции Q(Γ): односторонняя линейная интерполяция, «змейка», рекурсия (прямоугольная). Алгоритм интерполяции системы 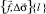 , заданной на профилях Γ в объемную модель
, заданной на профилях Γ в объемную модель 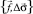 обозначим Q(Γ):
обозначим Q(Γ):
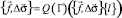 .
.
Каждый алгоритм состоит из двух этапов:
Аппроксимация по профилям. По каждому профилю Гl находим значения глубин 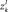 и плотностей
и плотностей 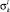 с заданным разбиением step_r. Координаты по горизонтали для каждой из границ
с заданным разбиением step_r. Координаты по горизонтали для каждой из границ 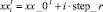 , где k = 0, ..., N – номера границ, l = 1, ..., P – номера профилей, i = 0, ..., Pl – число точек, получившихся при интерполяции на соответствующем профиле и xx_0l – координаты начала профилей. Для приведения данных к системе координат производим поворот осей на угол αl, образованный соответствующим профилем с осью Ox. Здесь значения x_dl – координаты начала l-го профиля в новой системе координат
, где k = 0, ..., N – номера границ, l = 1, ..., P – номера профилей, i = 0, ..., Pl – число точек, получившихся при интерполяции на соответствующем профиле и xx_0l – координаты начала профилей. Для приведения данных к системе координат производим поворот осей на угол αl, образованный соответствующим профилем с осью Ox. Здесь значения x_dl – координаты начала l-го профиля в новой системе координат 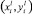 :
:
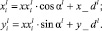 (1)
(1)
Аппроксимация по площади. С целью оптимизации математических расчетов в качестве объекта выбирается прямая призма, представляющая собой совокупность структурно-плотностных разрезов по профилям. Для получения по рассматриваемой площади 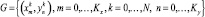 значений глубин залегания fk(G) и плотностей σk(G) разбиения используем линейную интерполяцию данных по профилям. Размеры ячейки сетки Δx и Δy по осям Ox и Oy. Координаты призмы по осям меняются: от
значений глубин залегания fk(G) и плотностей σk(G) разбиения используем линейную интерполяцию данных по профилям. Размеры ячейки сетки Δx и Δy по осям Ox и Oy. Координаты призмы по осям меняются: от  до
до 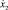 по оси Ox, от
по оси Ox, от 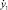 до
до 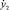 >по оси Oy и от
>по оси Oy и от  до
до  >по оси Oz (рис. 2).
>по оси Oz (рис. 2).
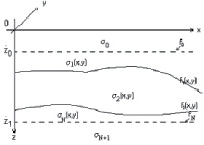
Рис. 1. Объемная структурно-плотностная модель среды
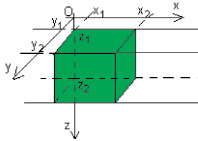
Рис. 2. Тестируемая модель
В основе интерполяции лежит метод сравнения трех ближайших к рассматриваемой 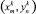 точек с известными глубинами и плотностями с последующей интерполяцией на сетку. Для каждой из границ последовательность действий одинакова, поэтому индекс k опустим.
точек с известными глубинами и плотностями с последующей интерполяцией на сетку. Для каждой из границ последовательность действий одинакова, поэтому индекс k опустим.
Односторонняя интерполяция. Обход полученной сетки G для каждой границы производим слева направо. Последовательность действий представляет собой итерационную процедуру, которую опишем для произвольной точки (xm, yn).
Шаг 1. Находим точку 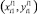 на l профиле, имеющую минимальное расстояние до исследуемой:
на l профиле, имеющую минимальное расстояние до исследуемой:
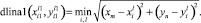
Здесь 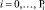 – номер точки. Это точка вида 1. Если расстояние меньше половины диагонали ячейки построенной сетки, то
– номер точки. Это точка вида 1. Если расстояние меньше половины диагонали ячейки построенной сетки, то
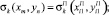
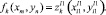
Шаг 2. Ищем по профилям ближайшую к исследуемой точку 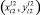 , лежащую справа от (xm, yn) в полосе
, лежащую справа от (xm, yn) в полосе
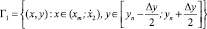
и находящейся от нее на расстоянии
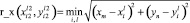
(точка вида 2).
Шаг 3. Далее находим ближайшую по профилям к исследуемой точку 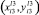 , лежащую в полосе
, лежащую в полосе
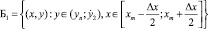
(точка вида 3) и находящейся от нее на расстоянии
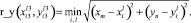
Схематично описанные выше виды точек интерполяции приведены на рис. 3.
Шаг 4. В случае граничных точек сетки используются особые способы нахождения значений глубин и плотностей:
1. В точках нижней границы сетки (n = 0) значениям глубин и плотностей модели присваиваем значения, принадлежащие точке первого вида 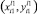 .
.
2. В точках левой границы сетки (m = 0) искомым величинам присваиваем среднее значение соседних нижних (x0, yn–1) и (x1, yn–1) точек:
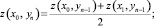
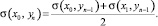 (2)
(2)
3. В точках правой (m = Kx) и верхней (n = Ky) границ сетки искомым характеристикам присваиваем среднее значение соответствующих характеристик предыдущей (xm–1, yn) и нижней (xm, yn–1) точек:
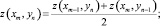
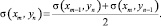 (3)
(3)
Шаг 5. После нахождения точек приступаем к сравнению расстояний от них до исследуемой точки:
1. Если нет точек вида 2 и вида 3, то используем формулы (3).
2. Если r_x ≥ r_y или нет точек 2 вида, то составляем уравнение прямой, проходящей через точки 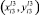 и (xm, yn–1). В результате получаем
и (xm, yn–1). В результате получаем
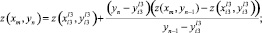
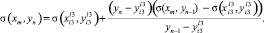 (4)
(4)
3. Если r_x < r_y или нет точек вида 3, то составляем уравнение прямой, проходящей через точки 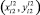 и (xm–1, yn) (левую и вида 2):
и (xm–1, yn) (левую и вида 2):
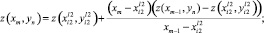
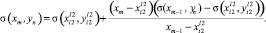 (5)
(5)
Шаг 6. Выбрав удовлетворяющие имеющимся данным уравнения, находим интересующие нас величины для точки (xm, yn) и переходим к шагу 1, где находим плотность и глубину залегания точки z(xm+1, yn) или z(x0, yn+1), если m = Kx.
«Змейка». Данная интерполяция отличается от предыдущей направлением обхода узлов сетки G, т.е. порядком заполнения данных точек (xm, yn).
1. В четном горизонтальном ряду (n = 0, 2, ...) движемся слева направо и заполняем узлы сетки, как в предыдущей интерполяции.
2. В нечетном горизонтальном ряду (n = 1, 3, ...) движемся справа налево.
Существуют следующие отличия от алгоритма предыдущей интерполяции:
Шаг 2. Вместо точки вида 2 находим точку вида 4 в полосе слева:
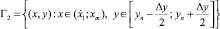
и находящейся от нее на расстоянии
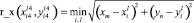 .
.
Вместо (5) составляем уравнение прямой, проходящей через точки 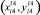 и (xm+1, yn):
и (xm+1, yn):
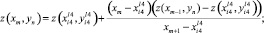
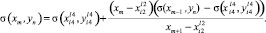 (6)
(6)
Шаг 4
1. В граничных точках слева (m = 0) искомым величинам присваиваем среднее значение правой (x1, yn) и нижней (x0, yn–1) точек:
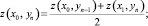
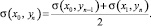 (7)
(7)
2. В граничных точках справа (m = Kx) глубины и плотности находим следующим образом: берем среднее значение нижней 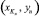 и нижней предыдущей
и нижней предыдущей 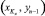 :
:
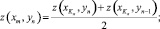
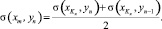 (8)
(8)
Шаг 5.
1. Если нет точек вида 4 и 3, то искомым характеристикам присваиваем среднее правого (xm+1, yn) и нижнего (xm, yn–1) значений в найденных ранее узлах
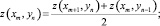
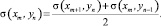 (9)
(9)
Прямоугольная (Рекурсия). Обход начинается с центра сетки и продолжается против часовой стрелки вокруг этой центральной точки. Возможны 4 варианта нулевого элемента (рис. 4):
а) одна точка;
б) вертикальный ряд точек;
в) горизонтальный ряд точек;
г) набор точек, образующий квадрат.
Рассмотрим порядок действий алгоритма для каждого элемента.
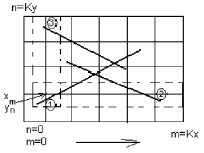
Рис. 3. Виды точек сетки односторонней интерполяции
а) Ищем точку вида 1 и искомым значениям присваиваем ее характеристики.
б) Двигаемся снизу вверх. Первую точку заполняем, как в (а). Для остальных точек добавляем сравнение с ближайшей точкой в вертикальной полосе сверху, с мощностью Δy (точка вида 3).
в) Двигаемся слева направо. Первую точку заполняем, как в (а). В остальных добавляем сравнение с ближайшей точкой в горизонтальной полосе справа, с мощностью Δx (точка вида 2).
г) Движение производим по кругу. Первую точку заполняем, как в (а). Вторую, как в (в). Третью, как в (б). При работе с последней точкой добавляем сравнение с ближайшей точкой в вертикальной полосе сверху, с мощностью Δy (точка вида 3) и с ближайшей в горизонтальной полосе слева, с мощностью Δx (точка вида 4).
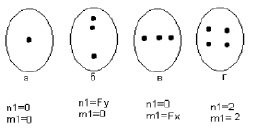
Рис. 4. Виды точек, характерных для интерполяции «рекурсия»
Таким образом, выше полностью описан алгоритм Q(Γ) интегрирования профильных данных в объемную модель 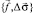 , разработанный для крупных плотностных структур типа седиментационных бассейнов. В настоящее время ведется проверка алгоритмов на устойчивость, выработка рекомендаций по выбору шага и типа интерполяции.
, разработанный для крупных плотностных структур типа седиментационных бассейнов. В настоящее время ведется проверка алгоритмов на устойчивость, выработка рекомендаций по выбору шага и типа интерполяции.
Рецензенты:
Бурмистрова О.Н., д.т.н., заведующий кафедрой технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Андронов И.Н., д.т.н., профессор, заведующий кафедрой сопротивления материалов и деталей машин, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Библиографическая ссылка
Кобрунов А.И., Мотрюк Е.Н., Ломинский Д.О. МЕТОД ИНТЕРПОЛЯЦИИ ГЕОЛОГИЧЕСКОЙ СРЕДЫ В УСЛОВИЯХ ФРАГМЕНТАРНО ЗАДАННЫХ ДАННЫХ // Фундаментальные исследования. 2015. № 2-24. С. 5340-5345;URL: https://fundamental-research.ru/ru/article/view?id=38346 (дата обращения: 12.02.2026).



