В современном мире защита информации от несанкционированного доступа и подмены имеет огромное значение, особенно защита изображений и видеопотоков в сетях общего пользования [10, 13, 16]. Большинство традиционных систем, успешно применяемых на практике, не могут впрямую использоваться для защиты цифрового видео в системах реального времени, поскольку базируются на алгоритмах шифрации и требуют значительных вычислительных затрат. В то же время известны [15] матричные методы кодирования видеоинформации, которые могут быть использованы в том числе для защиты видеокадров от несанкционированного просмотра.
Для указанной цели в работах [13, 14] были предложены относительно простые и реализуемые в реальном времени процедуры маскирования изображений, основанные на матричных преобразованиях кадров видеопотока.
Теория маскирования и исследование свойств маскированных изображений в последнее время значительно интенсифицировались [12, 14], однако однозначного ответа на вопрос о выборе вида матриц (матричных базисов) на сегодня не существует.
В настоящей работе анализируются преимущества и недостатки матричных базисов, которые можно использовать для задач маскирования.
Основные определения
Определение 1. Маскирование – вычислительная процедура преобразования цифрового изображения, разрушающая его до вида, воспринимаемого визуально как шум.
Задачей маскирования является сохранение изображения в недоступном третьей стороне виде в течение времени актуальности этого изображения.
В настоящей работе ограничимся системами передачи видео по сетям общего пользования, время актуальности для которых определяется в минутах или десятках минут. Это как коммерческие сетевые системы трансляции, так и специальные системы видеонаблюдения за распределенными объектами, видеомониторинга территорий и массовых мероприятий и др.
Определение 2. Маскирование видеопоследовательности – вычислительная процедура преобразования цифровых изображений кадров, разрушающая их до вида, не позволяющего визуально различать объекты съемки и целостно воспринимать по последовательности кадров сценарий событий.
Определение 3. Матричное маскирование – вычислительная процедура преобразования цифровых изображений с использованием матричных операций, разрушающая его до вида, воспринимаемого визуально как шум.
Определение 4. Матричное демаскирование – вычислительная процедура обратного преобразования с использованием матричных операций, восстанавливающая исходное цифровое изображение из маскированного.
Задача организации процесса матричного маскирования/демаскирования изображений (отдельных кадров видеопотока) состоит в простоте и симметричности выполняемых преобразований изображений в системе передачи по открытым сетям.
Очевидно, что при симметричности системы прямое преобразование матрицей требует в обратном преобразовании матрицы, обратной к маскирующей.
В общем случае как исходная, так и обратная матрицы порядка n могут иметь до n2 уровней – по числу элементов матриц.
Рассмотрим три способа получения обратной матрицы по исходной.
В общем случае для матрицы An порядка n существует обратная матрица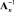 
такая, что
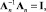
где I = diag(1, 1, 1, …, 1). Однако процедуры вычисления обратной матрицы предполагают выполнение операций умножения и деления общим количеством не менее чем О(n3). Это первый способ получения обратной матрицы, не позволяющий вычислить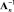 
точно. Выполнимо лишь 
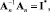, где I – I*≠ 0. Кроме того, плохая определенность исходной матрицы ставит под сомнение саму возможность вычисления обратной [11].
Определение 5. Жакетной матрицей называется матрица Ln c элементами lij, для которой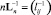 
[20–21].
Очевидно, для таких матриц вычисление обратной матрицы заменяется инверсией элементов исходной – это второй способ, менее трудоемкий. Однако даже на порядках матриц Адамара не для всех значений n жакетные матрицы существуют, что является сдерживающим фактором для широкого их применения в маскировании.
В предположении, что современные видеокадры имеют различные размеры в цифровом выражении – от стандартов прошлого века PAL, SECAM, NTSC до современных HD, Full HD, 4K и т.д., а также реализуются режимы передачи видеоизображений с выделением произвольного окна качества (Quality Box) – в арсенале маскиратора/демаскиратора должны быть матрицы различных порядков. Идеальным является вариант, когда порядки матриц из множества в базисе соответствуют множеству всех натуральных чисел.
Для ортогональных и квази-ортогональных матриц, к которым относятся матрицы Адамара, матрицы Адамара – Мерсенна [7], Адамара – Эйлера [6], Мерсенна – Уолша [1] и базисов на их основе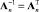 
. Это третий и наиболее простой способ получения обратных матриц, не требующий вычислительных затрат.
Определение 6. Уровнями матрицы [3, 5] называются численные значения, которым равны ее элементы.
Кроме матриц Адамара – квадратных двухуровневых матриц Hn порядка n, состоящих из чисел {1, –1}, столбцы которых ортогональны
,
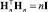где I = diag(1, 1, 1, …, 1), существуют матрицы квази-ортогональные – локально-оптимальные по адамаровой норме [18].
Из рассмотренного выше следуют основные вопросы – насколько просто получение исходных ортогональных и квази-ортогональных матриц, имеющих обратные в виде транспонированных? Сколько матриц в базисе двухуровневых матриц?
Определение 7. Матрица Адамара – Мерсенна [7] – двухуровневая матрица Mn порядка n, состоящая из элементов {a = 1, –b}, столбцы которой х ортогональны
,
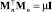где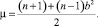 
Значение уровня –b определяется при n > 3 как 
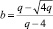, q = n + 1 – порядок матрицы Адамара.
Матрицы Адамара – Мерсенна дополняют множество матриц Адамара на классе ортогональных матриц и существуют на нечетных порядках n = 2k – 1 (k – целое), равных числам последовательности Мерсенна. Однако, согласно гипотезе [23], множества матриц Адамара и Адамара – Мерсенна являются равновеликими и матрицы Адамара – Мерсенна существуют на всех порядках 4k – 1.
Число квази-ортогональных матриц Адамара – Мерсенна не уступает числу целочисленных матриц Адамара, но значения коэффициентов двухуровневых матриц Адамара – Мерсенна – вещественные числа, что позволяет лучше защитить видеоинформацию.
Цепочки квази-ортогональных матриц
С матрицами Адамара – Мерсенна тесно связано множество матриц Адамара – Эйлера [6], существующих на порядках 4k - 2.
Последовательность матриц Адамара – Мерсенна хотя и начинается с тривиальной матрицы первого порядка, однако базовой можно считать матрицу третьего порядка [7] вида
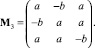
Для итерационного получения ортогональных двухуровневых матриц Адамара – Мерсенна последующих порядков из предыдущих на основе формулы Сильвестра строятся сначала четырехуровневые матрицы Адамара – Эйлера
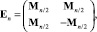
где Mn/2 – двухуровневая матрица Адамара – Мерсенна вдвое меньшего нечетного порядка [6]. При этом преобразовании число уровней удваивается ввиду инверсии двухуровневой матрицы Адамара – Мерсенна.
Следующий шаг заключается в пересчете матрицы Адамара – Эйлера в матрицу Адамара – Мерсенна дополнением ее строкой и столбцом (каймой) в виде [6]:
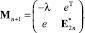
Здесь λ = –a – собственное число, а e – собственный вектор «сопряженной» матрицы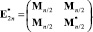 
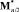получатся из матрицы Мерсенна соответствующего порядка взаимной заменой элементов a = 1 и –b, причем первую половину отличных от a коэффициентов собственного вектора составляют элементы –b. При n > 3 уровень 
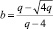, q = n + 1 (порядок матрицы Адамара).
Из приведенных выше формул видно, что такая последовательность действий позволяет снова вернуться к двухуровневому варианту матрицы Адамара – Мерсенна, порядок которой соответствует следующему числу в последовательности Мерсенна.
Матрицы Эйлера модульно двухуровневые [6], дополняющие базис квази-ортогональных матриц, они также могут использоваться в процедурах маскирования.
Приведенная последовательность действий описывает процедуру вычисления цепочек матриц как механизм существенного расширения квази-ортогонального базиса для задач маскирования.
Обращает на себя внимание тот факт, что на дополнительных порядках n = 10∙2k (n = 10, 20, 40, 80, 160, 320, 640 и т.д.) существуют квази-ортогональные G-матрицы [20, 21], связанные с матрицами Адамара – Эйлера и занимающие особое место в алгоритмах обработки изображений.
Особенности алгоритмов маскирования на цепочках матриц
Типичный тракт обработки изображения в процедуре матричного маскирования рассмотрен в работах [17, 24]. Особенность использования в ней рассмотренных квази-ортогональных базисов заключается в том, что, во-первых, порядки входящих в них матриц закрывают значительную часть множества натуральных чисел, включая кратные традиционным размерам изображений.
Во-вторых, кроме дискретности уровней элементов матрицы, как у матрицы Адамара, не менее важную роль при преобразовании играет оригинальность базиса, обеспечивающая скрытность получаемых маскированных данных. Это делает двухуровневые матрицы с иррациональными значениями уровней удобными при выполнении процедуры маскирования изображений на цифровых устройствах.
В-третьих, в отличие от традиционных базисов в задаче маскирования большое значение имеют дополнительные качества, обретаемые из экстремальных свойств базисных наборов. Матрицы Адамара и близкие к ним матрицы Мерсенна оптимальны в смысле нейтрализации последствий воздействия точечных помех при передаче по коммуникационным каналам.
В-четвертых, не менее важны рекурсивные процедуры увеличения порядка матрицы. Дополнительный аргумент рациональности использования базисов, построенных на последовательностях чисел, состоит в том, что алгоритм построения их фрактален и матрицы при определенном устройстве алгоритма обладают повышенной чувствительностью к изменению разрядной сетки процессора и начальных данных.
Современное состояние процессоров цифровой обработки сигналов, характеризующееся увеличением производительности и структурной ориентацией на выполнение операции свертки в формате вещественных чисел, позволяет эффективно использовать описанные и более сложные базисы – многоуровневые М-матрицы [5].
Заключение
В процессе поиска для алгоритмов маскирования изображений оригинальных ортогональных матриц нечетных порядков, близких к матрицам Адамара по свойствам, выделен предпочтительный класс двухуровневых матриц Адамара – Мерсенна. Порядки этих матриц равны числам Мерсенна вида 2k – 1, однако их состав значительно расширяется гипотезой Балонина до 4k – 1.
Инструмент для поиска новых матриц Адамара – Мерсенна с отличными от рассмотренных матриц структурами существует в виде программного комплекса [9, 19]. Комплекс может быть использован при усложнении задачи маскирования видеоизображений, заключающемся в том, что матрица ортогонального преобразования не вычисляется заранее, а является результатом работы алгоритма. По открытому каналу в качестве ключа передаются только настройки для ее вычисления.
Практическое применение рассмотренных в работе базисов матриц целесообразно в задачах повышения степени помехоустойчивости и защищенности при передаче информации по открытым каналам коммуникаций.
Рецензенты:Шалыто А.А., д.т.н., профессор, зав. кафедрой «Технологии программирования», ФГАОУ ВО «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики», г. Санкт-Петербург;
Юлдашев З.М., д.т.н., профессор, зав. кафедрой биотехнических систем, «Санкт-Петербургский государственный электротехнический университет им. В.И. Ульянова (Ленина)», г. Санкт-Петербург.
Библиографическая ссылка
Востриков А.А., Мишура О.В., Сергеев А.М., Чернышев С.А. О ВЫБОРЕ МАТРИЦ ДЛЯ ПРОЦЕДУР МАСКИРОВАНИЯ И ДЕМАСКИРОВАНИЯ ИЗОБРАЖЕНИЙ // Фундаментальные исследования. – 2015. – № 2-24. – С. 5335-5339;URL: https://fundamental-research.ru/ru/article/view?id=38345 (дата обращения: 24.11.2024).