Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лагунов Н.А. 1

---

1 Северо-Кавказский федеральный университет

Настоящая статья посвящена проблеме выделения и распознавания объектов. Приводятся улучшения, которые возможно применить к одной из наиболее перспективных и новых моделей R-CNN. Большинство современных наиболее эффективных моделей не приспособлены для работы в реальном времени, что является большим препятствием для развития робототехнических систем. Основное внимание в статье уделено повышению скорости работы алгоритма, а также использованию сверточных нейронных сетей высокого порядка. Описываются изменения в алгоритме селективного поиска для уменьшения количества генерируемых гипотез, приводятся результаты экспериментов по внедрению нейронов высоких порядков в нейронную сеть, изложен способ ускорения сверточных нейронных сетей с помощью векторно-матричных процессоров. Таким образом, в статье содержится информация о том, как возможно улучшить модель R-CNN, ускорив ее работу и не потеряв при этом в качестве выделения и распознавания объектов.

Статья в формате PDF

369 KB

нейронные сети

распознавание

выделение объектов

нейроны высоких порядков

векторно-матричные процессоры

ускорение

1. Лагунов Н.А. Исследование применимости процессоров с векторно-матричной архитектурой для реализации нейронных сетей // Параллельная компьютерная алгебра и ее приложения в новых инфокоммуникационных системах: материалы I международной конференции. – 2014.

2. Царегородцев В.Г. Сверточные нейронные сети с полиномиальными (high-order) сумматорами нейронов [Электронный ресурс]. – URL: neuropro.ru/memo334.shtml (дата обращения: 17.01.2015).

3. BING: Binarized Normed Gradients for Objectness Estimation at 300fps. Ming-Ming Cheng, Ziming Zhang, Wen-Yan Lin, Philip Torr, IEEE CVPR, 2014.

4. Dina Dushnik Video Segmentation via Diffusion Bases / D. Dushnik, A. Schclar, A. Averbuch – School of Computer Science, Israel, 2013.

5. Ross Girshick Rich feature hierarchies for accurate object detection and semantic segmentation / R. Girshick, J. Donahue, T. Darell, J. Malik – IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014.

Система детектирования объектов R-CNN впервые была представлена в 2014 году в [5] и состоит из трех модулей. Первый модуль генерирует гипотезы о местоположении объекта на изображении независимо от класса объекта. Второй модуль представляет из себя большую сверточную нейронную сеть, которая извлекает признаки из каждой гипотезы, преобразуя их в вектор фиксированной длины. Третий модуль – это машина опорных векторов, осуществляющая классификацию векторов признаков на наборе конкретных классов объектов.

Модель имеет хорошие показатели качества выделения объектов, но рассчитана на работу со статичными изображениями и имеет среднее время работы 15 секунд, что не позволяет использовать ее в реальном времени. Улучшения, предлагаемые в данной работе, можно разделить на следующие пункты:

1. Оптимизация алгоритма селективного поиска с целью существенного снижения количества генерируемых гипотез, а следовательно, времени их обработки.

2. Использование сверточной нейронной сети высокого порядка для улучшения качества распознавания объектов.

3. Ускорение сверточной нейронной сети с использованием векторно-матричных процессоров, для компенсации повышения алгоритмической сложности сети.

Цель исследования – адаптировать модель выделения объектов R-CNN для работы в режиме реального времени без существенных потерь в качестве распознавания.

Материал и методы исследования – моделирование, эмпирический эксперимент, измерение и анализ результатов.

Селективный поиск на сегодняшний день является одним из самых совершенных и точных алгоритмов нахождения алгоритмов на изображении и включает множество разнообразных стратегий для рассмотрения изображения с как можно более обширного числа точек зрения.

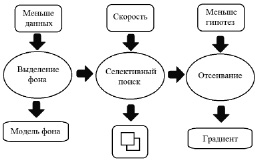
Рис. 1. Модель оптимизации алгоритма селективного поиска

Главная идея заключается в том, чтобы ускорить выделение объектов с помощью селективного поиска путем уменьшения количества генерируемых гипотез. Сделать это возможно за счет понижения размерности обрабатываемых данных путем фильтрации исходного изображения на основе его изменений во времени, а также исключения гипотез, для которых можно сделать вывод, что они не относятся ни к одному из целевых объектов, на основании размера, содержания и распределения цветов на изображении. Схема приведена на рис. 1.

Таким образом, улучшения модели выделения объектов на изображении можно разделить на три группы:

1. Предварительное выделение фона от «новых» областей на изображении. Этот этап приводит к значительному уменьшению количества обрабатываемых данных и времени, затрачиваемого на генерацию гипотез.

2. Изменения в модели селективного поиска:

– исключение использования больших масштабов при иерархической обработке изображения;

– отбрасывание слишком больших и слишком малых гипотез, которые в любом случае не будут покрывать зоны, в которых может появиться объект;

– исключение объектов, имеющих тонкую, длинную структуру (менее 30 % пикселей от общей площади, занимаемой фигурой).

3. Дополнительное отсеивание окон-кандидатов на основе цветового профиля и низкоуровневой структуры.

В табл. 1 представлены результаты для различных алгоритмов выделения фона на основе 1 – Медианного фильтра, 2 – Гауссова среднего, 3 – Применения ядер свертки, 4 – Изменения собственных векторов сегментов изображения, 5 – Изменения собственного вектора всего изображения [4].

Следовательно, наибольшую точность выделения фона дал метод использования ядер и операции свертки, но важную роль играет также время, необходимое на осуществление вычислений. Поэтому в качестве алгоритма выделения новых объектов от фона целесообразно использовать первый или второй вариант.

Таблица 1

Результаты для различных алгоритмов выделения фона

В качестве признака для сравнения и отсеивания окон-гипотез используется 64-битный вектор, аналогичный бинаризованному нормализованному градиенту, описанному в [3]. Он необходим для того, чтобы убрать из изображения высокочастотную информацию, оставив только низкочастотную структуру. Алгоритм получения вектора состоит из следующих шагов:

1. Уменьшение размера до 8×8 точек независимо от первоначального размера или соотношения сторон изображения.

2. Перевод изображения в оттенки серого.

3. Вычислить среднее значение для всех 64 компонентов вектора.

4. Преобразовать все значения в биты, т.е. осуществить операцию бинаризации. Если значение компонента вектора больше среднего значения, он устанавливается в 1, в обратном случае 0.

5. Перевести отдельные биты в одно 64-битное значение.

6. Сравнить степень различия двух векторов, используя расстояние Хэмминга.

Даже после удаления части гипотез на всех предыдущих шагах остается большое количество окон-кандидатов, поэтому необходимо применить еще один этап отсеивания изображений-гипотез по цветовому профилю. В табл. 2 показана зависимость времени выполнения алгоритма и количества генерируемых гипотез от каждого из предложенных улучшений.

Следующая часть эксперимента заключалась в том, чтобы проверить, как изменится качество работы сети при использовании нейронов высоких порядков на различных ее слоях. В таких нейронах вместо обычного взвешенного суммирования используются функции высоких порядков – квадратные, кубические, тригонометрические и т.д.

Результат использования полиномиальных сумматоров может сильно отличаться в зависимости от многих условий, и зависит от конкретной задачи распознавания, конкретной архитектуры сети и того, на каком слое выбранной архитектуры эти сумматоры располагаются. Если конкретный слой со стандартными линейными сумматорами мог проводить нужные разделяющие поверхности и выделять необходимые признаки, то введение полиномиальных сумматоров не будет оказывать положительного действия на качество распознавания. Если же потенциал слоя со стандартной архитектурой был раскрыт недостаточно, и разделяющие поверхности не были построены с достаточной точностью, то нейроны высших порядков могут существенно улучшить ситуацию. На рис. 2 приведены результаты работы сети.

Таблица 2

Замер затрачиваемого времени и числа генерируемых гипотез для простого примера

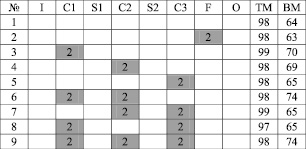
Рис. 2. Результаты экспериментов: ТМ – тестовое множество, ВМ – валидационное множество, I – входной слой, C1-C3 – сверточные слои, S1-S2 – субдискретизирующие слои, F – полносвязный слой, O – выходы сети

Добавление нейронов высоких порядков на полносвязный выходной слой не дало значительного увеличения точности распознавания, хотя для многослойного персептрона добавление полиномиальных нейронов приводит к существенному улучшению работы сети [2]. Установка нейронов высоких порядков на S-слои не имеет смысла и может привести только к излишнему усложнению вычислений. Наибольшее влияние на качество распознавания образов произвело внедрение нейронов высших порядков на первый сверточный слой, и чем дальше находится слой с нейронами второго порядка от входа сети, тем это влияние становится меньше. Использование сумматоров на первом и втором слоях дает существенно больший прирост качества обучения, чем позиционирование на втором и третьем сверточных слоях сети. Добавление третьего полиномиального слоя не приводит к каким-либо позитивным изменениям и является излишним усложнением архитектуры сети и вычислений.

Внедрение сверточных слоев высокого порядка в нейронную сеть влечет за собой увеличение алгоритмической сложности модели и времени, требуемого на распознавание. Поэтому третьим этапом эксперимента было ускорение сверточной нейронной сети второго порядка с применением процессоров векторно-матричной архитектуры.

Ускорение сверточной нейронной сети первого порядка с помощью процессоров NeuroMatrix описано в [1]. При использовании сумматоров второго порядка алгоритм вычисления карт признаков будет модифицирован с учетом выполнения следующих шагов для каждого нейрона:

1. Рабочая и Теневая матрицы разбиваются на ячейки 4×4. Возможно разбиение на большее число ячеек, но такой подход увеличивает риск переполнения единиц памяти при обработке больших массивов данных.

2. Загружаются весовые коэффициенты W и входы нейрона X, выполняется операция взвешенного суммирования, полностью аналогичная вычислениям в стандартной модели нейронов.

3. После этого вектор входных значений модифицируется с помощью операции маскирования, превращаясь в четыре новых вектора, содержащих по одному входному значению в нужных позициях.

4. Сформированный вектор квадратов входных значений загружается в рабочую матрицу, повторяется операция взвешенного суммирования с весовыми коэффициентами второго уровня.

5. Результат обрабатывается активационной функцией. На рис. 3 приведена обобщенная схема этого алгоритма.

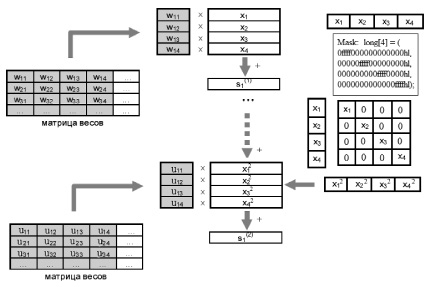
Рис. 3. Схема вычисления взвешенных сумм нейрона второго порядка

Таблица 3

Замеры скорости для разных архитектур нейронных сетей

Таблица 4

Сравнение

При использовании сравнительно небольшой выборки размером 24 000 обучающих примеров и 8-ми эпох обучения, только на прямые проходы сети потребуется

24 000∙8∙0,068 = 13056 секунд = 217,6 минут = 3,63 часов.

Если же нейронная сеть обучается на выборке NORB, содержащей 291 600 снятых с двух камер примеров, то время обработки возрастает до

291 600∙8∙2∙0,068 = 317260,8 секунд = 5287,68 минут = 88,128 часов.

Для стандартной сети ускорение прямого прохода за счет использования векторной архитектуры составляет примерно 6 %, для сверточной – 12 % [1].

В табл. 3 замеры скорости работы для полносвязных сетей с 512 и 1024 нейронами в скрытом слое, классической сверточной нейронной сети, сверточных сетей высокого порядка.

В табл. 4 приведены результаты сравнения быстродействия с процессором Intel Core i3-2130, CPU = 3,50 GHz. В зависимости от размеров выборки выигрыш в скорости может достигать 600 минут и более (для выборки NORB) и в среднем равен 11,8 %.

Выводы

1. Разработана улучшенная модель R-CNN, работающая в режиме, приближенном к реальному времени, без существенных потерь качества распознавания.

2. Разработан оптимизированный алгоритм селективного поиска объектов на изображении, работающий с ускорением до 150 % за счет уменьшения количества генерируемых гипотез.

3. Разработана и протестирована модель сверточной нейронной сети второго порядка с сумматорами высоких порядков на определенных слоях сети, улучшающая качество распознавания на 10 %.

4. Разработан способ ускорения сверточных нейронных сетей второго порядка на 11,9 % с использованием векторно-матричных процессоров.

Рецензенты:

Лубенцов В.Ф., д.т.н., профессор кафедры «Информационные системы, электропривод и автоматика», Невинномысский технологический институт, ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Невинномысск;

Тебуева Ф.Б., д.ф.-м.н., доцент, заведующая кафедрой прикладной математики и компьютерной безопасности, Институт информационных технологий и телекоммуникаций, ФГАОУ ВПО «Северо-Кавказский федеральный университет», г. Ставрополь.

Библиографическая ссылка