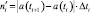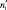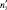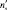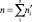Элементы электроснабжения в процессе эксплуатации оказываются под воздействием неблагоприятных факторов: повышенной влажности, агрессивных сред, пыли, переменных атмосферных явлений, а также механических и электрических нагрузок. При этом изменяются основные свойства материалов элементов, что приводит к возникновению коротких замыканий, т.е. к перерывам в подаче электрической энергии. Перерывы в электроснабжении приводят к простою производства, снижению объема выпуска продукции, увеличению затрат из-за порчи основного технологического оборудования и т.п. В литературе по надежности электроснабжения чаще всего рассматриваются вопросы исследования эксплуатационной надежности элементов электроснабжения для установившегося режима работы (период нормальной эксплуатации). Материал по исследованию надежности элементов в периоды приработки и аварийного износа встречается крайне редко, что подчеркивает необходимость рассмотрения данного вопроса.
В статье рассмотрен метод определения параметров математической модели надежности по статистическому материалу. Предлагаемый метод позволяет, используя наработки на отказ исследуемых элементов в период их приработки, рассчитать параметры модели надежности и в последующем произвести их корректировку по критериям согласия.
При исследовании надежности однотипных элементов электроснабжения получают статистический материал в виде выборок генеральной совокупности наработок на отказ по однотипным элементам. Тогда характеристикой надежности элементов является средняя наработка на отказ Тср, а математической моделью надежности является закон распределения среднего времени наработки на отказ [3]:
Q(t) = P(Тср < t). (1)
Выдвигается гипотеза о предполагаемом виде закона распределения, которая подтверждается или опровергается известными методами математической статистики с помощью критериев согласия Колмогорова, Пирсона и др.
Гипотеза о виде закона распределения выдвигается на основании каких-либо теоретических или практических предположений. В данном случае рассматривается так называемый период приработки, началом которого принято считать момент ввода новых объектов в эксплуатацию, а окончанием – начало периода нормальной эксплуатации с постоянной интенсивностью отказов.
В начале эксплуатации наблюдается повышенная интенсивность отказов, по мере приработки она снижается до некоторого уровня, после чего она остается практически постоянной длительное время (период нормальной эксплуатации) до наступления периода аварийного износа.
Известно, что такой характер интенсивности отказов элементов в период приработки объясняется тем, что в начале эксплуатации элементов быстро выявляются скрытые дефекты материалов и заводской сборки. По мере выявления и устранения вышеуказанных дефектов интенсивность отказов исследуемых элементов снижается и стабилизируется на определенном уровне, который поддерживается постоянным путем реализации плановых технических обслуживаний.
С учетом вышеуказанных рассуждений закон распределения среднего времени наработок на отказ или вероятность отказа элементов могут быть представлены в виде закона Вейбулла – Гнеденко при коэффициенте формы m < 1 или в виде суперпозиции двух экспоненциальных законов [5].
Рассмотрим в качестве модели суперпозицию двух экспоненциальных законов.
Вероятность отказа элементов имеет вид
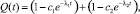 (2)
(2)
где принимаем λ1 < λ2.
Выразим принятую модель через дифференциальную функцию распределения, называемую в теории надежности частотой отказов
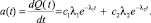 (3)
(3)
Между величинами c1 и c2 имеется связь
c1 + c2 = 1. (4)
Средняя наработка на отказ в период приработки рассчитывается как
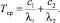 (5)
(5)
Вероятность безотказной работы
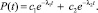 (6)
(6)
Интенсивность отказов в рассматриваемый период
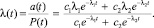 (7)
(7)
На рис. 1 представлен пример из [5] зависимости λ(t), которую можно получить, используя выражение (7).
Определим начальную интенсивность отказов.
При t = 0 имеем
λ0 = λ(0) = c1λ1 + c2λ2. (8)
Учитывая, что λ2 > λ1, можно утверждать, что к завершению периода приработки величина 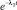 стремится к 0 быстрее, чем
стремится к 0 быстрее, чем 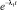 . Таким образом, при достаточно большом времени t можно пренебречь членами с λ2t, т.е. с ростом t интенсивность отказов λ(t) → λ1 = const. Это соответствует окончанию периода приработки и началу периода нормальной эксплуатации.
. Таким образом, при достаточно большом времени t можно пренебречь членами с λ2t, т.е. с ростом t интенсивность отказов λ(t) → λ1 = const. Это соответствует окончанию периода приработки и началу периода нормальной эксплуатации.
Данные рассуждения позволяют использовать в качестве математической модели надежности элементов электроснабжения в период приработки суперпозицию двух экспоненциальных законов.
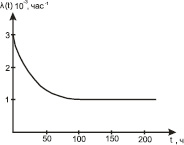
Рис. 1. Интенсивность отказов элементов в период приработки от 0 до 100 часов в случае суперпозиции двух экспоненциальных законов с параметрами: λ1 = 0,001 ч–1, λ2 = 0,040 ч–1, c1 = 0,95, и c2 = 0,05 [3]
После проверки статистических данных на однородность выборок по однотипным элементам исследования возникает вопрос в определении параметров модели, т.е. в подборе, c1, c2, λ1 и λ2 [1, 4].
Исходным статистическим материалом для подбора параметров модели является репрезентативная выборка эмпирических частот (наработок на отказ) в принятых s временных интервалах, полученная после объединения исходных выборок по всем исследуемым однотипным объектам. Представим ее в табличной форме.
Таблица 1
Репрезентативная выборка эмпирических частот
|
∆ti |
∆t1 |
∆t2 |
... |
… |
∆ts |
|
ni |
n1 |
n2 |
… |
… |
ni |
где ∆ti – варианты принятых s временных интервалов наработок на отказ; ni – эмпирические частоты (наработки на отказ) в принятых s интервалах времени.
Используя статистический материал, определим предварительные значения параметров модели: c1, c2, λ1 и λ2.
В качестве предварительного значения параметров λ1 и λ2 принимаем соответственно: 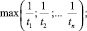 и
и 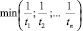 .
.
Из формулы (8) находим c1 и c2:
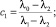
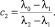 (9)
(9)
Используя формулу (3), изображаем предварительную математическую модель в виде теоретической зависимости a(t) (рис. 2).
Известно, что элементы электроснабжения обладают достаточно высокой надежностью. Так, например, по справочным данным интенсивности отказов основных элементов электроснабжения (воздушные и кабельные линии на 1 км длины, силовые трансформаторы, ячейки выключателя, разъединителя и короткозамыкателя, а также шины РУ на одно присоединение) находятся в интервале от 0,001 до 0,03 отказа в год. Учитывая эту особенность и зависимость λ(t) = a(t)/P(t), при P(t) ≈ 1, можно утверждать, что λ(t) ≈ a(t).
Таким образом, частота отказов элементов электроснабжения в функции времени будет соответствовать интенсивности отказов, которая чаще используется на практике для характеристики надежности объектов.
Для количественной оценки гипотезы о соответствии принятой модели опытным данным необходимо выполнить расчеты теоретических и эмпирических частот. Расчеты выполним в табличной форме (табл. 2, 3).
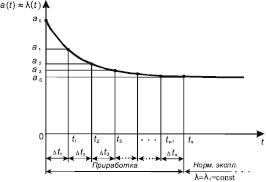
Рис. 2. Теоретическая зависимость частоты (а) или интенсивности (λ) отказов объектов от времени в период приработки
Таблица 2
Эмпирические частоты
|
Номер интервала |
Границы интервала |
Частота эмпирическая (число отказов в i-м интервале) |
|
|
i |
ti |
ti + 1 |
ni |
|
1 |
x0 |
x1 |
n1 |
|
2 |
x1 |
x2 |
n2 |
|
... |
... |
... |
... |
|
s |
xs-1 |
xs |
ns |
|
(общее число отказов за период приработки) |
|||
Таблица 3
Расчет теоретических частот суперпозиции двух экспоненциальных законов
|
Номер интервала |
Границы интервала |
a(t) |
Теоретическая частота |
||
|
i |
ti |
ti + 1 |
a(ti) |
a(ti + 1) |
|
|
1 |
x0 |
x1 |
a(t0) |
a(t1) |
|
|
2 |
x1 |
x2 |
a(t1) |
a(t2) |
|
|
… |
… |
… |
… |
… |
… |
|
s |
xs-1 |
xs |
a(ts–1) |
a(ts) |
|
|
|
|||||
Для вычисления теоретических частот 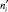 , ось времени зависимости a(t) (рис. 2) разбиваем на s интервалов в соответствии с табл. 1. Суммарная продолжительность интервалов должна соответствовать времени приработки объектов от t = 0 до момента наступления постоянной интенсивности отказов λ1 (начало периода нормальной эксплуатации).
, ось времени зависимости a(t) (рис. 2) разбиваем на s интервалов в соответствии с табл. 1. Суммарная продолжительность интервалов должна соответствовать времени приработки объектов от t = 0 до момента наступления постоянной интенсивности отказов λ1 (начало периода нормальной эксплуатации).
Тогда теоретические частоты в заданных интервалах времени определятся по формуле
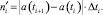 (10)
(10)
Простейшим способом проверки гипотезы о виде закона распределения является графический способ.
На рис. 3 приведено графическое сравнение теоретических частот с эмпирическими частотами по данным табл. 2 и 3.
Графический метод нагляден, но не позволяет измерить степень соответствия или согласия.
Выполним количественную оценку согласия, используя критерий Пирсона.
Методика проверки гипотезы по этому критерию согласия приведена в [2].
Если в результате вычислений наблюдаемого значения критерия хи квадрат 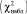 и критического значения
и критического значения 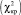 на принятом уровне значимости α было получено неравенство
на принятом уровне значимости α было получено неравенство 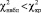 , то делается вывод о том, что данные наблюдений хорошо согласуются с гипотезой о справедливости принятой математической модели надежности – суперпозиции двух экспоненциальных законов в период приработки.
, то делается вывод о том, что данные наблюдений хорошо согласуются с гипотезой о справедливости принятой математической модели надежности – суперпозиции двух экспоненциальных законов в период приработки.
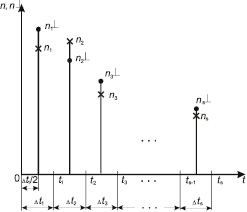
Рис. 3. Графическое сравнение эмпирических (ni) и теоретических частот 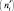
В случае получения результата 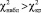 необходимо скорректировать параметры принятой математической модели – изменить значения c1, c2, λ1 и λ2 и повторять все расчеты для получения неравенства
необходимо скорректировать параметры принятой математической модели – изменить значения c1, c2, λ1 и λ2 и повторять все расчеты для получения неравенства 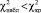 .
.
Расчеты целесообразно выполнять на ЭВМ, для этой цели разработана программа вычислений.
Выводы
1. Предложена методика для определения параметров математической модели надежности объектов в период приработки.
2. Данная методика позволяет с высокой точностью подобрать параметры модели путем их вариации с последующей проверкой соответствия модели опытным данным, применяя критерий согласия Пирсона.
3. Модель может быть окончательно уточнена после входа объекта в период нормальной эксплуатации. Тогда в качестве λ1 можно принять интенсивность отказов экспоненциального закона λ или величину
Тср = 1/λ,
где Тср – средняя наработка на отказ объекта в период нормальной эксплуатации.
4. Разработанная математическая модель надежности объектов позволит нормировать показатели надежности элементов электроснабжения в период приработки, выбирать способы повышения надежности электроснабжения за счет резервирования ответственных элементов и оптимизировать техническое обслуживание.
Рецензенты:
Черепанов В.В., д.т.н., профессор кафедры электроснабжения, ФГБОУ ВПО «Вятский государственный университет», г. Киров;
Красных А.А., д.т.н., профессор, заведующий кафедрой электротехники и электроники, ФГБОУ ВПО «Вятский государственный университет», г. Киров.
Библиографическая ссылка
Басманов В.Г., Закалата А.А., Холманских В.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НАДЕЖНОСТИ ЭЛЕМЕНТОВ ЭЛЕКТРОСНАБЖЕНИЯ В ПЕРИОД ПРИРАБОТКИ // Фундаментальные исследования. 2015. № 5-2. С. 247-251;URL: https://fundamental-research.ru/ru/article/view?id=38201 (дата обращения: 28.02.2026).




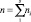
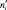 в i-м интервале
в i-м интервале