Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Хассанин Хатем Мохамед Абдель Максуд 1

---

1 Национальный исследовательский Томский политехнический университет

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. Большее количество задач сводятся к задачам оптимизации: безусловная оптимизация нелинейных функций; метод наименьших квадратов; решение нелинейных уравнений; линейное программирование; квадратичное программирование; условная минимизация нелинейных функций; минимакский метод; многокритериальная оптимизация. В свете этих положений актуальность данной работы очевидна и заключается в необходимости рассмотрения решения задач оптимизации с помощью нейронной сети. Реализация численных алгоритмов осуществлялась посредством программ Matlab. Нейронная сеть представляет собой систему «нейронов», взаимодействующих между собой наподобие настоящей нейронной сети мозга. «Нейрон» в данном случае представляется неким обладающим состоянием вычислительным процессом, так что сеть может работать параллельно. Искусственная сеть «обучается» решению некоторой задачи, что, по сути, сводится к вычислениям весовых коэффициентов матрицы, без всякой «магии». С помощью нейронных сетей пытаются решать различные задачи. Целью написания данной работы явилось изучение решения задач оптимизации с помощью нейронной сети Хопфилда.

Статья в формате PDF

742 KB

оптимизация

полусфера

устойчивая точка

бассейн аттрактора

нейронная сеть Хопфилда

1. Галушкин А.И. Нейронные сети: основы теории. – М.: Горячяя линия Телеком, 2010. С. 57.

2. Исакова О.П., Тарасевич Ю.Ю., Юзюк Ю.И. Обработка и визуализация данных физических экспериментов с помощью пакета «Origin» – М.: Книжный дом «ЛИБРОКОМ», 2009. – С. 33.

3. Мкртчян С.О. Нейроны и нейронные сети (Введение в теорию формальных нейронов. – М.: Энергия, 2010. – С. 114.

4. Мищенко В.А. Обучение искусственных нейронных сетей // Современные проблемы науки и образования. – Воронеж: ВГПУ, 2009. –№ 6. – С. 9.

5. Протасов С.И. Методы и алгоритмы анализа, передачи и визуализации данных в системах компьютерного стереозрения: автореф. дис. ... канд. техн. наук. – Воронеж, 2013. – С. 9.

6. Хохлова Т.Н. Устойчивость нейронных сетей Хопфилда с запаздыванием // Математическое моделирование и краевые задачи: труды седьмой Всероссийской научной конференции с междуна родным участием. – Самара: 2010. – С. 277.

7. Хохлова Т.Н. Устойчивость полносвязной и звездной структур нейронных сетей // Вестник ЮУрГУ, серия «Математика Механика Физика». – 2012. – Т. 34. – С. 195.

8. Хохлова Т.Н. Устойчивость нейронных сетей стандартных конфигураций // Статистика Моделирование Оптимизация. Сборник трудов Всероссийской конференции. – Челябинск, 2011. – С. 331.

9. Kaslik E. Complex and chaotic dynamics in a discrete-time-delayed Hopfield neural Network with ring architecture / E. Kaslik, S. Balint // Neural Networks. – 2009. – Vol. 22 (10). – P. 1411.

Нейронная сеть представляет собой систему «нейронов», взаимодействующих между собой наподобие настоящей нейронной сети мозга. «Нейрон» в данном случае представляется неким обладающим состоянием вычислительным процессом, так что сеть может работать параллельно. Искусственная сеть «обучается» решению некоторой задачи, что, по сути, сводится к вычислениям весовых коэффициентов матрицы. С помощью нейронных сетей искусственная сеть пытается решать различные задачи.

Целью данной работы явилось решение задачи оптимизации с помощью нейронной сети программы Matlab [2]. Достижение поставленной цели может быть реализовано посредством решения следующих задач:

1. Формирование основ работы нейронных сетей.

2. Выделение проблем, возникающих при решении задач оптимизации с помощью нейронной сети Хопфилда.

Выбор оптимального решения проводится, как правило, с помощью некоторой функции, называемой целевой функцией. Целевую функцию можно записать в виде

u = f(x), x ∈ G,

где G – некоторая область ограничений.

Джон Хопфилд в 1982 году привлек к анализу нейронных сетей мощный аппарат статистической физики (на основе аналогий между нейронными сетями и особыми физическими системами – спиновыми стеклами). Спиновые стекла – это ансамбли электромагнитных частиц, находящихся на переходе фаз, например на нижней точке плавления стекла. Каждая частица обладает собственным моментом количества движения, называемым спином. Спин может иметь только две ориентации S1, S2 относительно внешнего магнитного поля, направленного по некоторой оси x. Одна из них совпадает с направлением поля (S1 = 1), а другая – ему противоположна (S2 = –1). Рассмотрим теперь пример из области нейронных сетей, в частности обучение элементарного перцептрона распознаванию двух изображений, например, букв П и Г (рис. 1) [6].

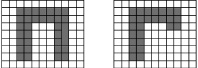
Рис. 1. Эталонные обучающие изображения букв

В процессе обучения сети возникают две стационарные точки или два аттрактора. Бассейны аттракторов создаются всеми изображениями букв П и Г с различными дефектами. Эти изображения совместно с эталонными многократно предъявляются перцептрону в процессе обучения сети, когда фактически по двум заданным стационарным точкам, используя итерационную процедуру, пытаются найти подходящую матрицу весов связей нейросети.

Определение 1. Состояние

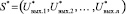(1)

нейросети называется устойчивым по отношению к произвольному подмножеству M1 элементов сети, если оно не изменяется при одновременном срабатывании любых его отдельных нейронов.

Определение 2. Состояние S* нейросети называется устойчивым или стационарным, если оно устойчиво по отношению к асинхронному срабатыванию любых отдельных нейронов и одновременному срабатыванию всех элементов сети.

Определение 3. Прямая задача стационарности для нейронных сетей состоит в определении всех стационарных состояний нейросети по заданной матрице весов связей W и вектору порогов θ (или вектору смещений W0) нейронов.

Определение 4. Обратная задача стационарности для нейронных сетей состоит в том, чтобы по заданному множеству

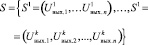(2)

стационарных состояний сети определить матрицу весов связей W и вектор порогов θ (или вектор смещений W0), обеспечивающих эти стационарные состояния [4].

Все стационарные состояния нейросети теоретически можно определить из системы уравнений, описывающей все компоненты сети. Для этого достаточно выбрать начальное состояние S0 всех нейронов сети и, используя заданный режим их срабатывания, определить новое состояние S1 сети, затем, воспользовавшись S1 в качестве следующего начального состояния, определить состояние S2 и т.д. В результате этого процесса возникает последовательность состояний сети:

S0, S1, S2, …, Sk, … (3)

Определение 5. Цикл состояний нейросети, не имеющий внутри себя других циклов, называется минимальным. Очевидно, что любые два минимальных цикла либо совпадают, либо не имеют общих состояний.

Определение 6. Бассейном BS притяжения цикла Cr (или бассейном аттрактора) называется совокупность всех состояний нейронной сети, которые притягиваются к данному циклу: 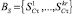. Бассейны притяжения любых двух циклов Ck, Cm . C не пересекаются, то есть 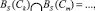если k ≠ m, а объединение бассейнов всех циклов равно множеству всех состояний S нейронной сети [9]:

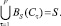
В графической интерпретации бассейны аттракторов включают в себя состояния (или точки), соответствующие минимальному циклу, и деревья, стягивающиеся к состояниям или точкам цикла (рис. 2) [3].

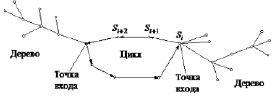
Рис. 2. Бассейн аттрактора

Точки цикла, имеющие непустые деревья, называются точками входа в цикл. Деревья разных точек входа не пересекаются, а их совокупность покрывает весь бассейн аттрактора.

Хопфилд впервые рассмотрел полно связную нейронную сеть, состоящую из бинарных элементов с симметричными связями. Структура этой сети приведена на рис. 3 [7].

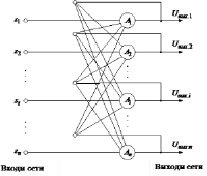
Рис. 3. Нейронная сеть Хопфилда

Дискретная сеть Хопфилда состоит из единственного слоя нейронов, каждый из которых связан со всеми остальными и имеет сетевые вход и выход. Сигналы на сетевых входах нейронов определяют их выходные сигналы [1]:

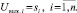
При отсутствии сигналов на сетевых входах элементы сети функционируют в асинхронном режиме, при котором каждый из них определяет свой выходной сигнал в случайные моменты времени с заданной средней частотой в соответствии с выражением

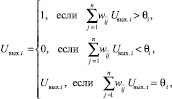(5)

где Uвых.i > θi – соответственно выходной сигнал и порог i-го нерона; wji – вес связи между j-м и i-м нейронами.

Матрица 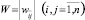весов связей нейросети симметрична и имеет нулевые компоненты на главной диагонали, то есть

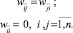(6)

Такой вид матрицы весов обеспечивает устойчивость сети: при подаче на ее входы внешних сигналов возникает последовательность состояний сети вида (3), которая оканчивается стационарным состоянием. Процесс достижения стационарного состояния можно описать с помощью минимизации специальной энергетической функции:

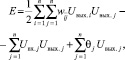(7)

где E – искусственная энергия сети, заданная в виде функции Ляпунова; Uвх.j – внешний входной сигнал j-го нейрона.

Энергию всей сети можно представить как сумму энергий ее отдельных нейронов:

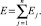(8)

Из выражений (8) и (7) имеем [8]

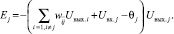
Рассмотрим изменение энергии ΔEj произвольного j-го элемента при его срабатывании:

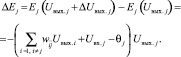(9)

Для бинарных нейронов приращения их выходных сигналов может принимать только три значения: +1, 0, –1. При этом знак приращения ΔUвых.j для j-го элемента совпадает со знаком выражения в круглых скобках. Действительно, если ΔUвых.j = –1, то есть нейрон переходит из единичного состояния в нулевое, то это означает, что в соответствии с выражением (5) выполняется неравенство

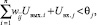
то есть выражение в круглых скобках соотношения (9) отрицательно. Если ΔUвых.j = 1, то рассматриваемый j-й нейрон переходит из нулевого состояния в единичное и, следовательно,

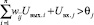
или

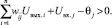
Из совпадения знаков сомножителей в выражении (9) следует, что при срабатывании любого j-го нейрона ни его энергия, ни энергия всей сети увеличиться не может. Она либо остается прежней, если ΔUвых.j = 0, либо уменьшается, если ΔUвых.j = 0. Следовательно, по мере срабатывания нейронов энергия будет монотонно убывать, пока не достигнет одного из своих локальных минимумов, которому соответствует одна из стационарных точек нейросети. Эволюция сети из любого начального состояния в силу существования функции Ляпунова (7) всегда кончается в одной из ее стационарных точек, то есть аттракторами в дискретной бинарной сети Хопфилда являются только стационарные точки. Это же утверждение справедливо и для дискретной сети Хопфилда с биполярными нейронами.

Для хранения некоторого множества изображений 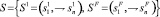в биполярной сети Хопфилда используется матрица W весов связей с элементами

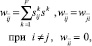(10)

где индекс k указывает на принадлежность входных сигналов k-му изображению. При переходе к бинарным нейронам элементы wij матрицы W определяются соотношением

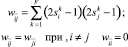. (11)

Пороги qi всех бинарных элементов обычно принимаются равными нулю, а пороги биполярных нейронов часто определяются через сумму элементов матрицы весов:

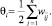(12)

Для сети Хопфилда число p запоминаемых изображений не должно превышать величины, примерно равной 0,15n, где n – число нейронов сети.

Кроме того, если есть пары очень похожих изображений, например Sk, Sθ, то они могут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети изображения Sk может приводить к появлению на ее выходе изображения Sθ и наоборот.

Задачи, решаемые дискретной сетью Хопфилда с бинарными или биполярными нейронами в качестве ассоциативной памяти, формулируются следующим образом: известен набор эталонных двоичных изображений или сигналов. Сеть должна уметь по частичной информации неидеальных изображений, подаваемых на ее вход, выделять эталонные изображения или давать информацию о том, что входной вектор не соответствует ни одному из хранимых в ее памяти. Когда сеть распознает какое-либо изображение, то на ее выходах появляется именно это изображение. В противном случае вектор выходных сигналов не совпадает ни с одним из эталонных [5].

Пример. Рассмотрим возможности дискретной сети Хопфилда с девятью биполярными нейронами по распознаванию неидеальных изображений букв Н и Т. Эталонные изображения S1и S2 этих букв приведены на рис. 4, там же дана нумерация элементов изображений, соответствующая нейронам сети Хопфилда и их векторному представлению.

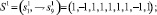
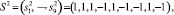
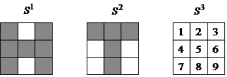
Рис. 4. Изображения S1, S2, S3

В соответствии с исходными данными выражение (11) для рассматриваемого примера принимает вид

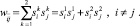
Рассчитаем вес связи w12: w12 = 1 (–1) + 1,1 = 0.

В силу общего равенства также получим, что w21 = w12 = 0. Аналогично рассчитываются и остальные элементы матрицы W весов связей. Элементы главной диагонали матрицы W определяются выражением (10) при i = j: w11 = w22 = … = w99 = 0. Результаты расчетов матрицы W приведены в табл. 1.

Пороги биполярных нейронов сети Хопфилда рассчитываются с помощью соотношения (12) и данных табл. 1:

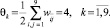
Предъявим сети Хопфилда изображение S1 буквы Н и рассчитаем выходные сигналы сети после его снятия при двух значениях порогов: θk = 4 и θk = –4. Результаты расчетов приведены в табл. 2.

Из анализа данных табл. 2 следует, что вектор выходного изображения сети повторяет изображение S1 в широком диапазоне значений порогов. Аналогичная ситуация получается и при предъявлении изображения S2 буквы Т (табл. 3), то есть рассчитанная дискретная сеть Хопфилда, как ей и положено, повторяет на своем выходе идеальные входные изображения.

Предъявим теперь сети изображение S3И, инверсное изображению S3 (рис. 5). Изображение S3 И можно рассматривать как искаженное представление буквы Н, у которого утеряны две отрицательные компоненты. Результаты расчетов для этого случая при θk = –4 приведены в табл. 4 (при θk > 2 изображение не восстанавливается). Сопоставление пятых столбцов табл. 4 и 2 показывает, что сеть восстановила эталонное изображение буквы Н.

Таблица 1

Матрица весов связей

Таблица 2

Результаты расчетов выходных сигналов сети Хопфилда после предъявления изображения S1 буквы Н

Таблица 3

Результаты расчетов выходных сигналов сети Хопфилда после предъявления изображения S2 буквы Т

Таблица 4

Результаты расчетов выходных сигналов сети Хопфилда после предъявления изображения S3

Таким образом, мы можем прийти к выводу, что при предъявлении в пакете Matlab изображений S1, S2, S3 и сеть попадала в стационарную точку за один такт времени при синхронном срабатывании всех ее элементов.

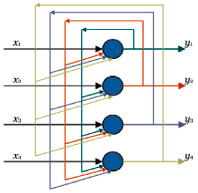
Рис. 5. Четырёхнейронные сети Хопфилда

Нейронная сеть функционирует циклически. Каждый из четырёх нейронов сети Хопфилда имеет выходы сигнала, который подается на входы всех остальных нейронов, кроме себя самого.

Однако эту сеть нельзя научить практически ничему. Сеть, содержащая N нейронов, может запомнить не более ~0,15∙N образов. Таким образом, реальная сеть должна содержать достаточно внушительное количество нейронов. Одним из существенных недостатков сети Хопфилда является небольшая ёмкость. Плюс ко всему образы не должны быть очень похожи друг на друга, иначе в некоторых случаях возможно зацикливание при распознавании.

Заключение

Подводя итог проведенного исследования, можно сформулировать следующие выводы и предложения по данной теме.

1. Каждый нейрон сети в нейронной сети Хопфилда получает и передаёт сигналы другим. Связь нейронов зависит от типа сети. Сеть Хопфилда является однослойной сетью, потому что в ней используется лишь один слой нейронов. Она также является рекурсивной сетью, потому что обладает обратными связями.

2. Решение задач оптимизации с помощью нейронной сети посредством программы Matlab реализуется через образ, который сеть запоминает или распознаёт (любой входной образ), образ может быть представлен в виде вектора X размерностью n, где n – число нейронов в сети. Выходной образ представляется вектором Y с такой же размерностью. Каждый элемент вектора может принимать значения: +1 либо –1 (можно свести к 0 и 1, однако + 1 и –1 удобнее для расчётов).

Рецензенты:

Фокин В.А., д.т.н., доцент, профессор кафедры биологической и медицинской кибернетики, ГБОУ ВПО «Сибирский государственный медицинский университет» Министерства здравоохранения и социального развития Российской Федерации, г. Томск;

Берестнева О.Г., д.т.н., профессор кафедры прикладной математики, Институт кибернетики ТПУ, г. Томск.

Библиографическая ссылка