Дальнейшее совершенствование лазерных интерферометрических систем, используемых на объектах специальной техники, требует от проектировщиков создания средств измерений с использованием новых материалов и методов измерений, физических эффектов и явлений, а также совершенствования приемов конструирования и технологических процессов. Одним из таких направлений следует считать внедрение волоконно-оптических технологий [1].
В России ведутся работы по совершенствованию и созданию различных волоконно-оптических устройств, систем, их компонентов и технологии изготовления самих оптических волокон. Достаточно отработаны и уже широко используются волоконно-оптические телекоммуникационные системы. Ведутся интенсивные разработки в области создания волоконно-оптических лазерных интерферометрических систем, обеспечивающих более эффективную передачу информации о состоянии объекта в сравнении с традиционными системами сбора и преобразования информации в условиях воздействия сильных электромагнитных помех и повышенной взрывоопасности [2, 6].
Существенным достоинством таких систем является то, что в силу высокой частоты электромагнитных волн оптического диапазона пропускная информативная способность одного канала связи по оптическому волокну может быть существенно больше, чем при использовании канала в радиодиапазоне. Поэтому разработке и созданию этих систем в настоящее время уделяется большое внимание [2, 3, 5]. Поскольку в этих системах имеются источник излучения, среда распространения, фотоприемник и электронный тракт усиления и обработки сигнала, они могут и должны быть отнесены к оптоэлектронным системам [4, 7].
Как по сечению, так и вдоль волокна коэффициент преломления может изменяться, и поэтому средняя скорость прохождения луча по разным трассам будет различна. Это обстоятельство приводит к еще большему расширению импульса на выходе волокна.
Если диаметр сердцевины волокна равен или меньше длины волны распространяющегося излучения dc ≤ λ, то характер распространения излучения меняется. В таких волокнах возможен одномодовый режим, когда по сердцевине распространяется одна мода излучения.
При этом даже при полном внутреннем отражении на границе сердцевины и оболочки интенсивность электромагнитного поля в оболочке и за ее пределами не равна нулю и часть потока излучения распространяется по оболочке.
Диаметр оптического волокна, в пределах которого переносится 99 % потока излучения в одномодовом режиме, называется оптическим диаметром волокна. Этот диаметр может быть больше внешнего диаметра волокна. Следовательно, в жгутах, собранных из тонких волокон, принципиально будет наблюдаться просачивание электромагнитного поля в соседние волокна. Если жгут является когерентным и имеет гексагональную упаковку (т.е. каждое волокно соприкасается с шестью окружающими волокнами), то доля мощности, проникающей в соседние волокна, приблизительно может быть оценена по формуле [6, 8]
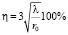 , (1)
, (1)
где 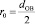 – радиус волокна.
– радиус волокна.
Степень когерентности и поляризация излучения при передаче по волокнам ухудшаются вследствие рассеяния излучения внутри волокон, проникновения излучения из соседних волокон, наличия рассеянного излучения при падении излучения на торец волокна, из-за искажения фронта волны. Разрушение поляризации особенно велико, если изучение внутри волокна распространяется по спирали.
Для улучшения когерентности оптического излучения на выходе оптического волокна в пространстве лазерного интерферометрического преобразователя необходимо определить условия когерентности в разрабатываемой оптической системе.
Используя подход декомпозиции, луч лазера рассматривают как множество элементарно малых лучей, толщиной которых можно пренебречь.
Задача определения условий когерентности всего светового потока сводится к определению числа отражений каждого элементарного малого луча от стенок оптического волокна.
Отражение луча показано на рис. 1.
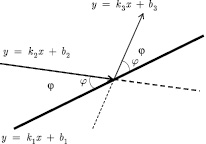
Рис. 1. Геометрические построения к расчету хода лучей
Касательная к отражающей поверхности, проведенной в точке падения луча, описывается уравнением
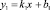 . (2)
. (2)
Тогда падающий и отраженный лучи соответственно определяются следующими уравнениями:
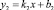 ;
;
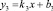 . (3)
. (3)
Соотношение косинусов падающего и отраженного лучей определяется выражением
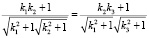 . (4)
. (4)
Выполняя преобразования, получаем
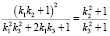 ,
,
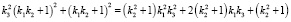 . (5)
. (5)
Уравнение относительно неизвестного k3 имеет вид
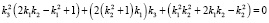 . (6)
. (6)
Решениями данного уравнения будут два угловых коэффициента прямых, образующих с касательной одинаковые углы:
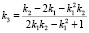 . (7)
. (7)
Данный подход обладает недостаточной вычислительной точностью в случае прямых, близких к вертикальной (угловой коэффициент начинает стремиться к бесконечности на углах, близких к 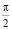 ).
).
Уравнения прямых (касательной к отражающей поверхности, падающего луча, отраженного луча) в общем виде имеют следующий вид:
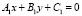 ;
;
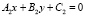 ;
;
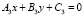 . (8)
. (8)
Нормальные векторы к соответствующим прямым описываются уравнениями (рис. 2)
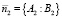 ;
; 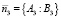 .
.
Уравнение касательной преобразуем к виду ax + by + c = 0,
где 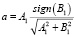 ;
; 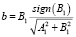 ;
;
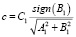 .
.
При этом a = – sin α, b = cos α, угол α – острый угол между прямой и положительным направлением оси Ox. Оператор поворота на угол α по часовой стрелке запишется в следующем виде:
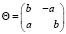 . (9)
. (9)
Данный оператор, исходя из основного тригонометрического тождества, является невырожденным с единичной нормой. Обратный оператор (поворота на угол α против часовой стрелки) имеет вид
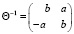 . (10)
. (10)
Рассматривая процесс отражения луча от горизонтальной поверхности, можно заметить, что горизонтальная составляющая нормального вектора луча меняется на противоположную, а вертикальная остается прежней. Оператор преобразования вектора при отражении от горизонтальной поверхности запишется
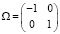 . (11)
. (11)
Поворачивая систему на угол α по часовой стрелке, нормальный вектор уравнения прямой, описывающей падающий луч, преобразуется к виду:
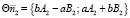 . (12)
. (12)
В новой системе координат отражающая поверхность уже горизонтальна, и нормальный вектор прямой отраженного луча имеет вид
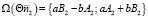 . (13)
. (13)
Возвращаясь в исходную систему координат (поворачивая на угол α против часовой стрелки), получают искомые координаты нормального вектора:
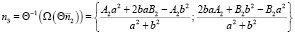 . (14)
. (14)
В силу основного тригонометрического тождества
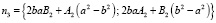 . (15)
. (15)
уравнение прямой, описывающей ход отраженного луча, имеет вид:
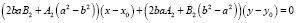 . (16)
. (16)
где (x0, y0) – координаты точки отражения.
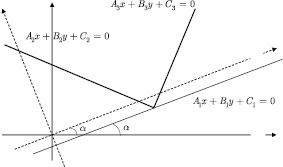
Рис. 2. Геометрические построения к выводу касательных в общем виде
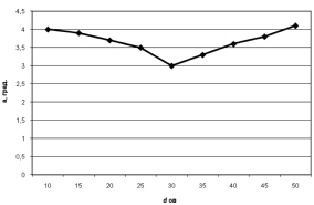
Рис. 3. График зависимости α = f(dOB)
Предположим, что угол расхождения луча не превышает α = 4 °. Необходимо определить граничные условия таким образом, чтобы на выходе из оптического волокна поток оставался когерентным.
Для выполнения условия когерентности процесс отражения элементов луча от стенок оптического волокна должен происходить одновременно для всех его элементов. Диаметр луча не должен превышать диаметра сердцевины оптического волокна, так как нарушится когерентность потока за счет отражения краевых элементов луча от стенок сердцевины оптического волокна (происходит смещение фазы колебания отраженных элементов светового потока), в то время, когда фаза остального потока остается неизменной. Наиболее эффективным способом решения данной проблемы является изгиб оптического волокна. В этом случае толщина потока перестает расти, и все элементарно малые потоки колеблются синфазно.
Соотношение для параметров проводящей оптической системы следующее:
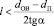 . (17)
. (17)
Исходя из существующей номенклатуры промышленно производимых оптических волокон и возможностей фокусировки пучка лазерного излучения, предположим, что диаметр пучка на порядок отличается от диаметра оптического волокна:
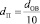 .
.
С учетом того, что tgα ≈ α, получаем
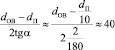 . (18)
. (18)
Результаты численного моделирования процесса прохождения луча в оптическом волокне сведены в таблице, по ним построен график зависимости α = f(dOB) (рис. 3).
Значение угла расхождения лазерного луча на выходе оптического волокна от диаметра пройденного изгиба
|
a, ° |
4 |
3,9 |
3,7 |
3,5 |
3 |
3,3 |
3,6 |
3,8 |
4,1 |
|
dизгиба |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
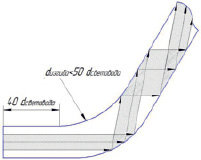
Рис. 4. Схема изгиба световода
Из анализа результатов моделирования видно, что для сохранения когерентности оптического пучка при выходе из световода необходимым является наличие изгиба радиусом не более 50 диаметров оптического волокна, с началом на расстоянии, не превышающем 40 диаметров оптического волокна от точки вхождения луча (рис. 4).
Выполненное математическое моделирование позволило выявить наличие эффекта фокусировки луча при прохождении изгиба с сохранением когерентности на достаточно больших расстояниях от входа в оптическое волокно. Это явление позволило сделать вывод о возможности создания лазерных интерференционных информационно-измерительных с оптическими волокнами, заменяющими в системах крупногабаритные элементы оптической системы.
Рецензенты:
Таранцева К.Р., д.т.н., профессор, проректор по научной работе Пензенского государственного технологического университета, г. Пенза;
Ломтев Е.А., д.т.н., профессор кафедры «Информационно-измерительная техника и метрология» Пензенского государственного университета, г. Пенза.
Библиографическая ссылка
Базыкин С.Н., Базыкина Н.А., Васильев В.А., Мурашкина Т.И., Шошкина М.Н. УСЛОВИЯ СОХРАНЕНИЯ КОГЕРЕНТНОСТИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ В ИЗОГНУТОМ ОПТИЧЕСКОМ ВОЛОКНЕ // Фундаментальные исследования. 2015. № 2-20. С. 4393-4397;URL: https://fundamental-research.ru/ru/article/view?id=38080 (дата обращения: 29.01.2026).



