Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Жук А.Ю. 1

---

1 ФГБОУ ВПО «Братский государственный университет»

В статье представлены результаты экспериментальных исследований работы устройства для сбора и транспортировки древесины в береговых зонах водохранилищ, что является необходимым элементом проектирования технологических процессов освоения древесины в береговых зонах и прибрежных акваториях водохранилищ, в частности при выборе состава оборудования для их осуществления. Для этого следует определить характеристики предложенных устройств исходя из требований обеспечения безопасности, в частности приведены регрессионные модели динамического воздействия на опоры канатной системы, закреплённые на берегу и плавучем основании, дан их анализ. После проведения теоретических исследований были получены зависимости, удовлетворяющие заданным условиям. Проведя их анализ, установили, что связи основных параметров канатной транспортирующей системы, входящей в рабочее оборудование рассматриваемых устройств, могут быть описаны степенными зависимостями, либо, учитывая диапазоны изменения исследуемых величин, полиномами второго порядка. В этой связи был реализован эксперимент с использованием метода планирования эксперимента второго порядка. Выходными параметрами являлись усилие в несущем канате и провес несущего каната. Основные влияющие факторы: диаметр несущего каната; угол наклона несущего каната; длина пролета; вес пачки лесоматериалов; скорость перемещения. Полученные уравнения для определения динамических нагрузок в зависимости от различных параметров, таких как диаметр несущего каната, угол его наклона, скорость перемещения пачки лесоматериалов, масса груза, длина пролёта, позволят задавать необходимые технологические режимы для обеспечения безопасной работы разработанных механизмов с максимальной производительностью.

Статья в формате PDF

621 KB

канатная трелёвка

динамическое воздействие

плавучее основание

«бесхозная» древесина

аварийная древесина

прибрежные акватории водохранилищ

береговая зона водохранилищ

планирование эксперимента

1. Андреев В.Н. Математическое планирование эксперимента. – Л.: ЛТА, 1982. – 39 с.

2. Горяев А.С., Жук А.Ю., Федяев А.А. Разработка новых способов очистки береговой зоны водохранилищ // Системы. Методы. Технологии. – 2011. – № 10. – С. 130–134.

3. Жук А.Ю. Технология комплексного освоения древесины в акватории и береговой зоне озер и водохранилищ // Труды Братского государственного университета. Серия: Естественные и инженерные науки. – 2014. – Т. 1. – С. 323–326.

4. Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по теории вероятностей и математической статистике. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 640 с.

5. Нгуен Ван Би. Исследование подвесных канатных установок с поворотами трасс в плане для установления рациональных параметров и технологии с целью повышения их производительности и надежности в работе. – дис. ... канд. техн. наук. – Л.: ЛТА, 1982. – 209 с.

При проектировании технологических процессов освоения древесины в береговой зоне и прибрежных акваториях водохранилищ необходимо выбрать состав оборудования для их осуществления [2, 3]. Для этого следует определить характеристики предложенных устройств исходя из требований обеспечения безопасности. После проведения теоретических исследований были получены зависимости, удовлетворяющие заданным условиям. Математические модели требуют их экспериментального подтверждения.

Цель исследований – определение усилий, возникающих в несущем канате установки для сбора и транспортировки бесхозной древесины в береговой зоне водохранилищ в зависимости от длины пролета, угла наклона несущего каната, его диаметра, веса пучка и скорости транспортировки пучка.

При обработке экспериментальных данных использовалось лицензионное программное обеспечение: Microsoft Excel 2013 и Statgraphics Centurion XVII.I. Проведя анализ теоретических зависимостей, установили, что связи основных параметров канатной транспортирующей системы, входящей в рабочее оборудование рассматриваемых устройств, могут быть описаны степенными зависимостями, либо, учитывая диапазоны изменения исследуемых величин, полиномов второго порядка. Поэтому связи был реализован эксперимент с использованием метода планирования эксперимента второго порядка. Выходными параметрами являлись усилие в несущем канате и провес несущего каната.

Основные влияющие факторы: диаметр несущего каната; угол наклона несущего каната; длина пролета; вес пачки лесоматериалов; скорость перемещения. Уровни варьирования влияющих факторов представлены в табл. 1.

Для получения необходимых зависимостей использовали ортогональный композиционный план второго порядка, матрица планирования эксперимента представлена в табл. 2.

Таблица 1

Основные факторы при проведении экспериментов по определению усилия в несущем канате и провеса несущего каната при перемещении пучка древесины

Таблица 2

Основные факторы при проведении экспериментов по определению усилия в несущем канате и провеса несущего каната при перемещении пачки лесоматериалов на лабораторной модели

Величина плеча α* определяется в зависимости от числа факторов, в нашем случае число основных факторов K = 5, таким образом, α* = 1,60717 [1].

Общее число опытов при проведении эксперимента рассчитывается по формуле

N = N_Я + N_α + N₀, (1)

где N_Я – число опытов в ядре плана (при K ≥ 5 N_Я = 2K–1, N_Я = 16), N_α – число опытов в звездных точках (N_α = 2K, N_α = 10), N₀ – число опытов в центре плана (для ортогонального композиционного плана принимается N₀ = 1), итого 27 опытов.

Для проведения опытов была адаптирована методика, описанная в работе [5]. Монтажное натяжение несущего каната в опытах составляло 1,5 кН. Динамическое усилие фиксировали при помощи динамометра при нахождении груза в середине пролета. Во всех опытах число наблюдений n = 5 было достаточным для получения оценки с доверительной вероятностью p = 95 %. Расчетное значение критерия Кохрена составляет Gр = 0,1490, что меньше табличного значения GT = 0,1500 [5] (при f = 5 – 1 = 4 и числе опытов N = 27). Таким образом, опыты можно признать воспроизводимыми.

Изначально регрессионная модель получена в следующем виде:

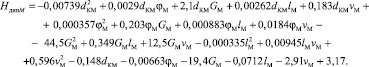(2)

Далее были рассчитаны величины, необходимые для оценки значимости факторов, входящих в уравнение (2). После исключения факторов, которые на основании результатов расчета величин tp можно предполагать незначимыми, и повторного расчета коэффициентов модели, регрессионная зависимость была получена в следующем виде:

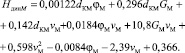(3)

Коэффициент детерминации R2 полученной регрессионной модели составляет 0,9660, что говорит о высокой сходимости расчетных, получаемых с использованием модели (3), и экспериментальных данных. Дисперсия адекватности разработанной модели составляет 1,3962 (при числе степеней свободы 17), дисперсия воспроизводимости принимает значение 0,9960 (при числе степеней свободы 26). Таким образом, расчетное значение критерия Фишера Fр = 1,4018, что меньше табличного значения FT = 2,0340 [4]. Таким образом, полученную модель можно признать адекватной.

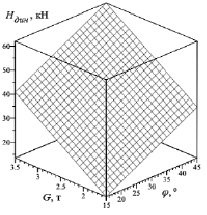
Рис. 1. Максимальное динамическое усилие в зависимости от угла наклона несущего каната и массы лесоматериалов

С учетом соотношений для параметров модели и натуры получим следующую регрессионную модель для расчета динамического усилия Hдин (кН) в зависимости от диаметра несущего каната dK (мм), угла наклона несущего каната φ (град), массы пачки лесоматериалов G (т) и скорости её транспортировки v (м/c) в натурной установке для транспортировки древесины:

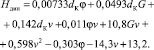(4)

Графически зависимость динамического усилия Hдин (кН) от различных параметров представлена на рис. 1–4.

Сплошная линия на графике представляет значения исследуемых величин, рассчитанные с помощью регрессионных моделей, маркеры – значения, рассчитанные с помощью теоретических зависимостей.

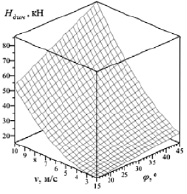
Рис. 2. Максимальное динамическое усилие в зависимости от угла наклона несущего каната и скорости перемещения

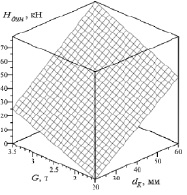
Рис. 3. Максимальное динамическое усилие в зависимости от диаметра несущего каната и массы лесоматериалов

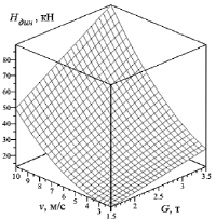
Рис. 4. Максимальное динамическое усилие в зависимости от массы лесоматериалов и скорости перемещения лесоматериалов

Далее проведена оценка сходимости результатов теоретических и экспериментальных исследований.

Заключение

Расчет коэффициентов детерминации теоретических значений относительно результатов, получаемых по экспериментальным зависимостям, показал достаточную степень сходимости теоретических и экспериментальных данных. При сопоставлении теоретических и экспериментальных значений максимального динамического усилия – R2 = 0,9326.

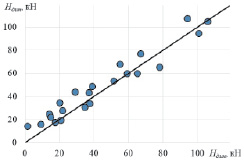
Рис. 5. Сопоставление теоретических и экспериментальных значений максимального динамического усилия

Рецензенты:

Иванов В.А., д.т.н., профессор, заведующий кафедрой воспроизводства и переработки лесных ресурсов, ФГБОУ ВПО «Братский государственный университет», г. Братск;

Гаспарян Г.Д., д.т.н., профессор, декан лесопромышленного факультета, ФГБОУ ВПО «Братский государственный университет», г. Братск.

Библиографическая ссылка