Современные системы управления промышленной автоматикой включают в себя сложные программно-аппаратные комплексы, состоящие из десятков и сотен компонентов: датчиков, исполнительных элементов, коммуникационных каналов, систем обработки информации и программных модулей. Дублирование функций аппаратных устройств достаточно хорошо изучено и описано в литературе [10, 3]. В критически важных узлах предусмотрено дублирование датчиков, исполнительных элементов, каналов передачи информации, серверов хранения и обработки информации, клиентских терминалов.
Производители устройств промышленной автоматики располагают обширной статистической информацией об отказах каждого вида устройств [15, 12]. Располагая подобной информацией, проектировщик имеет возможность оценить риски отказа той или иной подсистемы и спроектировать критически важные компоненты таким образом, чтобы применение наиболее надежных устройств в сочетании с дублированием и резервированием сводило риски к приемлемому уровню. В то же время сложные системы требуют разработки в своем составе программного комплекса управления технологическим процессом, который собственно и позволяет системе функционировать как единое целое, организуя взаимодействие ее компонентов в зависимости от условий окружающей среды и от хода технологического процесса. Отказы программного обеспечения, в том числе связанные с некорректной реализацией заложенных в систему управления математических моделей, могут приводить к отказу системы в целом, причем дублирование одинаковых копий программного обеспечения в этом случае ни в коей мере не устраняет проблему. В этой связи средством повышения надежности может стать мультиверсионное программирование.
Причины отказов и статистические данные о них
Производители устройств промышленной автоматики снабжают потребителей, которыми зачастую являются проектные и внедренческие предприятия, исчерпывающим методическим обеспечением [15, 12] по разработке соответствующего программного обеспечения. Но разработка программного обеспечения всегда сопряжена с риском возникновения ошибок на различных этапах. Ошибки на этапе составления программного кода, выявляемые компилятором, здесь несущественны, поскольку выявляются до ввода программного модуля в эксплуатацию. То же можно сказать о грубых логических ошибках в коде, всегда выявляемых на этапе тестирования системы. Наибольшее влияние на надежность программного комплекса оказывают ошибки, незначительные в обычных режимах работы, но проявляющиеся при выполнении нескольких условий. Как правило, программные модули тестируются на работоспособность в предельных режимах работы. В то же время ошибки могут проявляться при достижении предельных значений нескольких параметров одновременно.
Еще более «коварными» являются ошибки в сложных математических моделях, на основе которых построен программный код. Современные узлы промышленной автоматики работают под управлением программных модулей различной сложности. Единственный программный модуль может реализовывать как очень простую, так и чрезвычайно сложную логику управления исполнительными элементами в зависимости от показаний множества датчиков и накопленной информации. Рассмотрим, например, программный модуль, реализующий управление подсистемой распределительных камер аэротенков в системе управления городской канализацией (ПРКА ГК, рисунок). Соответственно, сложность программной реализации модулей чрезвычайно сильно различается. В состав изображенной подсистемы исполнительных механизмов подсистемы входят 8 регулирующих затворов, контрольно-измерительными приборами являются датчики уровня стоков и датчики положения затворов. Основной функцией алгоритма управления ПРКА является автоматическое позиционирование затворов в зависимости от задания перепада уровней стоков в распределительных камерах. Задача подсистемы – поддержание заданного перепада уровней в распределительных камерах посредством регулирования положения. Математическая модель расчёта расхода стоков, протекающих через затвор:
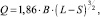
где B – ширина нижнего края затвора; L – уровень воды в распределительной камере; S – положение шибера (в мм). Значения L и S также оцениваются с использованием соответствующих математических моделей. Кроме того, для данного алгоритма задан комплекс условий разрешения работы. Сформированные задания поступают на регулятор положения, задачей которого является позиционирование шиберов.
Также программный модуль содержит обширное множество алгоритмов работы в нештатных ситуациях – при неисправности датчиков и исполнительных элементов.
Готовый программный модуль должен быть настроен. Далеко не полный перечень настраиваемых параметров приведен в таблице. Некорректный программный код любого из алгоритмов, реализованных в программном модуле, или некорректные значения параметров приводят к сбою в программном модуле и некорректной работе всей системы. Поскольку программный модуль, изображенный на рисунке, реализует вспомогательные функции системы, его отказ не приведет к немедленной аварии всей системы. В то же время, в той же рассматриваемой системе имеются чуть менее сложные модули, управляющие ее критически важными элементами. Отказ модуля может быть обнаружен соответствующими средствами мониторинга. В то же время, некорректная работа модуля (некорректная реализация математических моделей) приводит к работе системы в неоптимальном режиме, что приводит к быстрому износу, повышению риска аварийных ситуаций в иных частях системы, работающих в данном случае с повышенной нагрузкой, а в случае систем, подобных представленной на рисунке, к серьезным экологическим последствиям в среднесрочной перспективе. Обнаружение подобных неявных ошибок чрезвычайно затруднено.
В случае отказа программного модуля вследствие аппаратного сбоя средством повышения надежности системы, безусловно, является дублирование аппаратных ресурсов – датчиков, серверов, телекоммуникационных каналов. Нарушение же логики работы программы, не приводящее к ее остановке, будет повторяться на любом количестве ее копий.
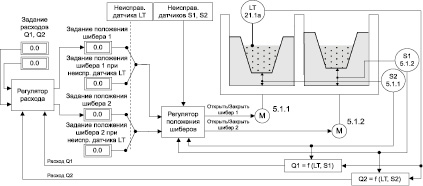
Структурная схема алгоритма управления ПРКА ГК (пример)
Параметры настройки алгоритма (пример)
|
Параметр |
Описание |
Значение |
|
Q1ном, Q2ном |
Номинальное значение задания расхода |
150 мм |
|
Q1 min, Q2 min |
Минимальное значение задания расхода |
50 мм |
|
Q1 max, Q2 max, |
Максимальное значение задания расхода |
1000 мм |
|
Тош.рег |
Задержка сообщения об ошибке регулирования |
120 с |
|
S1 безоп, …, S8 безоп |
Уставка безопасного положения затворов |
50 мм |
|
L1 авар. выс, L2 авар. выс |
Аварийно высокий уровень в распр. камере |
5800 мм |
|
L1авар.низк, L2 авар. низк |
Аварийно низкий уровень в распределительной камере |
900 мм |
|
Тзад.Lавар |
Задержка формирования сообщения об аварийном уровне в распределительной камере |
60 с |
Методы мультиверсионного программирования и оценки вероятности возникновения ошибок
Технология высоконадежного мультиверсионного программирования традиционно применяется в военной, в основном – космической [9, 8] сфере. Наземные комплексы управления космическими аппаратами комплектуются программным обеспечением, отдельные модули которого дублируют функции друг друга. Версии модуля разрабатываются независимыми командами программистов, раздельно тестируются. Кроме того, часто используются различные средства разработки. Версии исполняются параллельно, результаты работы каждой из них передаются вспомогательному модулю, осуществляющему сравнение результатов. Если результаты (в пределах установленной погрешности) совпадают, исполнительному элементу передается результат одного из модулей. В случае несовпадения, например, управляющее воздействие выбирается «большинством голосов» (требуется нечетное число версий модулей). В любом случае применение мультиверсий позволяет выявить наличие проблемы в программном коде. Выявленная ошибка в программном коде может служить сигналом к переводу системы в особый аварийный режим работы, к остановке производства и т.д., до выявления причины ошибки и ее устранения. Таким образом, во многих случаях системы промышленной автоматики не требуют наличия нечетного количества мультиверсий. Наличие хотя бы двух независимо разработанных версий позволяет в большинстве случаев выявлять ошибку.
Пусть вероятность возникновения ошибки в i-й версии программного модуля равна pi. Тогда вероятность одновременного возникновения ошибки во всех модулях равна
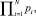
где N – число версий модуля, и вероятность обнаружения ошибки равна 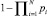 .
.
Очевидно, что данное значение стремится к 1 с ростом N. Поскольку программные модули проходят всестороннее тестирование, вероятность ошибки в каждой из версий модуля невелика. Например, если вероятность ошибки в каждой из двух версий модуля равна 0,001 %, вероятность одновременного возникновения ошибки сокращается до 0,0000001 %.
Для оценки предполагаемого числа ошибок используются разнообразные модели. Например, в [7] предлагается следующая оценка первоначального числа ошибок D0:
D0 = V/3000, (1)
где V – объем программы в бит информации. Объем, в свою очередь, оценивается как
V = N∙log2η,
где η = η1 + η2 – число уникальных операторов и операндов программы; N = N1 + N2 – число обращений к ним в ПО.
Число ошибок на m этапе тестирования модель Холстеда [13] оценивает как
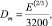 (2)
(2)
где E – оценка сложности системы:
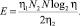
Данные модели сложности и предполагаемого числа ошибок могут быть использованы в качестве грубых оценок. Пусть для каждого из M модулей имеется несколько версий, Vj для j-го модуля. Пусть Pji – вероятность безотказной работы i-й версии j-го модуля. Если отказ любого из модулей ведет к отказу всей системы, то вероятность P безотказной работы системы может быть выражена следующим образом:
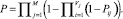
Оптимизационная модель надежности программного комплекса
В свою очередь, вероятность безотказной работы может быть оценена через число ошибок (1)–(2).
Сложность каждого из модулей можно считать приблизительно одинаковой вне зависимости от конкретной реализации. Таким образом, зная сложность единственной версии каждого модуля, может быть получена оценка вероятности безотказной работы системы в целом в зависимости от числа версий каждого из модулей и вероятности безотказной работы Pj единственной версии:
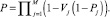
В то же время увеличение числа версий каждого из модулей сопряжено с увеличением стоимости системы. Для систем промышленной автоматики будем считать приемлемым число версий модуля, не превышающее 2. Введем булевы переменные xj, равные 1, если предполагается дублирование j-го модуля и константы Cj – стоимость разработки j-го модуля. Тогда при заданном бюджете C на разработку всего программного комплекса имеем оптимизации:
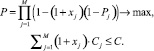 (3)
(3)
Задачи псевдобулевой оптимизации подобного («рюкзачного») типа исследованы в работах А.Н. Антамошкина [11, 1, 2] и др. Созданы методы [5, 14], позволяющие получать субоптимальное (достаточно точное) решение подобных задач размерности до миллионов переменных, что позволяет решать задачи, подобные (3). Для задач с монотонной целевой функцией могут быть также успешно применены жадные эвристики [4] или специальные агломеративные жадные эвристики [6].
Заключение
Задача повышения надежности систем промышленной автоматики кроме дублирования функций аппаратных устройств требует в некоторых случаях дублирования также и программных модулей. Задача построения оптимальной конфигурации требуемых программных модулей может быть сведена к задаче псевдобулевой оптимизации.
Рецензенты:
Антамошкин А.Н., д.т.н., профессор, зав. кафедрой математического моделирования и информатики, ФГБОУ ВПО «Красноярский государственный аграрный университет», г. Красноярск;
Ступина А.А., д.т.н., профессор, зав. кафедрой «Экономика и информационные технологии менеджмента», ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Библиографическая ссылка
Сташков Д.В., Насыров И.Р., Казаковцев Л.А., Казаковцев Л.А. ЗАДАЧА ФОРМИРОВАНИЯ ОТКАЗОУСТОЙЧИВОГО ПРОГРАММНОГО КОМПЛЕКСА УПРАВЛЕНИЯ ПРОМЫШЛЕННЫМ ОБЪЕКТОМ // Фундаментальные исследования. 2015. № 5-1. С. 149-153;URL: https://fundamental-research.ru/ru/article/view?id=38024 (дата обращения: 06.02.2026).



