Циклические разбиения
При переходе в радиосхемах с макро- на микро-, а затем на наноуровень модель кольца приобретает все более важное значение. На макроуровне любую электрическую цепь (со времен Кирхгоффа) и простую радиосхему для необходимых расчетов принято заменять модельной системой сопряженных замкнутых цепей, циклов (колец) и рассчитывать, исследовать или реально собирать циклы в отдельности. Теоретически каждая фиксированная «цветная» точка кольца может определять функцию элемента кольца (резистора, конденсатора, источника, выпрямителя, транзистора и др.) или соответствовать материалу (проводнику, диэлектрику и пр.). Анализ и компьютерное моделирование колец и их наноструктурных элементов составляет цель данной работы.
Комбинаторные методы перечисления циклических разбиений (колец)
На первом этапе исследований колец возникла задача перечисления циклических разбиений с заданным количеством точек двух сортов (двуцветные разбиения): занятых и не занятых атомами позиций в структуре цикла, названных циклотомическими наборами точек. Исследования, проведенные в рентгеновском структурном анализе (РСА) кристаллов Паттерсоном, Хоземаном и Бахчи, Бюргером и др., завершились работой [5] по перечислению «двухцветных» целочисленных циклических разбиений. Кратко представим полученные результаты.
Для перечисления разбиений 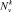 заданного периода v, содержащего k – занятых позиций точек, использовались комбинаторные методы теории чисел [10]. Было показано (теорема 1 в [5]), что каждой блок-схеме с автоморфизмом α:aij + 1 → ai + 1,j; Bi,k → Bi + 1,k , переставляющим как элементы aij, так и блоки Bi,k блок-схемы по циклу длины v, соответствует один и только один циклотомический набор, а поэтому число блок-схем из множества Е = {0, 1, …, v – 1} с │Е│ = v равно количеству циклических разбиений
заданного периода v, содержащего k – занятых позиций точек, использовались комбинаторные методы теории чисел [10]. Было показано (теорема 1 в [5]), что каждой блок-схеме с автоморфизмом α:aij + 1 → ai + 1,j; Bi,k → Bi + 1,k , переставляющим как элементы aij, так и блоки Bi,k блок-схемы по циклу длины v, соответствует один и только один циклотомический набор, а поэтому число блок-схем из множества Е = {0, 1, …, v – 1} с │Е│ = v равно количеству циклических разбиений 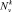 . После преобразований получено
. После преобразований получено
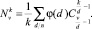
Во всех этих работах конкретные структуры колец были представлены не достаточно полно. Классификация и анализ структур цветных колец, в которых точками являются модели нанокластеров, явились целью проведения исследований, представленных в данной работе.
Компьютерный перебор структур цветных колец на основе групп подстановок
На начальном этапе исследований цветных колец, как и в случае с циклотомическими двухцветными наборами точек, предлагается способ расчета структур многоцветных циклических разбиений и их классификация на основе симметрии групп подстановок. Из теории групп [7] известно, что N! перестановок N чисел составляет их наибольшее количество и принадлежит полной группе симметрии перестановок чисел. Полная группа разбивается на подгруппы порядка р. Элемент подгруппы перестановки будет соответствовать определенной структуре кольца, если каждому числу на кольце однозначно поставить в соответствие число в перестановке. В то же время каждой перестановке соответствует собственная внутренняя структура, которую можно представить в виде произведения подциклов.
Считая точки, принадлежащие одному подциклу, идентичными, то есть имеющими один и тот же цвет, получаем разбиение перестановки на цветные подциклы. Каждая подгруппа, содержащая р элементов (порядок группы), определяет количество структур колец с общей симметрией этой группы. Таким образом, получаем возможность для классификации структур колец по их принадлежности к одной подгруппе, а цветные подциклы в подстановке позволяют определять структуру цветного кольца. Для вывода преобразований симметрии подгруппы подстановок и построения групповой таблицы Кэли была составлена программа перемножения элементов группы. Произведение матриц перестановок в программе реализуется по правилу: «левая» подстановка умножается на «правую». В качестве примера может служить операция произведения двух подстановок с числом элементов N = 8 следующим образом:

Таблица 1
Таблица Кэли для подгруппы подстановок с N = 8
g[0] = (0 1 2 3 4 5 6 7); g[0] g[1] g[2] g[3] g[4] g[5] g[6] g[7]
g[1] = (4 5 6 7 1 0 3 2); g[1] g[2] g[3] g[0] g[5] g[6] g[7] g[4]
g[2] = (1 0 3 2 5 4 7 6); g[2] g[3] g[0] g[1] g[6] g[7] g[4] g[5]
g[3] = (5 4 7 6 0 1 2 3); g[3] g[0] g[1] g[2] g[7] g[4] g[5] g[6]
g[4] = (6 7 5 4 2 3 1 0); g[4] g[7] g[6] g[5] g[2] g[1] g[0] g[3]
g[5] = (2 3 1 0 7 6 4 5); g[5] g[4] g[7] g[6] g[3] g[2] g[1] g[0]
g[6] = (7 6 4 5 3 2 0 1); g[6] g[5] g[4] g[7] g[0] g[3] g[2] g[1]
g[7] = (3 2 0 1 6 7 5 4); g[7] g[6] g[5] g[4] g[1] g[0] g[3] g[2]
В соответствии с теоремами, доказательство которых приведено в учебной литературе по теории групп, разбиение подстановки на замкнутые подциклы можно произвести так, как это показано для левой матрицы в приведенном выше равенстве. Действительно, 0 → 5 → 1 → 4 → 0, и 2 → 7 → 3 → 6 → 2. Образуется два подцикла, и подстановка дает следующий результат: (54760123) = (0514)(2736). Поскольку операция перестановки разбилась на два подцикла, можем считать её двухцветной. В программе выбираются перестановки, которые принадлежат одной подгруппе, а затем автоматически составляется соответствующая таблица умножения группы – таблица Кэли (табл. 1).
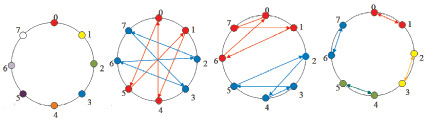
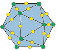
а б в г
Рис. 1. Элементы подгруппы подстановок кольца (выделены трансляционно не эквивалентные цветные кольца – «ожерелья» из таблицы Кэли (табл. 1): а – 01234567 = (0)(1)(2)(3)(4)(5)(6)(7) – восьмицветное преобразование; б – 54760123 = (0514)(2736) – двухцветное преобразование; в – 76453201 = (0716)(2435) – двухцветное преобразование; г – 10325476 = (01)(23)(45)(67) – четырехцветное преобразование
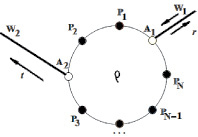
Рис. 2. Кольцо Ааронова – Бома с двумя присоединенными проводниками и примесями на кольце (Aj – точки соединения проводников с кольцом, Pi – точки нахождения примесей Wj – проводники
Добавление к подгруппе операции подстановки, не принадлежащей этой подгруппе, приводит к расширению подгруппы. В программе предусмотрено также графическое представление («визуализация») структуры каждой подстановки в модели периодического разбиения двумерного пространства. По теореме об изоморфизме конечных групп симметрии и групп перестановок «визуализировать» можно любую абстрактную конечную группу, зная вид ее таблицы Кэли, что было ранее продемонстрировано в работе [8]. Циклическое одномерное разбиение позволяет предложить еще один более простой, но не менее важный в приложениях способ «визуализации» подгруппы (рис. 1).
Квантовое кольцо [1]
На микроуровне электронному транспорту в квантовых кольцах при наличии точечных рассеивающих центров, в качестве которых могут выступать одиночные примеси или наномерные «квантовые точки», посвящено много работ. Так, например, в работе [1] рассмотрена система, состоящая из кольца Ааронова – Бома радиуса ρ с прикрепленными к нему одномерными проводниками W1 и W2 (рис. 2).
Точки контактов между проводниками и кольцом обозначены A1 и A2. Рассмотрен случай, когда на кольце имеется N короткодействующих рассеивающих центров. Проводники моделируются положительными полуосями х ≥ 0.
Кольцо помещено в магнитное поле В, перпендикулярное плоскости кольца. В системе реализуется одномодовый режим электронного транспорта и все транспортные характеристики системы определяются единственным коэффициентом прохождения электрона (кондактансом). В работе получены аналитические выражения для коэффициента прохождения и исследована зависимость электронного транспорта от энергии электронов, от величины внешнего магнитного поля и от положения примесей. В этой задаче представлен частный случай цветного кольца, у которого структура и свойства определены симметрией распределения «нагруженных» точек и ее нарушениями (преобразованиями).
Проблема контактов в наноструктурной системе и кластерные элементы кольца
Нарушения транспорта электронов могут существенно сказываться на работе электронных устройств, собранных на наноуровне. Причины, приводящие к нарушению стабильности работы устройств, можно в этом случае классифицировать на «внешние» и «внутренние». Внутренние причины связаны, в первую очередь, с возможностью получения бездефектных проводников и квантовых точек (нанокластеров), а затем с технологией сборки в местах контактов, то есть с такой же проблемой, с которой столкнулась в начале своего развития микроэлектроника (нобелевская лекция Ж.И. Алферова). Действительно, и квантовая точка в кольце, и проводник на наноуровне представляют собой наноструктуры, и каким образом кластер будет контактировать с мифической полуплоскостью проводника, с точки зрения технологии не совсем понятно. И квантовая точка при сборке цветного кольца, и проводник в этом случае представляют собой наноразмерные кластеры, а их геометрия (расположение и координации атомов в различных плоскостях) будет существенно влиять на транспортные свойства электронов.
В любом случае необходим априорный компьютерный эксперимент, определяющий – хотя бы на уровне геометрии, но близкий к реальным условиям – результат взаимодействия наноструктур при их контакте. С этой целью на основе расширения разработанной ранее авторами [5] компьютерной программы создана новая программа, имитирующая процесс сборки реальных (или модельных) нанокластеров определенного состава в рамках одно- или многоцентровой задачи зарождения структур. В многоцентровой задаче предусмотрено три варианта расчета: первый: НП – однокомпонентный со случайной ориентацией центров зарождения в случайные моменты времени начала роста, второй: НП – однокомпонентный с фиксированной ориентацией центров зарождения и третий: НП – многокомпонентный (гетерофазный) со случайной ориентацией центров зарождения в случайные моменты времени.
Сложность проектирования конкретных схем и их сборки на технологическом уровне связана с отсутствием сколько-нибудь полного банка структур не только реальных, но и модельных нанокластеров. Результаты применения нами методики моделирования отдельных нанокластеров на основе информации баз данных РСА позволили рассчитать структуры отдельных нанокластеров, которые представлены в табл. 2.
Таблица 2
Нанокластеры, рассчитанные на основе информации баз данных РСА
|
№ п/п |
Химсостав (формульные единицы); пространственная группа симметрии |
Кластерная геометрическая модель |
Последовательность чисел заполнения k-й поверхности кластера «магические числа») |
Публикация |
|
1 |
2 |
3 |
4 |
5 |
|
1. |
Галит (поваренная соль) 1. (NaCl)2 – димер. 2. (NaCl) – диполь пр. гр. Fm3m |
1 2 |
Куб (гексаэдр) 6k2 + 2; Октаэдр 4k2 + 2 (РСА) |
[9] |
|
3. |
Теллурид свинца PbTе, (PbTе)2 пр. гр. Fm3m |
|
Куб (гексаэдр) 6k2 + 2, или кубоокта – эдр10k2 + 2 (РСА.ЭМ) |
[3] |
|
1. Металлическая медь Cu, Ag и др. пр. гр. Fm3m, 2. Магний Mg2 пр. гр. P6(3)mmc |
1 2 |
1. Кубооктаэдр 10k2 + 2. 2. Гексагональная призма18k2 + 2 (РСА) |
Не опубликовано |
|
|
Сера молекулярная S8 пр.гр. P2/c |
|
«Скошенная» дипирамида (РСА) 14 k2 – 2 |
[6] |
|
|
Окись алюминия
пр. гр. |
|
«Скрученная» тригональная призма (РСА) 4k2 + 2 |
[4] |
|
|
6. |
Цинк, магний, кадмий, окись цинка пр.гр. P6(3)mmc; |
|
Либо «скошенная» гексагональная дипирамида (РСА, ЭМ): 1, 12, 44, 96, 170, 264, ... либо икосаэдр либо кубооктаэдр (масс-спектр Mg): 10k2 + 2. |
[3] |
|
7. |
Антрацен пр.гр. P21/a |
|
Вытянутый кубооктаэдр: 10k2 + 2 (РСА) |
[4] |
|
9. |
Декакарбамид нитрата кобальта
пр. гр. |
|
Искаженная гексагональная дипирамида 6k2 + 2 (РСА) |
[9] |
|
10. |
Тетракарбамид нитрата кобальта пр. гр. Р 21/с |
|
4к2 + 2:6,38,102,. 8k2 + 2:10,34,74,. (РСА) |
[9] |
|
11. |
Йод молекулярный I2 пр. гр. B mab |
|
Вытянутый кубооктаэдр 10k2 + 2 (РСА) |
[3] |
|
12 |
Индий пр.гр. P4(2)nnm |
|
Вытянутый кубооктаэдр 10k2 + 2 (РСА) |
[3] |
|
Натрий пр.гр. I m3m |
|
Ромбододекаэдр или октаэдр 12k2 + 2 (РСА) |
[3] |


а б
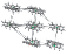
Рис. 3. а – нанокластеры оксида цинка (размерами около 500нм) в электронной микроскопии [Zhong Lin Wang // J. Phys. Condens. Matter. 2004, 16, R829-R858.]; б – рассчитанные в программе моделирования многоцентровой задачи зарождения кластеров ZnO (ранее не опубликовано)
К сожалению, прямых экспериментальных доказательств существования нанокластеров, модели которых приведены в табл. 2, пока существует мало. В качестве одного из примеров приведем фотографию реального эксперимента по веществу оксида цинка, полученную методами электронной микроскопии (рис. 3, а) и модельное изображение нанополикристалла (рис. 3, б), полученное по результатам компьютерного эксперимента в программе моделирования многоцентровой задачи зарождения кластеров.
Выводы
Внешние причины нарушения работы электронных устройств достаточно подробно рассмотрены нами ранее в работе [3]. Сюда в первую очередь относятся изменения свойств и структуры нанокластеров под влиянием всех видов космического излучения. Исходя из выводов, сделанных в рассмотренной выше теоретической работе [1], следует добавить к выводам, сделанным в статье [3], негативную возможность воздействия сильных магнитных полей на транспорт электронов в нанокластерных системах колец.
Работа поддержана грантом РФФИ № 14-02-97504.
Рецензенты:
Полушин П.А., д.т.н., профессор, ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Владимир;
Легаев В.П., д.т.н., профессор, заведующий кафедрой приборостроения и информационно-измерительных технологий, ФГБОУ ВПО «Владимирский государственный университет имени А.Г. и Н.Г. Столетовых», г. Владимир.
Библиографическая ссылка
Рау В.Г., Никитин О.Р., Рау Т.Ф., Ломтев Л.А., Горшков К.А. НАНОКЛАСТЕРНЫЕ СИСТЕМЫ КОЛЕЦ ДЛЯ ЭЛЕКТРОНИКИ // Фундаментальные исследования. 2015. № 5-1. С. 137-142;URL: https://fundamental-research.ru/ru/article/view?id=38022 (дата обращения: 03.03.2026).















 .
.