Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Габрюк В.И. 1

---

1 Дальневосточный государственный бюджетный технический рыбохозяйственный университет

Аналитически исследуются крючковые рыболовные системы: удочки, троллы и ярусы. Получено общее аналитическое решение дифференциальных уравнений равновесия гибкого каната в покоящейся жидкости, являющееся обобщением работы И. Бернулли на случай, когда канат (хребтина крючкового яруса) легче воды. Это решение позволяет выполнять математическое моделирование любых крючковых рыболовных систем в покоящейся жидкости. Для дрейфующих крючковых ярусов и стационарных ярусов при наличии течений разработаны математические модели их элементов: рыболовного крючка, крючкового поводца, системы «наживка – крючок – поводец», узла крепления поводца к хребтине; гибкого каната в потоке; хребтины, якоря. На основе этих математических моделей на языке программирования Borland Delphi разработан программный комплекс CM-LongLine, позволяющий выполнять компьютерное моделирование всех типов ярусов при наличии течений. С разработкой математических моделей рыболовных систем промышленное рыболовство поднимается от ремесла, каким оно было до сих пор, до уровня точной науки, опирающейся на прочный фундамент математики, механики, физики, информатики и логики. Полученные в данной работе адекватные математические модели и компьютерные программы могут быть положены в основу новой науки «Математическое промышленное рыболовство на персональном компьютере».

Статья в формате PDF

2695 KB

рыболовный крючок

крючковый поводец

хребтина яруса

якорь

адекватные математические модели

компьютерное моделирование ярусов

1. Аппель П. Теоретическая механика. – М.: Гос. изд-во физ.-мат. литературы, 1960. – т. 1. – 516 с., т. 2. – 488 с.

2. Габрюк В.И., Кулагин В.Д. Механика орудий рыболовства и АРМ промысловика. – М.: Колос, 2000. – 416 с.

3. Габрюк В.И., Чернецов В.В., Бойцов А.Н. Основы моделирования рыболовных систем. – Владивосток: Дальрыбвтуз, 2008. – 560 с.

4. Габрюк В.И. Методы проектирования и моделирования рыболовных орудий. – Владивосток: Дальрыбвтуз, 2014. – 432 с.

5. Зарубин В.С. Математическое моделирование в технике. М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. – 495 с.

6. Киттел Ч., Найт В., Рудерман М. Механика. Берклеевский курс физики (Том 1). – М.: Наука, 1983. – 448 с.

7. Кокорин Н.В. Лов рыбы ярусами. – М.: ВНИРО, 1994. – 421 с.

8. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – М.: Физматгиз, 2002. – 320 с.

9. Седов Л.И. Механика сплошной среды. – М.: Наука, 1973. т.1, 536 с. – т.2, 584 с.

10. Bernoulli J. Solutio problematis funicularii. – Acta eruditorum, Lipsiae, 1691. June. P. 262–276.

Математическое моделирование в технике [3–9] является важнейшим инструментом познания реального Мира. Под математическим моделированием понимают замену исследуемого технического устройства математической моделью и его изучение методами вычислительной математики с использованием современной компьютерной техники.

Объектом исследования являются крючковые рыболовные системы: удочки, троллы и ярусы. Основными крючковыми орудиями рыболовства являются пелагические, донные и придонные горизонтальные ярусы (рис. 1), которые широко используются для лова таких рыб, как тунец, акула, меч-рыба, треска, чёрный палтус, окунь, терпуг, угольная рыба.

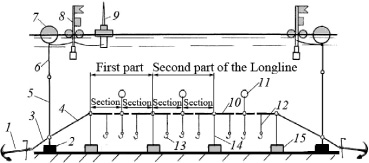
Рис. 1. Горизонтальный придонный ярус: 1 – якорь; 2 – подъякорник; 3 – якорный трос; 4 – якорный линь; 5 – плавучий линь; 6 – линь якорного буя; 7 – якорный буй; 8 – буй-веха; 9 – радиобуй; 10 – хребтина; 11 – поплавок; 12 – поводец; 13 – рыболовный крючок; 14 – грузовой линь; 15 – груз

Ярус представляет собой длинный канат (хребтину), к которому на определённом расстоянии друг от друга крепятся поводцы с рыболовными крючками. Ярус набирается из отдельных секций. Секция яруса (section of the longline) – это отрезок хребтины с огонами на концах. В секции яруса размещается от шести для тунцеловных ярусов до 300 крючков при лове трески и палтуса. Ярусы отличает простота конструкции, высокое качество улова, способность облавливать гидробионты на любых глубинах и при наличии сложных грунтов, когда иные орудия использовать невозможно.

Целью исследования является получение математических моделей элементов крючковых орудий рыболовства (рыболовного крючка, крючкового поводца, узла крепления поводца к хребтине, системы «рыболовный крючок – наживка – поводец»; гибкого каната как в потоке, так и в покоящейся жидкости; хребтины яруса, якорей с подъякорниками и без них), необходимых для математического моделирования крючковых рыболовных систем: удочек, троллов; горизонтальных, вертикальных и комбинированных крючковых ярусов как стационарных, так и дрейфующих.

Материалы и методы исследования

Математическая модель гибкого каната в потоке

Гибкий канат является основным элементом любых крючковых рыболовных систем, поэтому его математическая модель лежит в основе их моделирования. Векторное дифференциальное уравнение равновесия гибкого каната в потоке имеет вид [1–3]

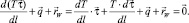(1)

Здесь T – натяжение каната в текущей точке; – орт касательной оси каната, направленный в сторону роста дуговых координат l; 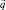– вес в воде 1 м каната; 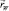– гидродинамическая сила, приходящаяся на 1 м каната.

Скалярные дифференциальные уравнения равновесия каната получаются путём проецирования векторного уравнения (1) на оси какой-либо системы координат. Канаты орудий рыболовства работают в воде, поэтому при их исследовании используется три системы координат: земная 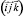, естественная 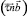и поточная .

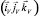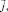
Земная система координат (ЗСК) задаётся векторами . Вектор направлен по отвесу, то есть ( – ускорение свободного падения). Векторы лежат в плоскости горизонта. Эта система используется для задания положения каната относительно Земли и определения его формы. Форма каната задается выражением

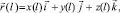
где ; х, у, z; l – радиус-вектор, декартовы и дуговая координаты текущей точки оси каната.

Естественная система координат (ЕСК) каната задаётся векторами , , :

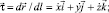
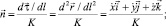
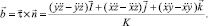
Здесь , , – орты касательной, главной нормали и бинормали оси каната; 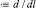– символ производной по дуговой координате; 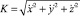– кривизна оси каната.

Поточная система координат каната (ПСК) задаётся векторами :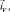

, .

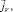
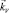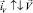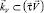Здесь 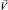– скорость потока. Эта система используется при определении гидродинамических сил, действующих на канат в потоке.

Если скорость потока 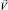лежит в плоскости горизонта, то ось абсцисс земной системы координат x направляют по оси xV, рис. 2. В этом случае ориентация поточной системы координат относительно земной определяется углом φ между осями z и zV, называемым углом крена плоскости потока каната .

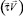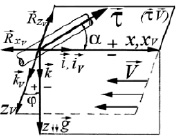
Рис. 2. Земная xyz и поточная xVyVzV системы координат каната: 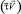– плоскость потока каната; α – угол атаки каната; φ – угол крена плоскости потока каната

Проецируя векторное уравнение (1) на оси поточной системы и учитывая, что

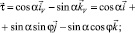
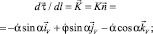
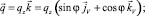
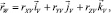
после преобразований, получим

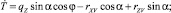
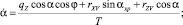
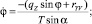(2)

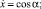
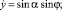
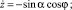
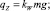
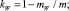
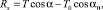
где T0, α0; T, α – натяжение каната и его угол атаки в начальной и текущей точках; qz – проекция веса в воде 1 м каната на ось 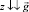; mW, m – масса воды, вытесненной 1 м каната и его линейная плотность; rXV, rYV, rZV – проекции гидродинамической силы каната на оси поточной системы координат; Rx – гидродинамическое сопротивление каната.

Система дифференциальных уравнений (2) является математической моделью каната в потоке. Она позволяет находить семь функций: x(l), y(l), z(l), T(l), Rx(l), α(l), φ(l), определяющих форму каната в потоке x(l), y(l), z(l), его натяжение T(l) и гидродинамическое сопротивление Rx(l), а также его угол атаки α(l) и угол крена плоскости потока φ(l). Эта система записана в нормальной форме, наиболее удобной для её численного решения на ЭВМ.

Проекции гидродинамической силы каната на оси поточной системы координат

rXV, rYV, rZV, входящие в (2), зависят от его угла атаки α и определяются экспериментально путём испытания канатов в аэродинамических трубах, гидролотках или в море. Их обычно записывают в форме Ньютона:

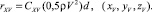
Здесь d – диаметр каната; CXV, CYV, CZV – коэффициенты гидродинамических сил. Эти коэффициенты удовлетворяют следующим условиям симметрии:

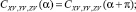
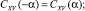
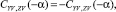
то есть они являются периодическими функциями угла атаки α с периодом π, причём CXV(α) – чётная функция, а CYV,ZV(α) – нечётные функции. Они также удовлетворяют граничным условиям:

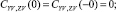
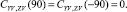
Условиям симметрии и граничным условиям удовлетворяют следующие функции:

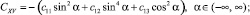
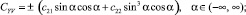
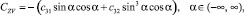
где cij – коэффициенты, зависящие от материала каната, числа наружных прядей, отношения длины каната к его диаметру l/d (при l/d > 100 канат можно рассматривать как канат бесконечного удлинения). Знак (+) во второй из формул относится к канатам правой свивки наружных прядей, знак (–) – канатам левой свивки.

Для получения дифференциальных уравнений равновесия каната в естественных осях умножим уравнение (1) скалярно на 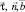, получим

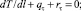
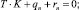
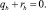
Здесь

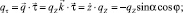
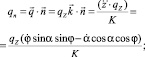
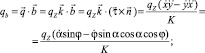
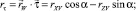
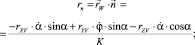
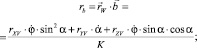
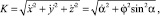
где К – кривизна оси каната; qτ, qn, qb, rτ, rn, rb – проекции веса 1 м каната в воде и гидродинамической силы, приходящейся на 1 м каната, на естественные оси.

Для моделирования стационарных ярусных систем в покоящейся жидкости рассмотрим равновесие каната в покоящейся жидкости. Эта задача решена И. Бернулли [10] для случая, когда плотность материала каната больше плотности жидкости.

Равновесие канатов в покоящейся жидкости описывается векторным дифференциальным уравнением, получаемым из (1) при :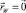

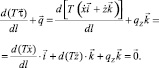(3)

Так как силы 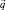параллельны оси z, то канат лежит в плоскости (xz), поэтому y ≡ 0. Проецируя уравнение (3) на оси х и z земной системы координат, получим дифференциальные уравнения равновесия гибкого каната в покоящейся жидкости:

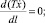
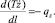(4)

Общее решение системы (4) имеет вид:

при qz ≠ 0:

;

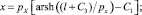
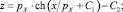
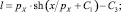
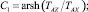
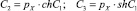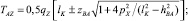
(+) – при qz > 0, (–) – при qz < 0; (5)

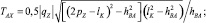
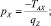
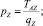
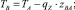
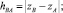
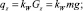
при qz = 0: T = C4 = const; z = C5x + C6,

где mW – масса воды, вытесненной 1 м каната; m – линейная плотность каната; qz – проекция на ось z веса в воде 1 м каната; kW – коэффициент веса каната в воде; l – дуговая координата текущей точки каната; lk – длина каната; C1, ..., C6 – константы интегрирования; zA, zB – аппликаты начальной и конечной точек каната; pX, pZ – параметры каната; TAX, TAZ – проекции натяжения каната в начальной точке А на оси x и z, рис. 3.

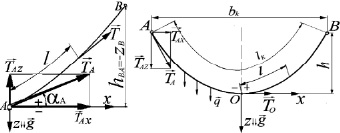
а б

Рис. 3. Параметры: а – несимметричного каната; б – симметричного каната

Система (5) является развитием работы [10] на случай, когда канат может быть как тяжелее воды (сталь, полиамид, полиэстер), так и легче воды (полиэтилен, полипропилен, дэнлайн).

При получении уравнений (5) использовалась система координат xz, ось z которой направлена по ускорению свободного падения, т.е. 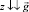. Кроме того, дифференциал дуговой координаты определялся по формуле 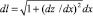, где перед радикалом взят знак (+). Она верна только тогда, когда дифференциалы дуговой координаты dl и абсциссы dx имеют одинаковые знаки. Поэтому ось x необходимо направлять в ту сторону, чтобы с ростом дуговых координат росли и абсциссы, как показано на рис. 3. Это обстоятельство необходимо учитывать при решении конкретных задач.

Система (5) является общей математической моделью однородного неподвижного гибкого каната в покоящейся жидкости. Она позволяет определять характеристики любых канатов в покоящейся воде, изготовленных из материалов как тяжелее воды, когда qz > 0 (сталь kW = 0,87; капрон kW = 0,1; полиэстер kW = 0,126), так и легче воды, когда qz < 0 (полиэтилен kW = –0,068; полипропилен kW = –0,126). Математическая модель (5) лежит в основе математического моделирования любых крючковых рыболовных систем в покоящейся жидкости.

Для симметричного каната, когда оси координат выбраны так, как показано на рис. 3, б, выполняются условия: zA = zB, С1 = С3 = 0, С2 = pX и формулы (5) принимают вид

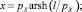
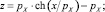(6)

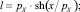
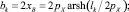
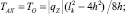
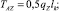
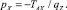
Здесь bk – хорда каната; lk – длина каната; h – стрелка прогиба (рис. 3).

Уравнения (6) являются математической моделью симметричного каната в покоящейся жидкости.

Математическая модель рыболовного крючка

Рыболовный крючок служит для размещения наживки, захвата и удержания рыбы. В настоящее время используются плоские и пространственные крючки. Пространственный крючок работает на растяжение, изгиб и кручение. Так как напряжения от растяжения и кручения малы (они не превышают 2 % напряжений изгиба), то диаметр проволоки крючка определяется из условия его прочности на изгиб.

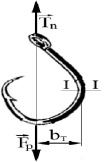
Рис. 4. Силы, приложенные к рыболовному крючку: Fp – сила, с которой рыба действует на крючок; Tn – натяжение поводца; bT – плечо натяжения поводца

Условие прочности рыболовного крючка заключается в том, что максимальное напряжение в наиболее нагруженном сечении крючка (сечение I–I, рис. 4) должно быть меньше допускаемого:

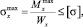
где – максимальный изгибающий момент; Tn – натяжение поводца, при котором разрушается ротовая полость рыбы (определяется по формуле Tn = kpGp); kp – коэффициент прочности ротовой полости рыбы, определяемый экспериментально (для трески kp = 1,5–3,0; меньшие значения – для более крупных рыб); Gp – вес рыбы в воздухе; 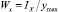– момент сопротивления поперечного сечения крючка; 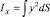– момент инерции поперечного сечения крючка.

Для крючка, поперечное сечение которого – круг диаметром d, имеем

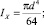
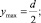
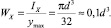
Крючки в основном выполняются из проволоки круглого сечения. В этом случае условие прочности крючка имеет вид

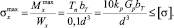
Откуда находим диаметр проволоки рыболовного крючка:

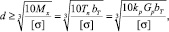(7)

где 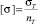– допускаемое напряжение для материала крючка; σT – предел текучести материала крючка; nT – коэффициент запаса прочности по текучести.

Максимальное натяжение крючкового поводца , при котором рыболовный крючок разгибается, определяется по формуле

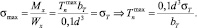
Разрывное усилие крючкового поводца:

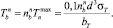(8)

Здесь 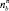– коэффициент запаса поводца на разрыв 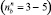. Диаметр нитки крючкового поводца выбирается по таблицам ГОСТ по его разрывному усилию .

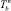Математическая модель системы «наживка – крючок – поводец»

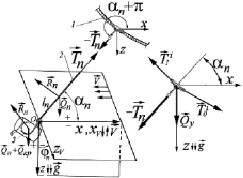
Характеристики крючкового поводца: натяжение Tn, угол атаки αn, угол крена плоскости потока φn, необходимые для моделирования хребтин ярусов, определяются из условий равновесия системы «наживка – крючок – поводец» (рис. 5).

Векторное уравнение равновесия системы «наживка – крючок – поводец» имеет вид

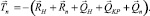
Проецируя это уравнение на оси земной системы координат, получим проекции натяжения поводца 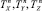на оси земной системы координат:

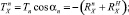(9)

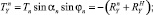
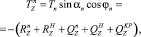
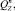
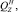
где Tn, αn – натяжение и угол атаки крючкового поводца; φn – угол крена плоскости потока поводца; 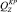– веса в воде поводца, наживки и крючка соответственно; 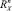, , 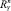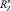– проекции гидродинамической силы поводца на оси земной системы координат, определяемые по формулам

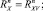
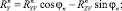
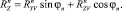(10)

Здесь

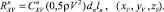
Из уравнений (9) и (10) следует:

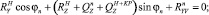(11)

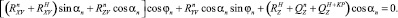
Система (10) – это система линейных алгебраических уравнений относительно sinφn и cosφn. По формулам Крамера находим

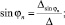
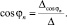
Угол атаки поводца αn определяется из соотношения

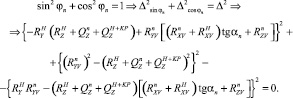(12)

а б

Рис. 5. Система «наживка – крючок – поводец»: 1 – хребтина; 2 – крючковый поводец; 3 – рыболовный крючок; 4 – наживка (а); б – узел крепления крючкового поводца к хребтине яруса

Угол крена плоскости потока поводца φn и его натяжение Tn определяются из соотношений

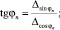
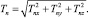(13)

Формулы (11)–(13) получены при допущении, что поводец является прямолинейным.

Математическая модель хребтины яруса с учетом течений

Система (2) лежит в основе моделирования хребтин ярусов с учётом течений. При разработке математической модели хребтины яруса необходимо учитывать действие на неё крючковых поводцов. Его можно учитывать двояко:

● во-первых, сосредоточенными силами (натяжениями поводцов Tn), приложенными в точках крепления поводцов к хребтине;

● во-вторых, путём равномерного распределения натяжения поводцов по длине хребтины.

В первой методике хребтина на i-м участке рассматривается состоящей из 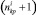отрезков, на которые она делится точками крепления к ней крючковых поводцов. Здесь 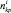– количество крючков на i-м участке. В этом случае каждый отрезок хребтины нагружен весом в воде и гидродинамическими силами. Характеристики хребтины на i-м участке определяются путем численного решения задачи Коши для уравнений равновесия хребтины в потоке (2) на каждом из 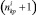ее отрезков. Начальные данные T0, α0, φ0 для решения задачи Коши определяются из условий равновесия узлов крепления поводцов к хребтине (рис. 5, б):

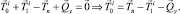
Проецируя это уравнение на оси земной системы координат, получим

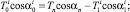(14)

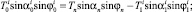
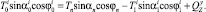
Здесь 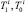– натяжения хребтины до и после i-го узла крепления поводца к хребтине (рис. 5, б); 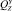– вес в воде узла соединения поводца с хребтиной;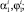 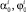– углы атаки хребтины и крена плоскости потока до узла и после него.

Для расчета характеристик хребтины на i-м участке необходимо определять 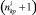раз начальные данные, а именно: в начале участка (точке Ai) и в точках крепления поводцов к хребтине Ki1, Ki2, Ki3, ... (рис. 6).

Первая методика удобна при расчёте ярусов для лова тунцов, когда на участке длиной 300 м размещается 5–6 поводцов с крючками, расстояние между которыми 30–60 м. Но она сложна при расчёте придонных ярусов, когда на участке яруса размещается много крючков (250 и более) при расстоянии между крючками 1,0–1,5 м. В этом случае расчёты удобнее вести по второй методике, изложенной ниже.

Во второй методике натяжения поводцов равномерно распределяются по длине хребтины. В этом случае начальные данные для расчета хребтины на i-м участке определяются только один раз, а именно в начале участка – точке Ai.

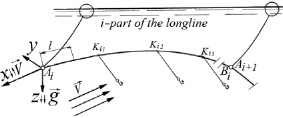
Рис. 6. I-й участок яруса при наличии течений

Математическая модель хребтины с учетом равномерно распределенных по длине хребтины сил от натяжения поводцов имеет вид

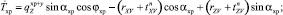
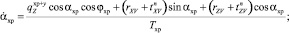
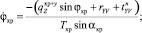(15)

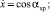
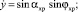
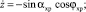
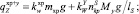
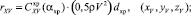
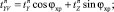
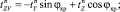
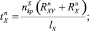
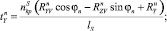
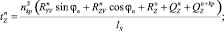
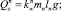
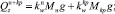
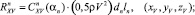
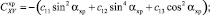
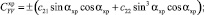
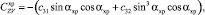(xp, n),

где 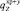– проекция на ось z веса в воде 1 м хребтины с узлами крепления к ней крючковых поводцов; Mу – масса узла крепления поводца к хребтине; dхр, dп – диаметры хребтины и поводца; lп – длина поводца; – проекции на оси земной системы координат натяжений крючковых поводцов, приходящихся на единицу длины хребтины; 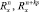, (x, y, z) – проекции гидродинамических сил поводца и наживки с крючком; αп – угол атаки поводца; Tхр, αхр, φхр – натяжение, угол атаки хребтины и угол крена плоскости потока хребтины в текущей точке; rXV, rYV, rZV – проекции гидродинамических сил, приходящихся на 1 м хребтины, на оси поточной системы координат; 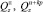– веса в воде поводца и наживки с крючком соответственно; mхр, mп – линейные плотности хребтины и поводца.

Для успешного лова гидробионтов необходимо обеспечить нахождение всех крючков в слое рыбы. Интегрируя дифференциальные уравнения

,

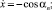
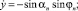
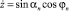получим координаты крючков в системе Aixyz (рис. 7):

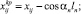
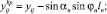
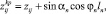
где xij, yij, zij – координаты точки крепления j-го поводца к хребтине на i-м участке яруса; 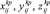– координаты крючков; ln – длина крючкового поводца (рис. 7).

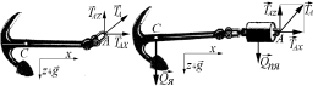
Математическая модель якоря

Якоря служат для обеспечения неподвижности яруса, заданной стрелки прогиба хребтины и увеличения скорости погружения ярусного порядка.

На промысле используются якоря без подъякорников и с подъякорниками в форме грузов, рис. 8. В общем случае натяжение якорного линя 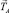в точке А его крепления к якорю имеет горизонтальную 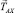и вертикальную 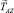составляющие. Первая из них уравновешивается держащей силой якоря 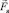, вторая – весом в воде якоря и/или подъякорника.

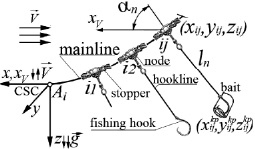
Рис. 7. К определению координат j-го рыболовного крючка на i-м участке яруса

а б

Рис. 8. Якоря: а – без подъякорника; б – с подъякорником в форме цилиндра

Максимальная горизонтальная сила которую способен удерживать якорь (держащая сила якоря), определяется по формуле

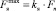
где kя – коэффициент держащей силы якоря (зависит от типа якоря и грунта); Fn – сила давления якоря на грунт, определяемая по формулам

– для якоря без подъякорника;

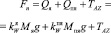– для якоря с подъякорником.

Здесь Mя, Mпя – массы якоря и подъякорника.

Масса якоря определяется по формулам:

якорь без подъякорника (рис. 8, а):

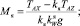(16)

якорь с подъякорником (рис. 8, б):

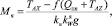(17)

где f – коэффициент трения подъякорника о грунт; Qпя – вес подъякорника в воде; TAX, TAZ – проекции на оси x и z натяжения якорного линя в точке его крепления к якорю (причем TAZ ≤ 0, так как ось z направлена по отвесу вниз, т.е. 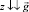); 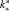, 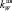– коэффициенты веса якоря и подъякорника в воде (kW = 0,87 – сталь, kW = 0,67 – бетон).

Сила TAX должна обеспечивать заданную стрелку прогиба хребтины яруса. Она определяется по формулам:

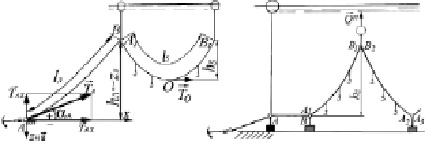
● для пелагического яруса (рис. 9, а):

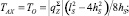(18)

● для придонного яруса (рис. 9, б):

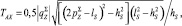(19)

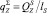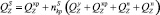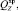
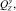
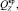
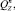
где – вес в воде яруса, приходящийся на единицу его длины; – вес в воде одной секции яруса с наживкой; 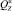– вес в воде хребтины, узла крепления поводца к хребтине, крючка, поводца, наживки; 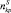– количество рыболовных крючков в секции яруса; lS – длина одной секции яруса; 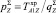– параметр яруса; hS – стрелка прогиба хребтины; TO – натяжения симметричной хребтины в нижней точке О (рис. 9, а).

Вертикальная проекция TAZ натяжения линя в точке А определяется по формуле (рис. 9, а):

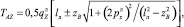(20)

где lл – длина линя; zB – аппликата точки В – конца якорного линя (zB < 0); 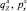– вес в воде 1 м линя и параметр линя, определяемые по формулам

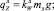
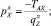
Здесь mл – линейная плотность линя; 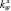– коэффициент веса в воде линя ( 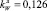– полиэстер, 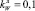– полиамид, – дэнлайн, 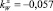– дайнекс).

а б

Рис. 9. Два типа крючковых ярусов: а – пелагический; б – придонный

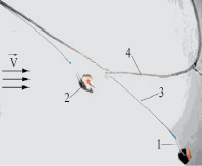
Рис. 10. Фото хребтины яруса в аэродинамической трубе при скорости воздуха 18 м/с: 1 – рыболовный крючок; 2 – наживка; 3 – крючковый поводец; 4 – хребтина

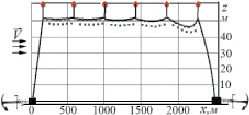
Рис. 11. Общий вид стационарного пелагического тунцеловного яруса, полученного компьютерным моделированием

В формуле (20) перед радикалом берется знак (+), если 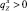, т.е. когда якорный линь тяжелее воды, и знак (–) – в противном случае.

Разработаны адекватные математические модели (2)–(20) элементов крючковых орудий рыболовства, позволяющие выполнять их математическое моделирование. Адекватность этих моделей подтверждена их испытаниями в гидродинамических лотках и аэродинамических трубах (рис. 10).

Математические модели (2)–(20) положены в основу программного комплекса «Моделирование ярусных порядков и их элементов с учётом течений CM-LongLine». Комплекс состоит из набора программ. Эти программы могут работать как автономно, моделируя отдельные элементы яруса, так и системно, моделируя весь ярусный порядок. Результаты компьютерного моделирования стационарного пелагического яруса приведены на рис. 11.

Выводы

Получен общий интеграл (4) дифференциальных уравнений (3) равновесия гибких канатов в покоящейся жидкости, являющийся обобщением работы [10] на случай, когда канат (хребтина крючкового яруса) легче воды. Он позволяет выполнять математическое моделирование любых крючковых рыболовных систем в покоящейся жидкости.

Для дрейфующих крючковых ярусов и стационарных ярусов при наличии течений разработаны математические модели их элементов: рыболовного крючка (7), крючкового поводца (8), системы «наживка – крючок – поводец» (9)–(13), узла крепления поводца к хребтине (14); гибкого каната в потоке (2); хребтины яруса (15), якоря (16)–(20). На основе этих математических моделей на языке программирования Borland Delphi разработан программный комплекс CM-LongLine (Computer Modeling LongLine), позволяющий выполнять компьютерное моделирование всех типов ярусов при наличии течений.

Рецензенты:

Азовцев А.И., д.т.н., профессор, заведующий кафедрой «Теория и устройство судов», МГУ им. адм. Г.И. Невельского, г. Владивосток;

Друзь И.Б., д.т.н., профессор, заведующий кафедрой «Теоретическая механика и сопротивление материалов», МГУ им. адм. Г.И. Невельского, г. Владивосток.

Библиографическая ссылка