Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Попов А.А. 1 Шефер О.В. 2 Рожнева О.В. 2

---

1 Марийский государственный университет

2 Томский политехнический университет

Разработана численная модель для исследования поглощения оптического излучения атмосферной средой, содержащей частицы с различными оптическими, микрофизическими и ориентационными свойствами. Поглощение определялось на основе закона сохранения энергии, учитывающего баланс между поглощением, рассеянием и ослаблением электромагнитного излучения. Для расчета оптических характеристик среды, представленной хаотически ориентированными частицами, использовалась теория Ми. Решение задачи светорассеяния для крупных кристаллов, преимущественно ориентированных в пространстве, проводилось в рамках метода физической оптики, рассматривающего векторную природу излучения. При определении поля, рассеянного в направлении вперед, учитывалась соизмеримость рефракционного и дифракционного полей. Такой подход позволил корректно и наиболее точно получить результаты расчета характеристик трансформированного излучения. Иллюстрируются особенности спектрального хода коэффициента поглощения атмосферной средой с различными микрофизическими параметрами. Показано, что несмотря на сильное поглощение ИК излучения ледяными частицами даже при качественной оценке оптических характеристик следует учитывать спектральные особенности коэффициента поглощения.

Статья в формате PDF

735 KB

численная модель

поглощение

оптическое излучение

теория Ми

метод физической оптики

атмосферные частицы

ориентация

поляризация

1. Борен К., Хафман Д. Поглощение и рассеяние света малыми частицами. – М.: Мир, 1986. – 660 с.

2. Волковицкий О.А., Павлова Л.Н., Петрушин А.Г. Оптические свойства кристаллических облаков. – Л.: Гидрометеоиздат, 1984. – 200 с.

3. Попов А.А. О когерентном сложении рассеянного и дифракционного полей в задачах светорассеяния на крупных кристаллах // Докл. АНСССР. – 1988. – Т. 303, № . 3. – С. 594–597.

4. Bi L., Yang P., Kattawar G.W., Hu Y., Baum B.A. Scattering and absorption of light by ice particles: Solution by a new physical-geometric optics hybrid method // J. Quant. Spectr. & Radiat. Transf. – 2011. – Vol. 112. – P. 1292–1508.

5. Min Q.-L., Li R., Lin B., Joseph E., Morris V., Hu Y., Li S.W., Wang S. Impacts of mineral dust on ice clouds in tropical deep convection systems // Atmospheric Research. – 2014. – Vol. 143. – P. 64–72.

6. Mishchenko M.I., Travis L.D., Lacis A.A. Scattering, Absorption, and Emission of Light by Small Particles // Cambridge. – UK: NASA, 2002.

7. Moosmüller H., Chakrabarty R.K., Arnott W.P. Aerosol light absorption and its measurement: A review // J. Quant. Spectr. & Radiat. Transf., 2009, Vol. 110, – P. 844-878.

8. Popov A.A. Characteristics of extinction for a hexagonal crystal // Proc. SPIE. – 1998. – Vol. 3220. – P. 380–389.

9. Shefer O., Popov A. Extinction and small angle scattering by thin plate crystals // Applied Optics. – 2010. – Vol. 49, № 8. – P. 1434–1445.

10. Waren S.G., Brandt R.E. Optical constants of ice from the ultraviolet to the microwave: A revised compilation // Geophys. Res. – 2008. – Vol. 113. – D14220.

11. Xie Y., Li Z., Li L., Wang L., Li D., Chen C., Li K., Xu H. Study on influence of different mixing rules on the aerosol components retrieval from ground-based remote sensing measurements // Atmospheric Research. – 2014. – Vol. 145–146. – P. 267–278.

Известно, что атмосферные образования в значительной мере воздействуют на радиационный баланс системы земля – атмосфера и определяют климат Земли [6]. Облака верхнего и нижнего ярусов могут как выхолаживать атмосферу, так и обеспечивать парниковый эффект [5, 6]. Разнообразные формы и размеры атмосферных частиц, их химический состав являются причиной многообразия оптических свойств среды. Понимание прямого и косвенного воздействия частиц на перенос излучения требует получения как фундаментальных знаний, так и достоверных экспериментальных данных оптических характеристик облаков. Необходимость проведения мониторинга и оценка физических параметров окружающей среды как в локальных, так и в глобальных масштабах привела к интенсивному развитию теоретических и экспериментальных методов исследования атмосферных образований природного и антропогенного происхождения [11]. Тем не менее исследователи указывают на существующую несогласованность экспериментальных и численных данных оптических характеристик среды [7]. Сложность численной реализации поглощения, определяемого рассеянием и ослаблением излучения атмосферными кристаллами, приводит к упрощению модели. Однако неучет ряда эффектов светорассеяния, обусловленных несферичностью и преимущественной ориентацией кристаллов, а также поляризационными особенностями трансформированного излучения, может внести существенную ошибку в расчеты оптических параметров ледяных облаков [4]. Кроме того, рассмотрение прозрачных (или полностью поглощающих лучистую энергию) кристаллов не позволяет корректно рассчитать характеристики поглощения ИК излучения полупрозрачными частицами, к которым относятся атмосферные кристаллы.

В данной работе для исследования характеристик поглощения оптического излучения предложена модель дисперсной среды, представленная сферическими частицами и кристаллами, преимущественно ориентированными в пространстве. При этом учитывается комплексный показатель преломления частиц, согласующийся с длиной волны падающего излучения.

Формализм расчета

Одной из важнейших оптических характеристик является поглощение. Определим поглощение оптического излучения после взаимодействия с частицами на основе закона сохранения энергии: «поглощение = экстинкция – рассеяние». Для отдельной частицы справедливо соотношение

S_abs = S_ext – S_sca, (1)

где S_abs – сечение поглощения; S_ext – сечение ослабления; S_sca – сечение рассеяния. Следует отметить, что рассеяние на частицах происходит во всех возможных направлениях, а ослабление определяется исходя из рассеяния в направлении строго вперед. Рассмотрим характеристики рассеяния электромагнитного излучения, необходимые для расчета составляющих поглощения (1).

Сечение рассеяния S_sca можно записать как [1]

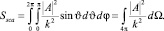(2)

Подынтегральную величину |A|²/k² называют дифференциальным сечением рассеяния, определяющим угловое распределение рассеянного света в единичном телесном угле (Ω) около рассматриваемого направления; k – волновое число (k = 2π/λ, где λ – длина волны); амплитуду рассеянного поля (А) рассматривают как скалярную характеристику, когда нет необходимости учитывать состояние поляризации излучения. При учете состояния поляризации падающего и трансформированного излучения амплитуду рассеянного поля следует определять как векторную величину. Это особенно важно, когда рассеивателями являются преимущественно ориентированные кристаллы. В этом случае А в (2) зададим как вектор A и запишем в виде суммы двух взаимно перпендикулярных векторов А₁ и А₂: А = А₁ + А₂. Комплексные амплитуды рассеянного (А₁, А₂) и падающего (Е₁, Е₂) полей связаны соотношением [1]

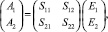(3)

где S_ij (i = 1, 2; j = 1, 2) – элементы амплитудной матрицы S. Для скалярных полей все элементы амплитудной матрицы равны между собой.

Для расчета амплитуд рассеянного поля применяются различные методы, учитывающие особенности рассеяния, обусловленные формой и размером частицы. Решение Ми [1] задачи рассеяния плоской волны на сфере является универсальной. Этот формализм может быть использован при моделировании сред, состоящих как из мелких, так и крупных частиц, причем их форма может быть не только близкой сферической, но иметь сложные объемные очертания. Выражение для расчета сечения рассеяния, полученное в приближении Ми, имеет вид

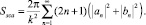(4)

Коэффициенты an и bn [1] можно определить через функции Рикки − Бесселя. Эти величины зависят от угла рассеяния, размера частиц, показателя преломления и длины волны падающего излучения.

Известно, что рассеяние системой преимущественно ориентированных кристаллов может кардинальным образом отличаться от рассеяния сферическими частицами. Чтобы учесть анизотропные свойства крупного кристалла, метод физической оптики является наиболее приемлемым для расчета характеристик светорассеяния. Следует отметить, что существует различие в формализме при определении параметров рассеяния в передней полусфере и задней полусфере.

Определим в рамках метода физической оптики векторные составляющие амплитуды поля, рассеянного в задней полусфере, обозначим их как А_B1 и А_B2 (частный случай для А₁, А₂) и определим из известных соотношений [1]

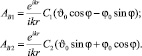(5)

Единичные орты ϑ₀, φ₀ связаны с направлением распространения волны. Углы ϑ и φ определяют в сферической системе координат направление рассеяния. Алгоритм расчета величин С₁ и С₂ продемонстрируем на примере крупного кристалла с плоскопараллельными гранями. Для определенности рассмотрим частицу пластинчатой формы. Для этого кристалла выражения С₁ и С₂ имеют вид

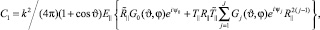
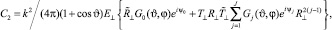(6)

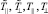где и 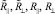‒ коэффициенты Френеля прохождения и отражения соответственно; угловые функции G₀(ϑ,φ), G_j(ϑ,φ) являются интегралами Фраунгофера, определяемые для пучков различной кратности (j) отражения; ψ₀ и ψ_j ‒ фазовые набеги отраженных и рефракционных луче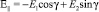й; и 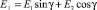(угол γ задает ориентацию плоскости поляризации).

При расчете векторной амплитуды рассеянного поля в передней полусфере следует учитывать возможную соизмеримость дифракционного и рефракционного полей. Эта особенность является принципиально значимой при расчете амплитуды трансформированного поля, прошедшего через крупный кристалл с плоскопараллельными гранями. При этом метод физической оптики позволяет когерентно сложить дифракционное поле и поле рефракционных пучков с учетом фазовых набегов [3]. Векторные составляющие амплитуды поля, рассеянного в передней полусфере, обозначим как А_S1 и А_S2

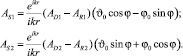(7)

Согласно принципу Бабине, амплитуды дифракционного поля A_D1 и A_D2 определяются как

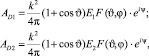(8)

где угловая функция F(ϑ, φ) является интегралом Фраунгофера; ψ ‒ фазовый набег невозмущенной части фронта волны после ее прохождения через объем, содержащий частицу. Используя методологию определения А_B1 и А_B2 (5) и (6), найдем амплитуды рассеянного поля А_R1 и А_R2 в передней полусфере. Формулы для А_R1 и А_R2 имеют вид, подобный (5) и (6). Детализированный алгоритм для расчета А_R1 и А_R2 иллюстрируется в [9].

Для определения сечения ослабления скалярных или неполяризованных полей используют известное соотношение [1]

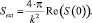(9)

В случае поляризованных полей выражение для сечения ослабления имеет вид [1]

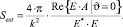(10)

Амплитудная матрица S размерностью 2×2 при угле рассеяния ϑ = 0 преобразуется в скалярную величину, то есть S_ij = S(0).

Один из основных выводов, который следует из анализа (10), состоит в том, что излучение различной поляризации ослабляется по-разному [3]. Моделирование процесса ослабления излучения различными дисперсными средами связано с выполнением трудоемких расчетов. Оно включает в себя численное представление результата решения задачи рассеяния на отдельной частице. Для большинства моделей полидисперсных сред определение характеристик ослабления связано с выполнением трудоемких расчетов. Тем не менее существуют модели, имитирующие атмосферные частицы, для которых получены соотношения для определения экстинкции в простой форме. В частности, к таким формулам относится соотношение для расчета сечения ослабления, полученное в рамках теории Ми 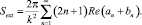[1]:

(11)

Для расчета ослабления крупными кристаллами можно указать формулы, полученные в приближении метода физической оптики с учетом когерентного сложения дифракционного и рефракционного полей [8]:

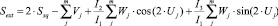. (12)

Для гексагонального столбика m = 3, для прямоугольного (а также пластинки) – m = 2. Величины V_j и W_j определяются через амплитуды рассеянного поля, U_j представляет собой комбинацию углов Эйлера, задающих положение тела в пространстве, S_sq – площадь тени частицы. Из всех крупных частиц по характеру ослабления выделяются пластинки. Для этой формы частиц фактор ослабления может принимать значение из наибольшего промежутка от 0 до 4 [9].

Моделирование процесса ослабления излучения дисперсной средой обязывает рассматривать такую интегральную характеристику как коэффициент поглощения. Наиболее простой переход от поглощения одной частицей к поглощению системой частиц может быть проведен как

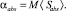(13)

Здесь 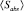– среднее сечение поглощения; М – концентрация частиц в единице объема. Учитывая функцию распределения частиц по размерам, коэффициент поглощения αabs может быть представлен в интегральной форме, подынтегральная функция которой содержит в качестве сомножителя сечение поглощения излучения частицей, имеющей размер а,

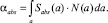(14)

Здесь величина а для сферы является радиусом, для пластинчатого кристалла – радиусом окружности, вписанной в основание пластинки; N(a) – функция распределения частиц по размерам. Для основных видов кристаллов получены соотношения между основными размерами (например, между толщиной и длиной частицы) [2]. Так, для пластинчатых кристаллов при определенных условиях роста справедливо следующее соотношение: L = 2,020×(2⋅a)^0,449. Подобная взаимосвязь существенно упрощает численные расчеты при переходе от отдельного кристалла к ансамблю частиц.

Моделирование микроструктуры среды базируется на знании функции распределения частиц по размерам. Из многочисленных натурных исследований атмосферных образований при различных температурных режимах установлено, что распределение частиц по размерам имеет ярко выраженный максимум. При этом модифицированное гамма–распределение

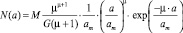(15)

адекватно описывает спектр размеров ансамбля частиц кристаллического облака [2]. Формула (15) включает в себя следующие параметры: М – концентрация пластинок, величина a_m определяет размер кристалла, соответствующий максимуму функции N(a), μ − безразмерный параметр, характеризующий крутизну склонов данного максимума, G(μ + 1) – гамма функция. Для анализа экспериментальных данных следует использовать средний радиус частиц, с учетом (15) определяется как .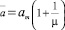

Обсуждение результатов расчета

Нами выполнено численное исследование спектральной зависимости коэффициента поглощения для сферических частиц и для пластинчатых кристаллов.

Численная модель, используемая в данной работе для расчета ослабления, кроме условия a ≈ λ включает в себя и предельные случаи, когда a << λ и a >> λ. Так, для мелких частиц, когда их размеры много меньше длины волны падающего излучения λ, такое рассеяние, как правило, называют рэлеевским. Если преобладающую роль в экстинкции играет поглощение, то спектр экстинкции изменяется как 1/λ. Если же доминирует рассеяние, то спектр экстинкции ведет себя как 1/λ⁴ и с уменьшением длины волны ослабление увеличивается. В случае, когда размеры частиц много больше длины волны, значение сечения ослабления определяется как S_ext = 2S_sq (S_sq – площадь тени частицы). При этом из потока изымается в два раза больше излучения, чем падает на частицу. Ослабление крупной полупрозрачной частицей сферической формы не зависит от оптических свойств рассеивателя.

Для расчета коэффициента поглощения входными параметрами являлись: длина волны (λ), состояние поляризации падающего излучения, геометрические размеры частиц (a), значения комплексного показателя преломления (n, χ), параметры распределения частиц по размерам (M, μ, a_m). Для определенности рассматривалось линейно поляризованное падающее излучение и нормальное расположение пластинок относительно направления распространения фронта волны. При расчете спектральной зависимости α_abs(λ) использовались данные n = n(λ) и χ = χ(λ) для льда [10].

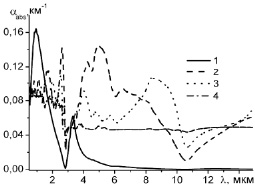
Рис. 1. Спектральные зависимости коэффициента поглощения (αabs(λ)) для 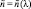[10] при μ = 10, М = 1 л^–1:

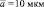1 – ; 2 – ; 3 – ; 4 –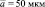

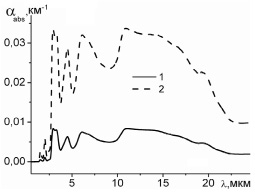
Рис. 2. Спектральные зависимости αabs(λ) при 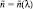[10], μ = 10, M = 1 л^–1: 1 – 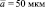; 2 –

На рис. 1 представлены результаты расчета коэффициента поглощения системой сферических частиц с различными средними размерами. Из рис. 1 видно, что наиболее яркие изменения поглощения αabs(λ) наблюдаются в случае, когда размеры частиц сравнимы с величиной длины волны. Особенности спектрального хода α_abs(λ) связаны со средними значениями радиусов сфер и значениями показателя преломления. Для частиц, средние размеры которых более чем на порядок отличаются от величины длины волны, в области среднего ИК диапазона наблюдается практически нейтральный ход α_abs(λ).

На рис. 2 иллюстрируются спектральные зависимости коэффициента поглощения при различных средних размерах пластинок. Спектральный ход кривой α_abs(λ) зависит в основном от характера изменения показателя поглощения χ. Большему радиусу пластинки соответствует большая толщина и более сильное поглощение. Однако даже для крупных пластинок не происходит полного поглощения оптического излучения, прошедшего внутрь пластинки.

Заключение

В работе представлен алгоритм расчета коэффициента поглощения оптического излучения, в основе которого положен закон сохранения энергии. При этом рассматривались характеристики ослабления, рассеяния и поглощения, полученные в рамках теории Ми, для мелких частиц, соизмеримых с длиной волны и многократно превышающих ее по величине. В приближении метода физической оптики для крупных преимущественно ориентированных в пространстве кристаллов получены соотношения для определения коэффициента поглощения.

Иллюстрируется зависимость спектрального хода коэффициента поглощения от микрофизических параметров частиц. Показано, что хотя для крупных атмосферных кристаллов свойственно сильное поглощение ИК излучения, тем не менее даже при качественной оценке экспериментальных данных оптических характеристик ледяных облаков следует учитывать эти частицы.

Работа выполнена по заданию № 645 (код проекта 4.1349.2014) Минобрнауки РФ.

Рецензенты:

Журавлева Т.Б., д.ф.-м.н., ведущий научный сотрудник Института оптики атмосферы им. Зуева Сибирского отделения Российской академии наук (ИОА СО РАН), г. Томск;

Войцеховская О.К., д.ф.-м.н., профессор кафедры квантовой электроники и фотоники, Радиофизический факультет, Национальный исследовательский Томский государственный университет, г. Томск.

Работа поступила в редакцию 17.04.2015.

Библиографическая ссылка