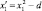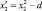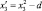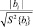Современные технологии и методы позволяют управлять структурой и свойствами материалов на цементном вяжущем. Одним из эффективных среди них является использование волновых методов активации воды затворения, к которым относится воздействие низкочастотным ультразвуковым полем. В процессе изучения данного вопроса появилась идея, что вода в любом её состоянии является маточным раствором, если в воде есть реагенты, способные откликнуться на ультразвуковое воздействие. В частности, низкопроцентное содержание гидравлического вяжущего в маточном растворе после воздействия ультразвуковым полем может обеспечивать получение материалов с повышенными технико-эксплуатационными характеристиками.
В исследовании под маточным раствором понимается раствор, в котором частицы являются центрами кристаллизации, сопровождающейся диспергированием, располагаются на определенных энергетических уровнях в соответствии с их массами и размерами [5].
По существующему определению маточный раствор – остаточная жидкость после процессов кристаллизации. Маточный раствор может содержать непрореагировавшие материалы, промежуточные продукты или примеси в существенном количестве, а также использоваться для дальнейшей обработки [4].
Для волновой активации маточного раствора нужно найти оптимальные параметры воздействия ультразвука на воду, т.е. нужно определить мощность ультразвуковых колебаний, время воздействия ультразвука и количество вводимого цемента в воду. Для этого в данной работе использовалась методика полного факторного эксперимента.
Для того чтобы применить методику полного факторного эксперимента, необходимо определить варьируемые факторы и интервалы варьирования. В качестве факторов были выбраны время воздействия ультразвука на воду, количество вводимого цемента в воду и мощность ультразвуковых колебаний (табл. 1). Результирующей функцией (Y1) выбрана прочность материала при испытании на сжатие. Согласно предварительным исследованиям функции отклика должны быть нелинейными, поэтому факторы будут иметь три уровня варьирования.
В ходе проведения исследования необходимо выяснить, как влияют выбранные факторы на основное физико-механическое свойство материала, а именно на предел прочности при сжатии.
Для того чтобы найти коэффициенты полинома, в исследовании использовался ортогональный центрально-композиционный план второго порядка (табл. 2).
Использование ортогонального планирования позволило получить независимые оценки коэффициентов регрессии с минимальной дисперсией. Ортогональность центрально-композиционного плана обеспечивается соответствующим подбором звездного плеча α (для трех факторов α = 1,2154 [2]) и специальным преобразованием квадратичных переменных 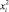 по формуле
по формуле
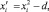
где d – поправка, зависящая от числа факторов, для трех факторов d = 0,7303 [1].
Значимость коэффициентов регрессии проверялась по критерию Стьюдента. В нашем случае для 3-х степеней свободы и 95 %-ном уровне значимости t = 2,776445105 [3].
Количество регулируемых факторов в исследовании равно 3, тогда уравнение модели примет следующий вид:
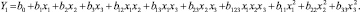
Таблица 1
Факторы и уровни их варьирования
|
Факторы |
Нижний уровень (–1) |
Основной уровень (0) |
Верхний уровень (+ 1) |
|
Обозначение |
х1 |
х2 |
х3 |
|
Время воздействия ультразвука на воду |
60 с |
180 с |
300 с |
|
Количество вводимого цемента в воду |
11 г |
12 г |
13 г |
|
Мощность ультразвуковых колебаний |
120 В∙А |
130 В∙А |
140 В∙А |
Таблица 2
Матрица ортогонального центрально-композиционного плана второго порядка и результаты экспериментов
|
Номер опыта |
x1 |
x2 |
x3 |
|
|
|
Y1 |
|
1 |
+1 |
+1 |
+1 |
0,2697 |
0,2697 |
0,2697 |
62,76 |
|
2 |
–1 |
+1 |
+1 |
0,2697 |
0,2697 |
0,2697 |
30,59 |
|
3 |
+1 |
–1 |
+1 |
0,2697 |
0,2697 |
0,2697 |
35,31 |
|
4 |
–1 |
–1 |
+1 |
0,2697 |
0,2697 |
0,2697 |
31,08 |
|
5 |
+1 |
+1 |
–1 |
0,2697 |
0,2697 |
0,2697 |
38,43 |
|
6 |
–1 |
+1 |
–1 |
0,2697 |
0,2697 |
0,2697 |
34,51 |
|
7 |
+1 |
–1 |
–1 |
0,2697 |
0,2697 |
0,2697 |
34,81 |
|
8 |
–1 |
–1 |
–1 |
0,2697 |
0,2697 |
0,2697 |
32,65 |
|
9 |
1,2154 |
0 |
0 |
0,7469 |
–0,7303 |
–0,7303 |
49,04 |
|
10 |
–1,2154 |
0 |
0 |
0,7469 |
–0,7303 |
–0,7303 |
36,62 |
|
11 |
0 |
1,2154 |
0 |
–0,7303 |
0,7469 |
–0,7303 |
31,77 |
|
12 |
0 |
–1,2154 |
0 |
–0,7303 |
0,7469 |
–0,7303 |
39,12 |
|
13 |
0 |
0 |
1,2154 |
–0,7303 |
–0,7303 |
0,7469 |
32,22 |
|
14 |
0 |
0 |
–1,2154 |
–0,7303 |
–0,7303 |
0,7469 |
39,85 |
|
15 |
0 |
0 |
0 |
–0,7303 |
–0,7303 |
–0,7303 |
30,45 |
Таблица 3
Проверка значимости коэффициентов регрессии по факторной обработке прочности материала при испытании на сжатие (Y1)
|
Коэффициенты регрессии |
Проверка коэффициентов регрессии по критерию Стьюдента |
||
|
Численное значение |
S2{bi} |
|
|
|
b0 |
33,825 |
0,849202 |
17,55 |
|
b1 |
8,191 |
1,162824 |
7,6 |
|
b2 |
3,255 |
1,162824 |
3,02 |
|
b3 |
3,854 |
1,162824 |
3,57 |
|
b12 |
3,713 |
1,592254 |
2,94 |
|
b13 |
1,29 |
1,592254 |
1,02 |
|
b23 |
2,685 |
1,592254 |
2,13 |
|
b123 |
3,283 |
1,592254 |
2,59 |
|
b11 |
4,897 |
2,918685 |
2,87 |
|
b22 |
–0,103 |
2,918685 |
–0,06 |
|
b33 |
0,297 |
2,918685 |
0,17 |
Из табл. 3 видно, что значимыми коэффициентами являются b0, b1, b2, b3, b12, b11.
Расчет коэффициентов регрессии по факторной обработке прочности материала при испытании на сжатие осуществлялся на персональном компьютере. Уравнение регрессии будет выглядеть следующим образом:
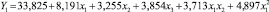
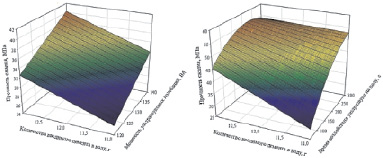
а б
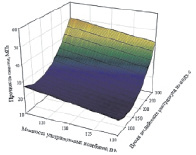
в
Рис. 1. Поверхность отклика прочности на сжатие: а – в зависимости от количества вводимого цемента и мощности ультразвуковых колебаний; б – в зависимости от времени воздействия ультразвука на воду и количества вводимого цемента; в – в зависимости от времени воздействия ультразвука на воду и мощности ультразвуковых колебаний
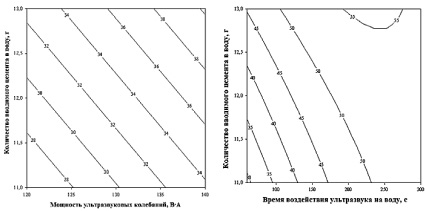
а б
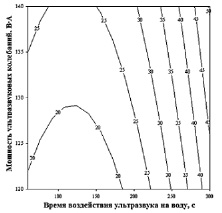
в
Рис. 2. Сечение поверхности отклика прочности на сжатие: а – в зависимости от количества вводимого цемента и мощности ультразвуковых колебаний; б – в зависимости от времени воздействия ультразвука на воду и количества вводимого цемента; в – в зависимости от времени воздействия ультразвука на воду и мощности ультразвуковых колебаний
Проверку на адекватность полученных уравнений проводили по критерию Фишера.
В нашем случае при f1 = 15 – 3 – 1 = 11; f2 = 3 – 1 = 1 и 95 %-ном уровне значимости F = 19,4. Дисперсия адекватности определялась по методике, предложенной в работах [2, 3].
Расчетные значения критерия Фишера составили F = 2,044. Следовательно, полученное уравнение регрессии адекватно описывает исследуемый процесс. Для построения поверхностей откликов использовалась программа SigmaPlotv.11.0.
Графические зависимости при варьировании выбранных параметров после статистической обработки экспериментальных данных приведены на рис. 1, 2.
В результате проведения полного факторного эксперимента были получены оптимальные параметры волновой активации маточного раствора. Оптимальными параметрами являются: время воздействия ультразвука на воду – 300 секунд, количество вводимого цемента – 13 грамм, мощность ультразвуковых колебаний – 140 В∙А.
Рецензенты:
Грейсух Г.И., д.т.н., профессор, зав. кафедрой «Физика и химия», Пензенский государственный университет архитектуры и строительства, г. Пенза;
Степанов С.А., д.ф.-м.н., профессор, Пензенский государственный университет архитектуры и строительства, г. Пенза.
Работа поступила в редакцию 17.04.2015.
Библиографическая ссылка
Фокин Г.А., Гуськов А.С. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ВОЛНОВОЙ АКТИВАЦИИ МАТОЧНОГО РАСТВОРА // Фундаментальные исследования. 2015. № 2-17. С. 3733-3737;URL: https://fundamental-research.ru/ru/article/view?id=37847 (дата обращения: 28.02.2026).