Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Погорелова А.С. 1

---

1 Муромский институт (филиал) ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»

В работе рассматриваются процессы сепарирования, фильтрования и сортирования трудно разделяемых смесей. При разделении семян с помощью силы потока воздуха растет эффект сепарирования. С учетом режима работы агрегатов и их характеристик, физико-механических свойств и состава многокомпонентных смесей разработана математическая модель сепарирования сыпучих смесей с учетом силы воздушного потока и на основе рассеивания траектории полета частиц в бункере агрегата с целью повышения технико-экономических показателей сепарирующих машин. Для трудно разделяемых сыпучих смесей при сортировании и разделении по линейному размеру, массам и составу надо использовать специальные агрегаты, где можно уменьшить значения коэффициента сцепления частиц друг с другом. В связи с этим в работе рассмотрены условия наиболее полного (глубокого) отделения получаемого продукта от примесей и отходов в широком диапазоне их засоренности. Для сепарирования продуктов в зависимости от шероховатости, формы и комплекса физико-механических свойств используются различные сепараторы. При разработке и усовершенствовании математической модели коэффициент сцепляемости частиц вводится как основной параметр, используя который можно подобрать режим работы сепаратора и технические характеристики сита.

Статья в формате PDF

828 KB

смесь

математическая модель

сепарирование

частица

воздушный поток

1. Атауллаев А.Х., Ключкин В.В. Анализ движения слоя частиц ситовой поверхности в случае поддува. – М., 1991. – 7 с. – Деп. в ВИНИТИ 1991, N 1169.

2. Атауллаев А.Х., Равшанов Н. К вопросу сепарирования сыпучих смесей в вертикальном воздушном потоке – М., 1991. – 5 с. – Деп. в ВИНИТИ 1991, N1169.

3. Атауллаев А.Х., Толчинский Ю.А., Ключкин В.В. О броуновской и фильтрационной аналогиях в процессе сепарирования с поддувом и без него. – М., 1984. – 12 с. – Деп. в ВИНИТИ 1984, № 1093.

4. Гортинский В.В., Демский А.Б, Боринский М.А. Процессы сепарирования на зерноперерабатывающих предприятиях. – М.: Колос, 1973. – С. 121–127.

5. Непомнящий Е.А. Расчет эффективности ремонтного сепарирования переменной толщины зернового слоя // Известия ВУЗов СССР. Пищевая технология. – М., 1968. – № 3. – С. 127–131.

6. Непомнящий Е.А. Переменные теории случайных процессов к определению закономерности сепарирования смесей // Труды ВНИИЗ. – М., 1989. – Вып. 42. – С. 47–56.

7. Самарский А.А., Михайлов А.П. Математическое моделирование и вычислительный эксперимент. – М.: Наука, 2001.

8. Цециновский В.М. Методы оценки технологического эффекта сепарирования // Труды ВНИИЗ. – Вып. 44. – 1963.

Исследования связаны с определением наиболее выгодных условий, при которых обеспечивается максимальная производительность агрегатов, уменьшение потерь сырья, снижение затрат ресурсов, износа оборудования и т.д. Для достижения этих целей при сепарировании сыпучих смесей на поверхности сепарирующих агрегатов создаются условия, при которых каждая частица могла бы быстро пройти через слой смеси и максимально контактировать с поверхностью сита, а вероятность столкновения частиц друг с другом была бы минимальной.

Один из путей глубокого исследования этих процессов – математическая модель (ММ). Надо подчеркнуть, что за счет силы поддува воздушного потока разрыхляется слой сыпучей смеси, в результате чего время просеивания ядер по толщине основной массы линейно уменьшается. Это приводит к росту прохода частиц через отверстия сита и повышению производительности сепарирующих агрегатов.

Цель работы – рассмотреть процессы сепарирования, разработать математическую модель сепарирования и фильтрования трудно разделяемых смесей.

Математическая модель сепарирования и фильтрования трудно разделяемых смесей

Разделение сыпучих смесей с большими значениями коэффициентов сцепления и трудно разделяемыми свойствами c целью предварительной очистки необходимо исследовать в зависимости от линейных размеров и массы, сцепляемости частиц друг с другом, засоренности смеси и других факторов. Их предварительное разделение осуществляется с помощью сепарирующего агрегата, режим работы которого основан на рассеивании траектории полета частиц, уносимых воздушным потоком [1].

Для вывода математического моделирования (ММ) таких процессов предположим, что на слой сыпучей смеси действуют следующие силы: P_g – сила давления потока на частицу, направленная так же, как и вектор скорости потока; R_c – сила сопротивления слоя сыпучей смеси, направленная обратно по отношению к скорости движения частиц; N_c – сила нормальной реакции сита. Угол, образованный вектором скорости полета с осью z, обозначим через α₁, угол между вектором скорости частицы и поверхностью сита – α₂ (рисунок). ММ разработано при движении частицы, уносимой воздушным потоком к всасывающему отверстию от поверхности сита, вибрирующего по гармоническому закону, и на слой сыпучей смеси действуют следующие силы: Р_c – сила давления потока воздуха, действующая на частицу, направленная по скорости потока; R_c – сила сопротивления слоя сыпучей смеси, направленная противоположно скорости движения частиц; R_а – сила сопротивления воздуха, направленная обратно скорости движения частиц.

В такой постановке задачи имеем следующее ММ:

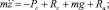
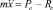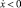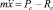при ,

при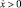

или

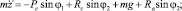
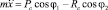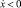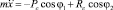при ,

при .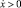

Угол, образованный вектором скорости потока с осью x, обозначим через φ₁, угол между вектором скорости частиц и осью x – через φ₂.

Начало координат выберем в центре отверстия трубы сепаратора. Тогда уравнение движения частицы принимает вид

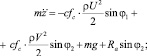
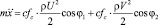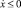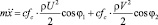при ,

при ,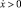

где f_c – коэффициент сопротивления слоя сыпучей смеси; ρ – плотность воздуха; с – коэффициент сопротивления воздуха.

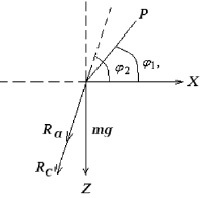
Схема сил, действующих на частицы сыпучих смесей

Так как скорость перемещения частиц является первой производной по времени от координаты, т.е.

V_z = z, V_x = x,

следовательно,

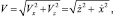
а скорость потока определяется следующим образом:

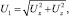
где

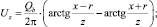
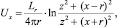
Q_b – расход воздуха в трубе сепаратора; L_T – длина трубы; r – радиус трубы.

С учетом того, что

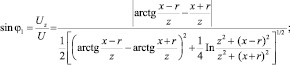
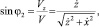
ММ нестационарного технологического процесса сепарирования и фильтрования смесей окончательно принимает вид

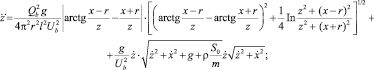
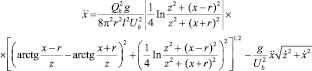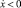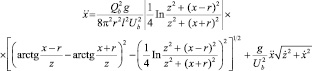при ,

при ,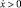

где U_b – скорость витания сыпучей смеси; l – диаметр трубы сепаратора; S₀ – площадь отверстия трубы.

Система уравнений нелинейная и выписать ее решение в аналитическом виде невозможно. Эту систему с начальными условиями можно решить численно, например методом Рунге – Кутты. Вычислительные эксперименты (ВЭ) были проведены для различных значений r, l, Q, U_b. Из анализа вычислительного эксперимента следует, что скорость полета частиц со временем по вертикали линейно уменьшается [7]. С уменьшением скорости полета по вертикали линейно растет скорость перемещения частиц относительно оси ох. Со временем перемещения скорости частиц по вертикали и горизонтали уменьшаются. С подъемом частиц по вертикали скорость перемещения их по горизонтали часто меняет свой знак. За счет этого частицы сыпучей смеси начинают перемещаться хаотично [2].

Беспорядочное движение частиц растет с резким ростом расхода воздуха в трубе, в результате чего разделение сыпучей смеси, в зависимости от линейных размеров частиц, затрудняется [3]. Частицы сыпучей смеси принимают состояние равновесия при 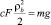, а когда 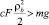, они поднимаются вверх и движутся по направлению воздушного потока.

Так же можно рассмотреть сепарирование трудно разделяемых смесей на основе рассеивания траектории полета частиц. Особенности сепарирования и сортирования трудно разделяемых смесей, заключаются в том, что у них коэффициент сцепления частиц друг с другом имеет большое значение [8]. Для их сортирования и разделения по линейному размеру, массам и составу надо использовать специальные агрегаты, где можно уменьшить значения коэффициента сцепления частиц друг с другом. В связи с этим нужно выявить условия наиболее полного (глубокого) отделения получаемого продукта от примесей и отходов в широком диапазоне их засоренности. Отметим, что сепарирование сыпучей смеси через ситовую поверхность без учета ее предварительной очистки от крупных примесей методом поддува невыгодно тем, что отверстия сепаратора часто забиваются и уменьшается эффективность его работы.

Для совокупности частиц, в которой критические скорости изменяются от 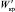до 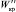, рассеивание траекторий полета частиц в зависимости от размера масс, упругости и физико-механических свойств под действием вертикального поддува воздушным потоком характеризуется разностью (β″ − β′):

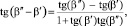
где β′, β″ – направление относительной скорости частиц.

Траектория движения частиц в канале под действием потока воздуха определяется из решения системы уравнений:

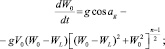
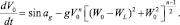
Здесь W_o, V_o – компоненты относительной скорости перемещения частиц; α_g – угол между вектором скорости воздуха и вертикалью; W_L – скорость воздуха в канале сепаратора. Сепарирование с помощью воздушного потока обеспечивает разделение и отбор биологически наиболее полноценных семян [4]. Доведение до высоких степеней разделения от биологически неполноценных и от инородных примесей связано с определением жестких границ скоростей потока воздуха и углов ее подачи в зависимости от размера и массы. В пневмосепарирующий канал поступает поток семян или другой сыпучей смеси и встречается с потоком воздуха. При встрече поток сыпучей смеси изменяет свое направление и скорость. Начальная скорость движения частиц определяется следующим образом:

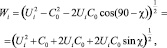
где С_o – начальная скорость подачи сыпучей смеси в канале сепарирующего агрегата; χ – угол подачи сыпучей смеси (относительно горизонта); U_н – начальная скорость воздушного потока.

При разделении семян с помощью силы потока воздуха растет эффект сепарирования [5]. К числу факторов, влияющих на эффект очистки, относится степень различия скоростей витания очищенной сыпучей смеси от примесей. Чем меньше отличие скоростей витания, тем ниже эффект очистки. Также на него влияет средняя скорость воздушного потока. При достижении этой скоростью некоторого предельного значения происходит унос нормальных зерен в отходы. В связи с этим особое внимание уделяется определению оптимальной величины средней скорости воздушного потока. В основном влияние на эффект очистки оказывает равномерность потока в канале. Отметим, что при сепарировании сыпучей смеси с помощью метода поддува и отcоса образовавшаяся при обрушивании сепарируемых материалов уносится потоком воздуха или частью отхода [6]. Это приводит к потере большой части ценного продукта, так как под действием силы поддува не успевают пыльные частицы просеивать до нижнего слоя сепарируемого материала.

ММ перемещения сыпучей смеси под действием совокупности сил описывается с помощью уравнений

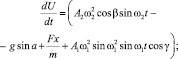
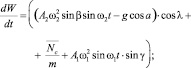
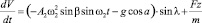
с начальными условиями

U(0) = 0, W(0) = 0, V(0) = 0,

где

Из постановки задачи видно, что при совпадении направления силы пульсации с силой нормальной реакции сита сила тяжести масса каждой частицы уменьшается на G = mg – F_n, где 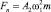. Таким образом, сила пульсации во всех случаях влияет на движение частиц сыпучей смеси. В таком случае полная реакция сита складывается из силы нормальной реакции сита N_c и силы вертикальной пульсации сита F_n.

Оценка членов уравнения движения частиц показала, что за счет силы пульсации сита снижается давление сепарируемого слоя, в результате чего разрыхляется слой сыпучей смеси. Это приводит к росту коэффициента сепарирования, а вслед за ним растет вероятность прохода частиц по толщине слоя сепарирования. В результате этого сила инерции складывается с силой нормальной реакции и пульсации сита. Это приводит к улучшению условия прохода сыпучей смеси через отверстия сита и толщину слоя сепарирования.

Заключение

Таким образом, сепарирование и фильтрование смесей исследовано как комплекс взаимосвязанных систем, который позволяет рассмотреть объект с учетом параметров работы сита, скоростей перемещения частиц, физико-механических свойств и состава сыпучей смеси, режимов работы агрегатов. Предложенный подход позволяет повысить степень адекватности разрабатываемых математических моделей. Проведенными численными расчетами установлено, что весь ход технологического процесса зависит от коэффициента сцепления частиц и толщины слоя сепарирования. Обоснована необходимость проведения исследования на основе разработанных ММ: сепарирование, сортирование, разделение и фильтрование сыпучих смесей, в результате чего можно определить диапазоны изменения параметров работы сепарируемых агрегатов и машин, а также фильтровальных колонок.

Рецензенты:

Булкин В.В., д.т.н., профессор кафедры «Техносферная безопасность», Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, филиал, г. Муром;

Орлов А.А., д.т.н., доцент, заведующий кафедрой «Физика и прикладная математика», Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, филиал, г. Муром.

Работа поступила в редакцию 17.04.2015.

Библиографическая ссылка