Актуальность исследований процессов образования и разложения газогидратов в пористых средах обусловлена все возрастающим интересом к проблеме газогидратов, связанным, в первую очередь, с признанием того факта, что в перспективе природные газогидраты могут стать новым источником углеводородного газа благодаря значительным ресурсам, неглубокому залеганию и концентрированному состоянию в них газа [1, 3]. В связи с этим за последние годы резко возрос интерес к исследованиям и разработкам технологий, позволяющих использовать газогидраты в виде альтернативного углеводородного сырья.
Общепринятые способы извлечения природного газа из газовых гидратов включают воздействие нагревания и/или пониженного давления на газовые гидраты с целью высвобождения природного газа. Однако данные способы требуют подвода к системе значительного количества энергии, что ведет к высоким затратам на извлечение. Одним из вариантов решения данной проблемы могла бы быть разработка таких технологий добычи газа из газогидратов, при которых разложение гидрата происходит не на газ и воду, а на газ и лед. Это позволило бы уменьшить энергетические затраты на разработку газогидратных месторождений, поскольку удельная теплота фазового перехода гидрат-лед значительно ниже теплоты перехода гидрат-вода. Очевидно, что данные технологии должны быть подкреплены соответствующими расчетами по теоретическим моделям, адекватно отражающим реальные условия.
Математическая модель процесса разложения газогидрата в пористой среде на газ и воду для случая протекания фазовых переходов на фронтальной границе построена в работах [2, 6, 7]. Некоторые особенности процесса образования газогидрата в пористой среде рассмотрены в работах [4,5]. В настоящей работе представлено решение задачи о диссоциации газогидрата в пористой среде при депрессионном воздействии в случае формирования объемной области фазовых переходов.
Постановка задачи и основные уравнения
Для описания процессов тепломассопереноса, сопровождающихся диссоциацией газогидрата в пористой среде, примем следующие допущения. Процесс однотемпературный, т.е. температуры пористой среды и насыщающего вещества (газа, гидрата или воды) совпадают. Гидрат является двухкомпонентной системой с массовой концентрацией газа G. Кроме того, скелет пористой среды, газогидрат и вода несжимаемы и неподвижны, пористость постоянна, газ является калорически совершенным.
В рамках отмеченных допущений запишем для осесимметричной задачи уравнения сохранения массы, закон Дарси, уравнения состояния газа и притока тепла (без учета баротермического эффекта):
,
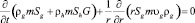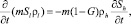
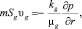(1)
.
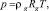
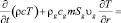
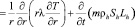Здесь m – пористость; p – давление, T – температура; ρj и Sj – истинная плотность и насыщенность пор j-й фазы (j = h, l, g); индексы h, l и g относятся к параметрам гидрата, воды и газа соответственно; υg, kg и μg – скорость, проницаемость и динамическая вязкость для газовой фазы; Lh – удельная теплота разложения гидрата; cg – удельная теплоемкость газа; ρc и λ – удельная объемная теплоемкость и коэффициент теплопроводности системы.
Зависимость коэффициента проницаемости для газа kg от газонасыщенности можно задать на основе формулы Козени
.
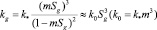Значения температуры и давления в области разложения гидрата связаны условием фазового равновесия [1]
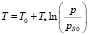, (2)
где T0 – исходная температура системы, ps0 – равновесное давление, соответствующее исходной температуре, T* – эмпирический параметр, зависящий от вида газогидрата.
При диссоциации газогидрата в пористом пласте возникают зоны, в которых газ, вода и гидрат могут находиться в различных состояниях. На поверхностях разрыва между этими зонами, где терпят скачки насыщенности фаз, а также потоки массы и тепла, выполняются соотношения, следующие из условий баланса массы и тепла:
,
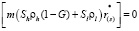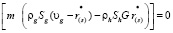, (3)
.
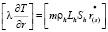Здесь [ψ] – скачок параметра ψ на границе между зонами;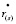 
– скорость движения этой границы; нижний индекс в скобках (s) относится к параметрам на границе между зонами. Температура и давление на этих границах полагаются непрерывными.
Будем полагать, что пласт в начальный момент времени насыщен газом и газогидратом, давление p0 и температура T0 которых в исходном состоянии соответствуют термодинамическим условиям существования их в свободном состоянии (p0 > ps0). Пусть давление и температура изначально одинаковы во всем пласте
t = 0: T = T0, p = p0 (r > rw).
Пусть через скважину, вскрывшую пласт на всю толщину, отбирается газ с постоянным массовым расходом Q (на единицу высоты скважины) при условии отсутствия кондуктивного потока тепла на границе скважины. В результате отбора газа в пласте возникает три характерные области: ближняя (первая), где поры заполнены газом и льдом (водой), промежуточная (вторая), в которой газ, лед (вода) и гидрат находятся в равновесии, и дальняя (третья), которая заполнена газом и гидратом. Во второй зоне происходит диссоциация гидрата. Соответственно возникают две подвижные поверхности: между дальней и промежуточной областями, где начинается плавление гидрата, и между ближней и промежуточной областями, на которой заканчивается процесс разложения гидрата. Исходная гидратонасыщенность пласта ν равна гидратонасыщенности третьей области и постоянна во всех точках этой области.
Рассматривая достаточно большие времена после начала отбора газа, когда радиус ближней (первой) области значительно превышает радиус скважины rw, можно полагать, что размер скважины слабо сказывается на особенностях протекания процесса. Тогда с учетом закона Дарси и уравнения состояния для газа условия на границе скважины имеют вид:
,
.
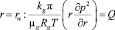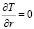
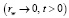Автомодельное решение
Сформулированная задача имеет автомодельное решение. Введем автомодельную переменную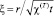 
, где χ(T) = λ/ρc – коэффициент температуропроводности пласта.
В автомодельных переменных решение для распределения давления (после применения метода линеаризации Лейбензона) и температуры в каждой из областей может быть записано в виде:
a) в ближней области (0 < ξ < ξ(s)):
,
, 
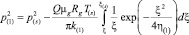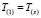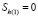; (4)
б) в промежуточной области (ξ(s) < ξ < ξ(m)):
,
, 
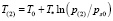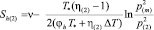; (5)
в) в дальней области (ξ(m) < ξ <∞(m)):
,
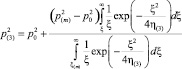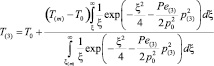, (6)
.
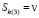Здесь
, 
, 
, 
, 
,
, 
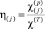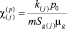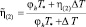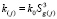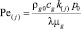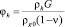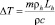, ρg0 – плотность газа при давлении p0.
Параметры первой, второй и третьей областей снабжены нижними индексами в скобках j = 1, 2 и 3; нижний индекс в скобках (s) и относится к параметрам на границе между первой и второй областями, (m) – между второй и третьей зонами соответственно.
На основе решений (4) – (6) и условий баланса массы и тепла (3) на межфазных границах получена система трансцендентных уравнений, исходя из которой численно определяются автомодельные координаты данных границы и значения параметров на них.
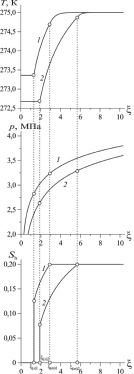
Рис. 1. Распределение по переменной ξ температуры, давления и гидратонасыщенности: Q = 0,035 кг/(м·с) (1), Q = 0,045 кг/(м·с) (2)
Результаты расчетов
На рис. 1 приведены распределения давления, температуры и гидратонасыщенности для разных значений массового расхода отбора метана из гидратосодержащего пласта. Для параметров, характеризующих систему, приняты следующие значения: m = 0,1, G = 0,12, ν = 0,2, p0 = 5 МПа, T0 = 275 К, T* = 10 К, ps0 = 3,3 МПа, Rg = 520 Дж/(К∙кг), k0 = 10-14 м2, ρh = ρi = = 900 кг/м3, ρc = 2,5∙106 Дж/(К·кг), cg = 1560 Дж/(К·кг), λ = 2 Вт/(м∙К), μg = 10-5 кг/(м∙с), Lh = 5·105 Дж/кг. В соответствии с рисунком, если массовый расход отбора газа достаточно велик (кривая 2), то температура на границе, разделяющей первую и вторую области, опускается ниже температуры замерзания воды, что соответствует «переохлаждению» воды. Следовательно, в этом случае модель с двумя подвижными межфазными границами не позволяет построить физически непротиворечивое решение. Для устранения данного противоречия необходимо вводить третью подвижную межфазную границу, на которой происходит образование льда, и соответственно дополнительно рассматривать четвертую область, в которой одновременно сосуществуют в состоянии фазового равновесия газ, лед и гидрат.
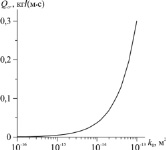
Рис. 2. Зависимость критического значения массового расхода от абсолютной проницаемости пласта: T0 = 275 К, p0 = 5 МПа
На рис. 2 изображена зависимость критического значения массового расхода отбора газа от абсолютной проницаемости, определяющего возникновение двух протяженных областей разложения гидрата как на газ и воду, так и на газ и лед. Данная кривая разделяет плоскость (k0, Q) на две области, каждая из которых соответствует различным режимам разложения гидрата. В области под кривой существует решение с разложением гидрата на газ и воду. Область выше кривой отвечает формированию двух протяженных областей фазовых переходов с разложением газогидрата как на газ и воду, так и на газ и лед. При этом в соответствии с рисунком режим с образованием льда характерен для низкопроницаемых пористых сред. Это обусловлено тем, что снижение проницаемости пласта при фиксированном массовом расходе отбора газа обуславливает значительное снижение давления непосредственно вблизи скважины, тем самым приводя к уменьшению давления и соответственно температуры на границе разложения гидрата ниже температуры замерзания воды.
Выводы
В работе исследованы особенности разложения газогидрата в пористой среде при отборе газа. Показано, что в зависимости от интенсивности отбора газа и исходных параметров системы разложение газогидрата может происходить либо на газ и воду, либо как на газ и воду, так и на газ и лед.
Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта 14-01-31089 мол_а.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор, декан физико-математического факультета Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор, заведующий кафедрой «Алгебра, геометрия и методика обучения математике» Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак.
Работа поступила в редакцию 01.04.2015.
Библиографическая ссылка
Хасанов М.К., Доровская М.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОТБОРА ГАЗА ИЗ ГАЗОГИДРАТНОГО ПЛАСТА С УЧЕТОМ ОБРАЗОВАНИЯ ЛЬДА // Фундаментальные исследования. – 2015. – № 2-13. – С. 2846-2850;URL: https://fundamental-research.ru/ru/article/view?id=37572 (дата обращения: 20.04.2024).