Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кротов Е.А. 1 Терентьев А.В. 1

---

1 СПбГМТУ «Санкт-Петербургский государственный морской технический университет»

Проведен анализ различных форм тонких осесимметричных оболочек вращения при разных граничных условиях с целью нахождения функций перемещений, удовлетворяющих условиям закрепления. Учитывалась нелинейная взаимосвязь между перемещениями и деформациями, соответствующая нелинейной теории. Построены базисные функции, удовлетворяющие граничным условиям как для перемещений и усилий, так и для их линейных комбинаций. Рассмотрены замкнутая и незамкнутая в вершине оболочки вращения. Полученные базисные функции представляют полиномиальную зависимость от координат. Базисные функции не ортогональны, но обладают свойством полноты и построены в виде, который позволяет производить не только численное, но и аналитическое интегрирование, то есть можно рекомендовать эти функции для решения задач теории оболочек с использованием метода Бубнова-Галеркина.

Статья в формате PDF

1800 KB

базисные функции

нелинейная теория

метод Бубнова-Галёркина

замкнутая и незамкнутая в вершине оболочка вращения

1. Ворович И.И., Минакова Н.И. Устойчивость непологого сферического купола // Прикладная математика и механика, 1968. – № 2. – C. 332–338.

2. Жилин П.А. Прикладная механика. Основы теории оболочек. – СПб.: Изд-во Политехнического университета, 2006. – 167 с.

3. Ивлев В.В. Математический анализ. Функции многих переменных. – М.: Икар, 2013. – 548 с.

4. Флетчер К. Численные методы на основе метода Галёркина. – М.: Мир, 1988. – 353 с.

5. Шаповалов Л.А. Об одном простейшем варианте уравнений геометрически нелинейной теории тонких оболочек // Механика твердого тела. – 1968. – № 1. – С. 56–62.

Основным требованием, предъявляемым к численному методу исследования конкретной конструкции, является оптимальное сочетание ее простоты (наглядности, простоты реализации и т.п.) и эффективности (достижения хорошей точности при возможно меньших затратах вычислительного времени). То есть везде, где это возможно, надо использовать более простой метод [1].

Оболочки вращения, используемые в машиностроении, обладают той особенностью, что в основном образующая их имеет плавные очертания, и они подвержены действию плавной нагрузки. В этих условиях может быть эффективен метод Бубнова-Галеркина, который описан в [4] и используется для анализа деформации ряда конкретных оболочек.

Основным препятствием для применения метода Бубнова-Галеркина в геометрически нелинейных задачах теории тонких оболочек [2] является необходимость подбора базисных функций, удовлетворяющих нелинейным граничным условиям.

Остановимся на формулировке возможных типов граничных условий для оболочек вращения, которые первоначально были представлены в [1]. Поскольку система уравнений в неизвестных перемещениях w и t = R1θ1 = u – w´, (здесь u и w – тангенциальное и нормальное перемещения соответственно, R1 – радиус кривизны, θ1 – угол поворота) имеет шестой порядок, то необходимо иметь шесть граничных условий.

На контурах оболочки должны быть заданы величины u или T1 (тангенциальное усилие) и w или N1 (поперечное усилие) и θ1 или M1 (изгибающий момент) (если контур один, то используется условие симметричности при равенстве нулю угла поворота касательной к координатной линии θ = 0). Каждый из этих шести параметров должен либо равняться нулю, либо иметь конечное значение, либо может выражаться через соответствующее перемещение. Поэтому на одном контуре оболочки в общем случае может быть осуществлен один из 27 типов условий:

u = В∙T1 (В = 0, В, ∞)

w = A∙N1 (A = 0, A, ∞)

θ1 = ℘∙M1 (℘ = 0, ℘, ∞). (1)

При этом первое условие из (1) A = 0, B = 0, ℘ = 0 отвечает условию симметричности относительно оси θ = 0 для замкнутой в вершине оболочки вращения.

В общем случае на границе могут быть заданы не сами перемещения u и w, усилия T1 и N1, а их линейные комбинации. Покажем, что в этом случае задача отыскания базисных функций будет также сведена к нахождению их для указанных 27 условий или их комбинаций.

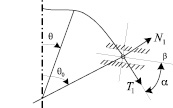
Направления внутренних усилий в точке с координатой θ0

Допустим, что граничные условия выписаны согласно рисунку для линейных комбинаций усилий и перемещений, т.е. для величин

,

,

,

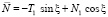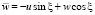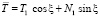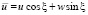. (2)

где ξ = ξ(ρ) – угол между касательной к срединной поверхности оболочки в данной точке и прямой β:

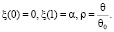(3)

Считаем, что функции, удовлетворяющие условиям для функций 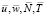, получены (это условия (1)). Тогда, считая T1, N1, u, w за неизвестные функции, найдем их из (2):

,

,

,

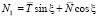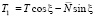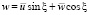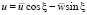. (4)

Таким образом, отыскание базисных функций для случая, когда граничные условия заданы линейной комбинацией u и w, N1 и T1, сводится к отысканию этих функций для условий (1).

Если получение функции ξ = ξ(ρ), входящей в (4) в качестве аргумента тригонометрической функции, по каким-либо причинам затруднительно, то можно применять:

а) для замкнутой в вершине оболочки вращения следующее выражение:

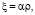(5)

поскольку условия (3) тогда будут выполнены,

б) для незамкнутой в вершине оболочки, имеющей два контура, ξ(ρ0) = α0

.

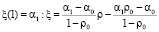Итак, для всего многообразия граничных условий достаточно иметь базисные функции для 27 случаев (1) при рассмотрении замкнутой в вершине оболочки, и 351 (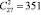) случаев для незамкнутой в вершине оболочки.

Для решения задачи методом Бубнова-Галеркина функции u, w и t представим в следующем виде:

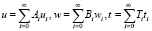. (6)

Дальнейшая цель работы заключается в подборе ui, wi, ti для различных типов закрепления края в случае осесимметричного нагружения оболочки вращения с учётом нелинейной связи между деформациями и перемещениями, предложенной Л.А. Шаповаловым в [5].

Подбор функций ui, wi, ti гораздо проще осуществляется для замкнутой в вершине оболочки вращения (типа купола), имеющей один граничный контур, чем для оболочки незамкнутой с двумя граничными контурами. Это связано с тем, что удовлетворить условиям симметричности (в первом случае) при ρ = 0 проще, чем на границе (во втором) при фиксированном конечном значении координаты ρ = ρ0. В связи с этим рассмотрим два случая.

Замкнутая в вершине оболочка вращения

1. Для всех видов закрепления опорного контура такой оболочки базисные функции должны удовлетворять одним и тем же условиям симметричности (при ρ = 0):

u = 0, t = 0, N1 = 0. (7)

При этом третье из условий (7) в перемещениях принимает вид

t´´ = 0 при ρ = 0. (8)

Условие (8) получается после записи выражения для поперечного усилия N1

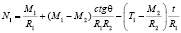(9)

и нахождения 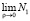с применением правила Лопиталя, описанного в [3] для неопределённостей .

2. Рассмотрим оболочку, имеющую следующее закрепление опорного контура (при ρ = 1):

u = 0, N1 = w/A, M1 = t/℘R1,

w ≠ 0, t ≠ 0. (10)

Третье из условий (10) после подстановки выражения для M1 и ряда преобразований принимает вид

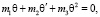(11)

где

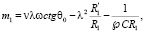
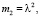
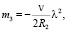
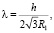
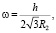
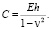(12)

Здесь h – толщина оболочки; E – модуль Юнга, v – коэффициент Пуассона.

Второе условие (10) после подстановки выражений для усилий и несложных преобразований принимает вид

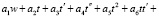
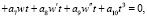(13)

где

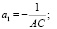
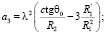
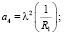
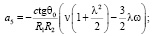
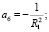
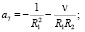
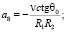
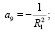
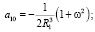
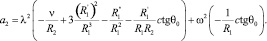(14)

Будем искать выражения для функций wi и θi в виде

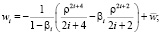
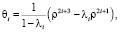
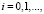(15)

где λi, βi, 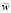– константы.

Легко убедиться непосредственной подстановкой, что функции (15) удовлетворяют всем условиям симметричности (условие 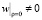накладывает лишь ограничение на 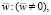а также граничным условиям u = 0, t ≠ 0 при ρ = 1 (условие 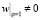накладывает ограничение на ).

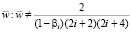Остаётся убедиться, что существуют значения λi и βi, отличные от 1, при которых и условия (11) и (13) были бы удовлетворены. После подстановки (15) в (11) и (13) и преобразований, получаем

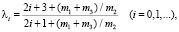
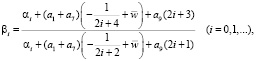(16)

где

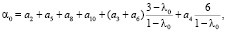
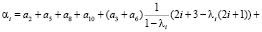
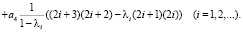(17)

В общем случае, λi и βi отличны от 1, значит, функции (15) удовлетворяют всем граничным условиям и действительно являются искомыми.

3. Рассмотрим ряд важных частных случаев, имеющих предельный для A и ℘ характер.

a) A = 0. Тогда a1 = –1/(AC) → ∞ при ρ → 1, а

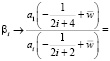
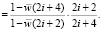(18)

Решение в функциях (15) существует.

б) A = ∞. В этом случае a1 = 0. Подставляя a1 в (17), находим βi. Решение существует.

в) ℘ = ∞. Тогда 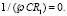Подставляя это выражение в (12), получим m1. Решение существует.

г) ℘ = 0. Тогда m1 =∞, 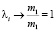при ρ → 1, а ti → ∞. Неприводимый случай. Использовать для него функции (15) нельзя.

4. Рассмотрим ещё два важных случая закрепления граничного контура оболочки, замкнутой в вершине.

4.1. Пусть мы имеем абсолютно жёсткую заделку, то есть при ρ = 1

u = 0, w = 0, t = 0. (19)

Можно решать эту задачу, используя следующие базисные функции:

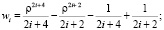
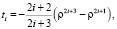
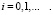(20)

В том, что они удовлетворяют всем граничным условиям, легко убедиться непосредственной подстановкой.

4.2. Пусть мы имеем закрепление типа «скользящей заделки», т.е. при ρ = 1

w = 0, t = 0, T1 = 0, u ≠ 0. (21)

Третье условие (21) эквивалентно следующему:

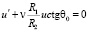при ρ = 1. (22)

Эту задачу можно решать, используя следующие базисные функции:

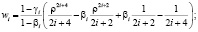
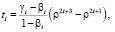
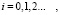(23)

где

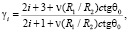
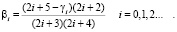
Функции (23) удовлетворяют всем условиям (21), (22) и (7), (8).

Незамкнутая в вершине оболочка вращения

Приведём здесь результаты лишь для одного варианта закрепления, а именно:

при ρ = ρ0(0 < ρ0 < 1) и ρ = 1:

w = 0, t = 0, T1 = 0, u ≠ 0. (24)

Можно решать эту задачу, используя следующие базисные функции:

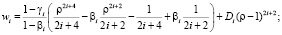
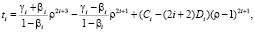(25)

где

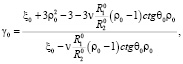
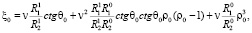
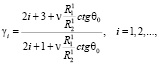(26)

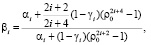
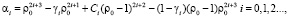
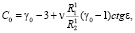
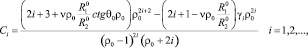
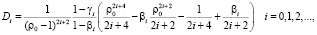
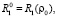
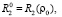
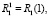
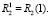
Функции (25) удовлетворяют всем граничным условиям (24).

Выводы

Все предложенные базисные функции представляют собой полиномы различных степеней. Система функций обладает свойством полноты, поскольку функции линейно независимы из-за различных степеней полиномов. Функции не ортогональны, но интегралы от них и их произведений не обладают никакими особенностями, просты и легко берутся как аналитически, так и численно. В силу этого можно рекомендовать эти функции для решения задач теории оболочек с использованием метода Бубнова-Галеркина.

Рецензенты:

Картузов Е.И., д.т.н., профессор кафедры теоретической механики Санкт-Петербургского государственного морского технического университета, г. Санкт-Петербург;

Сорокин С.В., д.т.н., профессор кафедры сопротивления материалов Санкт-Петербургского государственного морского технического университета, г. Санкт-Петербург.

Работа поступила в редакцию 01.04.2015.

Библиографическая ссылка