Существующие на данный момент программно-алгоритмические комплексы прогнозирования технического состояния бортовой аппаратуры космических аппаратов обладают рядом недостатков, описанных в [2, 4, 6]. В работах [1, ,2] проанализированы особенности существующего подхода и рассмотрена задача обоснования нечётких значений границ поля допуска (ГПД) параметров ТС БА КА в условиях неопределённой информации о внешних воздействиях среды, в том числе на стадии создания КА. В данной статье предложен способ преобразования нечётких границ поля допуска к чётким с использованием дополнительной информации о цене отказа элемента БА КА по рассматриваемому параметру.
Цель исследования
Математический аппарат теории нечётких множеств [3] позволяет реализовать оценивание функций принадлежности границ поля допуска параметров БА КА непосредственно экспертным методом. Это даёт возможность преодолеть принципиальные трудности, связанные с отсутствием информации о точном числе факторов условий эксплуатации, а также с затруднённой количественной оценкой некоторых факторов [5]. Однако представление решения задачи прогнозирования момента отказа элемента БА КА в форме нечёткого множества имеет смысл, когда такая форма содержательно понятна лицу, принимающему решение по результатам прогнозирования по управлению ТС БА КА. В подавляющем большинстве практических задач, характерных для стадии эксплуатации КА, необходимо знание момента отказа элемента в чёткой (фиксированной) форме. Это обусловливает необходимость осуществления перехода к чётким значениям ГПД параметров на этапе создания КА.
Материалы и методы исследования
Исследуем особенности процесса прогнозирования технического состояния (ТС) бортовой аппаратуры космических аппаратов (БА КА) при следующих исходных допущениях:
– ТС элемента характеризуется одним выходным параметром х;
– информация об изменении ТС представлена единственной реализацией x(t) случайного процесса 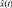 изменения выходного параметра;
изменения выходного параметра;
– поле допуска параметра х – одностороннее, с верхней (для определённости) границей, заданной в нечёткой форме (нечётким множеством 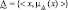 );
);
– реализация случайного процесса 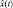 монотонная.
монотонная.
Обозначим 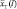 ,
, 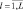 результат прогноза реализации x(t), известной до момента Т, с упреждением l. Если
результат прогноза реализации x(t), известной до момента Т, с упреждением l. Если 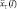 рассматривать как функцию упреждения прогноза l, то
рассматривать как функцию упреждения прогноза l, то 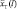 является прогнозирующей функцией.
является прогнозирующей функцией.
Для определения момента отказа элемента БА КА решим относительно l уравнение
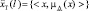 . (1)
. (1)
Обозначив 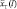 = f(l), получим
= f(l), получим
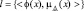 ,
,
где j(x) = f–1(l) – функция обратная f(l).
Следовательно, момент отказа элемента tотк определяется как
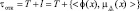 .
.
Согласно правилу сложения нечётких чисел [66], имеем:
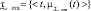 , (2)
, (2)
где t = T + j(x), 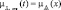 .
.
Таким образом, при нечётко определённой границе поля допуска (ГПД) параметра х, момент отказа элемента tотк есть нечёткое множество на оси времени с функцией принадлежности 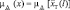 . На рис. 1 показано определение момента отказа в случае монотонного изменения реализации случайного процесса
. На рис. 1 показано определение момента отказа в случае монотонного изменения реализации случайного процесса 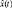 . Функция принадлежности НМ
. Функция принадлежности НМ  , как видно из рис. 1, является унимодальной.
, как видно из рис. 1, является унимодальной.
Если снять ограничение, касающееся монотонности изменения реализации случайного процесса 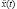 , то функция принадлежности НМ
, то функция принадлежности НМ  будет, как показано на рис. 2, полимодальной (имеющей несколько локальных экстремумов). При этом
будет, как показано на рис. 2, полимодальной (имеющей несколько локальных экстремумов). При этом
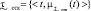 ,
,
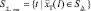 ,
,
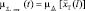 ,
,
где  и
и 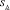 – носители НМ
– носители НМ  и
и  соответственно.
соответственно.
Результаты исследования и их обсуждение
Представление решения задачи прогнозирования момента отказа элемента в форме нечёткого множества имеет смысл, когда такая форма содержательно понятна лицу, принимающему решение по результатам прогнозирования по управлению ТС БА КА. Однако в подавляющем большинстве практических задач, характерных для этапа эксплуатации КА, необходимо знание момента отказа элемента в чёткой (фиксированной) форме. Это обусловливает необходимость осуществления дополнительных операций по «стягиванию» нечёткого множества  в точку на временной оси. Для этих целей может быть использована дополнительная информация по отношению к имевшейся ранее при определении нечёткого множества
в точку на временной оси. Для этих целей может быть использована дополнительная информация по отношению к имевшейся ранее при определении нечёткого множества 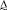 ГПД. Одним из таких способов является следующий:
ГПД. Одним из таких способов является следующий:
– определяется чёткое множество a-уровня НМ 
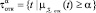 , (3)
, (3)
– находится чёткое значение момента отказа tотк как
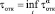 . (4)
. (4)
В качестве дополнительной информации при определении значения уровня a целесообразно использовать информацию о цене отказа элемента БА КА bx по рассматриваемому параметру х. При этом очевидно, что a и bx должны быть связаны некоторой функциональной зависимостью a = g(bx). Функция g является монотонно убывающей.
Положительной стороной изложенного подхода к определению фиксированного момента отказа БА КА является возможность учёта дополнительной информации, имеющейся непосредственно в момент прогнозирования. Так как КА представляют собой сложные многофункциональные объекты, цена отказа элементов которых определяется важностью решаемой задачи и соответственно изменяется во времени, то критерий определения значения tотк на основе (3) и (4) является наиболее гибким с точки зрения учёта специфики функционирования БА КА в реальном масштабе времени.
Однако практическая реализация данного критерия фиксации момента отказа осложняется необходимостью определения значения bx цены отказа элемента по параметру х методом экспертного оценивания, что не всегда является возможным ввиду отсутствия достаточного количества компетентных экспертов в момент прогнозирования ТС, кроме того существуют определённые трудности в выборе конкретного типа функции g(bx). Необходимость выполнения описанных операций наряду с непосредственным прогнозированием реализации x(t) увеличивает общее время прогнозирования момента отказа элемента БА КА, что отрицательно сказывается на готовности КА в целом.
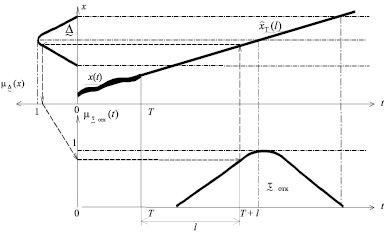
Рис. 1. Определение момента отказа в случае монотонного изменения реализации x(t) случайного процесса 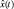 и нечётко определённой верхней ГПД
и нечётко определённой верхней ГПД 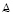

Рис. 2. Определение момента отказа в случае немонотонного изменения реализации x(t) случайного процесса 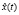 и нечётко определённой верхней ГПД
и нечётко определённой верхней ГПД 
Использование данного подхода на практике предполагает задание ГПД параметра х в нечёткой форме для всего периода эксплуатации. Это значительно усложняет процедуру контроля ТС, делает невозможным применение для этой цели существующих технических средств контроля и прогнозирования ТС, ориентированных на использование чётких ГПД.
Указанные недостатки обусловливают необходимость расчёта чётких значений ГПД параметров на этапе создания КА. Ввиду того, что информация об условиях эксплуатации БА КА на этапе создания ограничена, для повышения точности определения ГПД целесообразно по мере накопления подобной информации производить периодическую коррекцию их значений.
Задача оценивания чёткого значения границы поля допуска параметра элемента при ограниченном объёме информации об условиях эксплуатации может быть сформулирована следующим образом.
Пусть Х – универсальное множество альтернатив, т.е. универсальная совокупность всех возможных выборов лица, принимающего решения (ЛПР). Множество Х есть множество возможных значений параметра х. Задано нечёткое ограничение или множество допустимых альтернатив, описываемое нечётким подмножеством множества Х. Множество допустимых альтернатив есть нечёткое множество 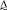 границы поля допуска параметра х. Задача принятия решений заключается при этом в выборе допустимой альтернативы (чёткого значения ГПД), которая лучше или не хуже всех остальных альтернатив в смысле заданного отношения предпочтения, отражающего интересы лица, принимающего решения.
границы поля допуска параметра х. Задача принятия решений заключается при этом в выборе допустимой альтернативы (чёткого значения ГПД), которая лучше или не хуже всех остальных альтернатив в смысле заданного отношения предпочтения, отражающего интересы лица, принимающего решения.
Рассмотрим отношение предпочтения в форме так называемой функции полезности, имеющей вид отображения множества альтернатив на числовую ось. Задачи принятия решения, в которых отношение предпочтения описано чётко в форме функции полезности, а нечёткость содержится в описании множества альтернатив, относятся к задачам нечёткого математического программирования (НМП).
Решение задачи НМП в относительно простой форме возможно на основании подхода Беллмана-Заде. Основным в данном подходе к решению рассматриваемой задачи является то, что цели принятия решений и множество альтернатив рассматриваются как равноправные нечёткие подмножества универсального множества альтернатив. Нечёткой целью в Х является нечёткое подмножество Х, которое будем обозначать 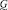 . Описывается нечёткая цель функцией принадлежности
. Описывается нечёткая цель функцией принадлежности 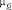 : Х → [0, 1].
: Х → [0, 1].
Нечётким решением задачи достижения нечёткой цели называется пересечение нечётких множеств цели и ограничений, т.е. функция принадлежности решения  имеет вид (рис. 3)
имеет вид (рис. 3)
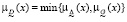 . (5)
. (5)
При наличии нескольких целей нечёткое решение описывается функцией принадлежности
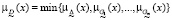 . (6)
. (6)
Если различные цели различаются по важности и заданы соответствующие коэффициенты относительной важности целей li, то ФП решения задачи определяется выражением
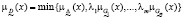 . (7)
. (7)
Заключение
Определённое таким образом решение можно рассматривать как нечётко сформулированную инструкцию, исполнение которой обеспечивает достижение нечётко поставленной цели. Нечёткость полученного решения  есть следствие нечёткости самой исходной задачи. При таком представлении решения остаётся неопределённость, связанная со способом исполнения подобной нечёткой инструкции, т.е. с тем, какую альтернативу выбрать. Различные способы разрешения этой неопределённости предлагаются, например, в работе Л. Заде [3].
есть следствие нечёткости самой исходной задачи. При таком представлении решения остаётся неопределённость, связанная со способом исполнения подобной нечёткой инструкции, т.е. с тем, какую альтернативу выбрать. Различные способы разрешения этой неопределённости предлагаются, например, в работе Л. Заде [3].
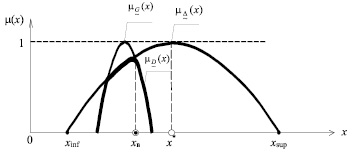
Рис. 3. Нечёткое решение задачи НМП на основании подхода Беллмана-Заде
Один из наиболее распространённых в литературе способов состоит в выборе альтернативы, имеющей максимальную степень принадлежности нечёткому решению, т.е. альтернативы, реализующей
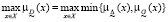 . (8)
. (8)
Такую альтернативу называют максимизирующим решением.
Задача выбора фиксированного значения границы поля допуска параметра х есть, таким образом, задача поиска максимизирующего решения (8) в задаче НМП.
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург;
Садин Д.В., д.т.н., профессор, профессор кафедры, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Работа поступила в редакцию 01.04.2015.
Библиографическая ссылка
Миронов Е.А., Миронов А.Н., Шестопалова О.Л., Платонов С.А. ОЦЕНИВАНИЕ ЗНАЧЕНИЙ ГРАНИЦ ПОЛЯ ДОПУСКА ПАРАМЕТРОВ БОРТОВОЙ АППАРАТУРЫ КОСМИЧЕСКИХ АППАРАТОВ ДЛЯ СТАДИИ ЭКСПЛУАТАЦИИ В УСЛОВИЯХ ИНФОРМАЦИОННОЙ НЕОПРЕДЕЛЁННОСТИ // Фундаментальные исследования. 2015. № 2-13. С. 2819-2823;URL: https://fundamental-research.ru/ru/article/view?id=37567 (дата обращения: 04.02.2026).



