К настоящему моменту времени установлено, что современные комплексы методического и алгоритмического обеспечения обработки результатов телеметрического контроля бортовой аппаратуры (БА) космических аппаратов (КА) обладают рядом ключевых недостатков, одним из которых является несовершенство методик назначения границ полей допусков (ГПД) на параметры технического состояния (ТС) БА КА, которые обычно задаются постоянными величинами, определяемыми по принципу наихудшего сочетания наиболее неблагоприятных факторов условий эксплуатации. Кроме того, недостаточно проработаны вопросы обоснования значений ГПД параметров ТС элементов и подсистем БА КА для ситуаций воздействия на КА естественных и преднамеренных факторов с уровнями, превышающими среднестатистические.
Цель исследования
В данной статье представлено обоснование нечёткого подхода к определению ГПД параметров ТС БА КА на этапе проектирования и эксплуатации. Границы области работоспособности БА КА предложено описывать нечёткими множествами, функции принадлежности которых оцениваются на основе формализованного представления опыта экспертов с помощью нечетких лингвистических шкал. Это позволит при прогнозировании надежности и живучести КА учесть априорную информацию о степени влияния факторов неблагоприятных воздействий на БА КА.
Материалы и методы исследования
Пусть качество выполнения заданных функций БА КА оценивается некоторым скалярным показателем качества функционирования Ккф. Задано пороговое значение 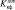 , относительно которого справедливо следующее утверждение: если выполнено условие
, относительно которого справедливо следующее утверждение: если выполнено условие
Ккф ≥ 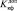 , (1)
, (1)
элемент БА находится в работоспособном состоянии, в противном случае он неработоспособен. В общем случае задача прогнозирования ТС в широком смысле сводится к предсказанию в будущие моменты или интервалы времени различных показателей качества элемента БА КА, связанных с моментом нарушения выполнения условия (1). Назовём событие, заключающееся в нарушении условия (1), отказом элемента в широком смысле, а состояние элемента, при котором условие (1) выполнено, соответственно работоспособным состоянием в широком смысле.
Основная трудность в применении такого подхода в задачах анализа параметрической надёжности заключается в том, что показатель качества функционирования Ккф невозможно, как правило, непосредственно измерить в процессе эксплуатации БА КА. Возникает необходимость найти способ проверки выполнения условия (1), не вычисляя значение Ккф. Одним из способов решения этой задачи является следующий.
Необходимо найти такой показатель r, который связан с Ккф известной (доступной определению) однозначной зависимостью и, кроме того, является наблюдаемым, т.е. измеримым в процессе испытаний (эксплуатации). Определив Р доп как область значений этого показателя, для которых выполняется условие (1), можно сформулировать правило определения работоспособности элемента БА КА в виде условия:
(Kкф ≥ 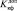 ) ⇔ (r ∈ Pдоп). (2)
) ⇔ (r ∈ Pдоп). (2)
В качестве показателя r на практике целесообразно использовать вектор выходных параметров элемента Х<n>, удовлетворяющий требованию наблюдаемости. Значения вектора Х<n>, как известно, в каждый момент времени определяют техническое состояние БА КА. Однако, знания ТС элемента в такой трактовке, в общем случае, недостаточно для определения его работоспособности.
В задаче определения работоспособности [2, 3] всегда присутствуют два момента. Первый связан с описанием и определением технического состояния элемента, т.е. значений вектора Х<n>. Второй учитывает качество работы элемента при данном состоянии. Качество функционирования элемента БА КА зависит от состояния элемента и состояния среды функционирования. Обозначив данные состояния соответственно S(0) и S(с) , можно записать
Ккф = f (S (0) , S(c) ). (3)
Состояние элемента S(0) определяется совокупностью значений его выходных параметров
S (0) = X<n> = <x1, x2,…, xn>, (4)
т.е. точкой в пространстве Rn. Состояние среды функционирования элемента S(c) обусловливается совокупностью условий эксплуатации и представляет собой т-мерный вектор
S(c) = X<m> = <x1, x2,…, xm>, (5)
где xi, 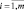 – значение i-го фактора условий эксплуатации элемента. Таким образом, f есть некоторая функция векторов S(0) и S(c).
– значение i-го фактора условий эксплуатации элемента. Таким образом, f есть некоторая функция векторов S(0) и S(c).
Для использования вектора X<n> в качестве показателя r в выражении (2) необходимо обеспечить однозначность отображения множества значений вектора S(0) на множество значений Ккф в моменты оценивания ТС или на интервале упреждения при прогнозировании ТС. Это означает, что аргумент S(с) в функции (5.2) должен быть зафиксирован. Допустим, что существует возможность предсказания изменения вектора S(с) на интервале времени Tупр. Обозначим результат такого прогноза 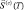 или
или 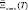 . Тогда выражение (5.3) запишется в виде
. Тогда выражение (5.3) запишется в виде
Kкф = f 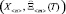 . (6)
. (6)
Подставив формулу (5.6) в левую часть (5.1), получим:
f 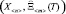 ≥
≥ 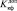 . (7)
. (7)
Множество значений вектора X<n> , удовлетворяющих условию (7), образуют в пространстве Rn некоторую связную область 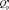 , называемую областью работоспособных состояний элемента БА КА (областью работоспособности). Критерием работоспособности элемента при этом является нахождение вектора X<n> в области
, называемую областью работоспособных состояний элемента БА КА (областью работоспособности). Критерием работоспособности элемента при этом является нахождение вектора X<n> в области 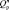
X<n> ∈ 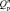 | S(c) =
| S(c) = 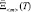 , Т ∈ [0, Tупр], (8)
, Т ∈ [0, Tупр], (8)
при условии известной функции изменения состояния среды функционирования на интервале Tупр. Данный критерий положен в основу определения работоспособности элемента БА КА в узком смысле, т.е. при некоторых сделанных допущениях о состоянии среды функционирования [5].
Область работоспособности 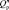 принадлежит более широкой области устойчивого функционирования
принадлежит более широкой области устойчивого функционирования 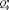 . Областью устойчивого функционирования называется область изменения величин параметров xi,
. Областью устойчивого функционирования называется область изменения величин параметров xi, 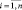 , при которых не нарушается свойство функционирования элемента [1]. Условие устойчивого функционирования элемента можно записать
, при которых не нарушается свойство функционирования элемента [1]. Условие устойчивого функционирования элемента можно записать
f 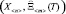 > 0. (9)
> 0. (9)
В соответствии с приведённым выше определением работоспособности элемента в узком смысле, отказом элемента БА КА в узком смысле является событие, заключающееся в нарушении условия (7). Это определение эквивалентно принятому в ГОСТ 27.002-89.
Для проверки выполнения условия (7) необходимо определить границы 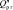 области работоспособности
области работоспособности 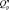 . Для этого приравняем левую и правую части неравенства (7) и решим полученное уравнение
. Для этого приравняем левую и правую части неравенства (7) и решим полученное уравнение
f 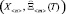 =
= 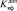
относительно X<n>:
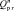 = j
= j 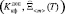 , (10)
, (10)
где j 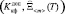 = f –1
= f –1 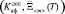 .
.
Анализируя выражение (10), можно сделать вывод о зависимости границ области работоспособности от изменения условий эксплуатации элемента. Можно выделить два основных подхода к определению границ области работоспособности: стохастический и детерминированный. Сущность стохастического подхода заключается в описании изменения условий эксплуатации элемента вектором случайных функций:
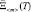 =
= 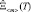 . (11)
. (11)
Границы области работоспособности 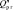 с учётом (5.11) определяются как случайная функция, изменяющаяся в пространстве R n
с учётом (5.11) определяются как случайная функция, изменяющаяся в пространстве R n
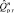 = j
= j 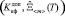 . (12)
. (12)
Стохастический подход к определению границ области работоспособности отражает реальный характер изменения 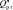 элемента БА КА в процессе эксплуатации, однако он обладает рядом недостатков:
элемента БА КА в процессе эксплуатации, однако он обладает рядом недостатков:
– существуют объективные трудности получения информации о вероятностных характеристиках элементов вектора условий эксплуатации 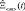 , обусловленные практической невозможностью контроля части факторов xi;
, обусловленные практической невозможностью контроля части факторов xi;
– вид функции f и соответственно j в формуле (10), как правило, определяется по результатам эксперимента, для осуществления которого необходимо достаточное время и средства;
– определение типа и параметров закона распределения границы области работоспособности непосредственно в эксперименте требует проведения специальных испытаний элемента БА КА в условиях нормального функционирования;
– затруднено получение выражений для расчёта показателей безотказности элемента при случайном характере допустимых границ изменения его параметров [4];
– при случайных допустимых границах изменения параметров элемента существенно усложняется задача контроля ТС в процессе эксплуатации из-за необходимости оценивания фактических значений реализаций случайного процесса изменения границы.
Недостатки рассмотренного подхода обусловили широкое распространение в задачах оценивания и прогнозирования ТС детерминированного подхода к определению допустимых границ изменения параметров БА КА.
Основой детерминированного подхода является расчёт границ области работоспособности для ситуации, в которой факторы условий эксплуатации воздействуют на качество функционирования БА КА максимально неблагоприятно. Данный подход в литературе иначе называется минимаксным. При этом
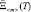 =
= 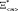 , (13)
, (13)
где 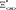 – вектор параметров условий эксплуатации, наиболее неблагоприятно из всех возможных векторов влияющий на качество функционирования элемента.
– вектор параметров условий эксплуатации, наиболее неблагоприятно из всех возможных векторов влияющий на качество функционирования элемента.
Подставив 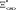 в (7), получим условие работоспособности элемента СВТС при максимально неблагоприятных условиях эксплуатации:
в (7), получим условие работоспособности элемента СВТС при максимально неблагоприятных условиях эксплуатации:
f  ≥
≥ 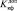 . (14)
. (14)
Множество значений вектора X<n> , удовлетворяющих условию (14), образуют в пространстве Rn некоторую область 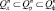 , называемую допустимой областью изменения параметров элемента. Для большинства реальных элементов БА КА характерным свойством является криволинейность границ областей
, называемую допустимой областью изменения параметров элемента. Для большинства реальных элементов БА КА характерным свойством является криволинейность границ областей 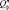 ,
, 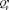 и
и  , обусловленная имеющимся в общем случае свойством аддитивности влияния изменения элементов вектора X<n> на значение показателя качества функционирования Ккф.
, обусловленная имеющимся в общем случае свойством аддитивности влияния изменения элементов вектора X<n> на значение показателя качества функционирования Ккф.
Результаты исследования и их обсуждение
Стремление к упрощению процедур контроля и прогнозирования работоспособности элементов на этапе эксплуатации обусловило введение постоянных допустимых границ изменения параметров (допусковых границ).
Введение постоянных границ поля допуска при криволинейных границах области 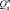 является задачей неординарной. Основой подхода к ее решению является аппроксимация криволинейной области
является задачей неординарной. Основой подхода к ее решению является аппроксимация криволинейной области 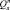 параллелепипедом (гипербрусом), проекции граней которого на координатные оси и дают значения границ поля допуска. Определение границ поля допуска на параметры элемента для двумерного случая показано на рисунке.
параллелепипедом (гипербрусом), проекции граней которого на координатные оси и дают значения границ поля допуска. Определение границ поля допуска на параметры элемента для двумерного случая показано на рисунке.
Преимуществами детерминированного подхода по сравнению со стохастическим являются: значительное упрощение процедуры контроля работоспособности БА КА, возможность задания независимых допусков на параметры, простота алгоритмической и аппаратурной реализации контроля и прогнозирования ТС. Однако эти преимущества получены ценой сужения области работоспособности при определении области 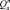 и её дальнейшей аппроксимации гипербрусом. Принимая во внимание то, что определение границ поля допуска на параметры элементов осуществляется на этапе создания КА, когда неопределённость информации об условиях эксплуатации велика, использование детерминированного подхода на практике зачастую приводит к чрезмерному сужению допустимых пределов изменения параметров элементов. Степень сужения области
и её дальнейшей аппроксимации гипербрусом. Принимая во внимание то, что определение границ поля допуска на параметры элементов осуществляется на этапе создания КА, когда неопределённость информации об условиях эксплуатации велика, использование детерминированного подхода на практике зачастую приводит к чрезмерному сужению допустимых пределов изменения параметров элементов. Степень сужения области 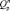 зависит от значения вектора
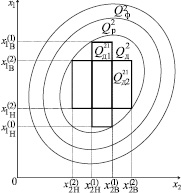
зависит от значения вектора  . Определение вектора
. Определение вектора 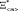 на практике, как правило, осуществляется эвристическими методами, результат применения которых во многом зависит от степени информированности разработчика КА об ожидаемых условиях эксплуатации элементов БА КА. Недостаточно обоснованное сужение границ поля допуска приводит на практике к возрастанию затрат времени и средств на регулирование параметров БА, что снижает готовность КА в целом.
на практике, как правило, осуществляется эвристическими методами, результат применения которых во многом зависит от степени информированности разработчика КА об ожидаемых условиях эксплуатации элементов БА КА. Недостаточно обоснованное сужение границ поля допуска приводит на практике к возрастанию затрат времени и средств на регулирование параметров БА, что снижает готовность КА в целом.
Указанные недостатки определяют необходимость разрешения противоречия между фактическим качеством функционирования элемента и существующими возможностями изменения программно-алгоритмического обеспечения и настройки аппаратного обеспечения КА, основанными на определении работоспособности в узком смысле.
Определение области работоспособности и границ поля допуска параметров элемента БА КА в двумерном случае
Заключение
Одним из направлений разрешения указанного противоречия является повышение обоснованности определения значения вектора 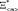 в условиях ограниченного объёма информации об условиях эксплуатации. Данная цель может быть достигнута решением следующих двух задач:
в условиях ограниченного объёма информации об условиях эксплуатации. Данная цель может быть достигнута решением следующих двух задач:
– расширением информационной базы принятия решения о значении вектора 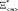 на этапе создания КА;
на этапе создания КА;
– корректированием значений границ поля допуска параметров элемента БА КА на этапе эксплуатации по мере накопления информации об её условиях.
Для решения этих задач целесообразно использовать информацию, содержащуюся в виде опыта и качественных представлений специалистов, разрабатывающих и эксплуатирующих КА. Принимая во внимание высокую степень неопределённости информации об условиях эксплуатации БА КА, исключающую возможность применения математического аппарата теории вероятности и математической статистики, а также нечёткость субъективных представлений, суждений специалистов-экспертов, целесообразно применить для априорного определения границ поля допуска параметров БА КА на стадии создания и эксплуатации математический аппарат теории нечётких множеств.
Рецензенты:
Козлов В.В., д.т.н., профессор, профессор кафедры, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург;
Садин Д.В., д.т.н., профессор, профессор кафедры, ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского» Министерства обороны РФ, г. Санкт-Петербург.
Работа поступила в редакцию 01.04.2015.
Библиографическая ссылка
Миронов А.Н., Миронов Е.А., Шестопалова О.Л., Платонов С.А. ИССЛЕДОВАНИЕ ВОПРОСОВ МОДЕЛИРОВАНИЯ ГРАНИЦ ОБЛАСТИ РАБОТОСПОСОБНОСТИ ЭЛЕМЕНТОВ БОРТОВОЙ АППАРАТУРЫ КОСМИЧЕСКИХ АППАРАТОВ НА СТАДИЯХ СОЗДАНИЯ И ЭКСПЛУАТАЦИИ // Фундаментальные исследования. 2015. № 2-13. С. 2815-2818;URL: https://fundamental-research.ru/ru/article/view?id=37566 (дата обращения: 12.03.2026).



