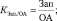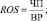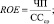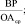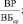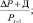Выбор направлений и стратегии развития, подготовка и принятие управленческих решений в рамках антикризисного менеджмента, направленных на обеспечение платёжеспособности предприятия корпоративного сектора экономики, обоснованно связываются с мониторингом и диагностикой перехода в состояние несостоятельности (банкротства).
На практике используются различные методы и модели оценки вероятности банкротства предприятия, основанные на анализе финансово-экономических показателей деятельности предприятия. Анализ динамики этих показателей с целью предсказания возможных осложнений в финансовой сфере корпораций проводился в США в 40–50-х гг., это связывалось с ростом числа банкротств в связи с сокращением военных заказов, неравномерностью развития отраслей и предприятий. В этих условиях возникла проблема априорного определения внешних и внутренних факторов и условий банкротства.
Известны следующие подходы к решению этой проблемы.
Количественный подход, основанный на анализе финансовых коэффициентов, реализован в моделях Е. Альтмана, У. Бивера, Р. Лиса, Г. Тисшоу, Р. Тоффлера, Д. Чессера и некоторых других учёных и исследователей-практиков. В моделях используются методы статистической обработки информации и дискриминантного анализа.
Качественный подход основан на сравнительном анализе показателей исследуемой компании и показателей обанкротившихся компаний. Реализован в моделях Дж. Аргенти и Т. Скоуна, в которых используются методы балльных оценок финансово-экономического состояния предприятий.
Первый исследователь, использовавший статистический анализ финансовых коэффициентов для прогнозирования банкротства предприятия, – У. Бивер [8], который разработал базу данных из 30 финансовых коэффициентов для модели статистического тестирования. Основным являлся коэффициент отношения потока платежей к величине задолженности. Средние значения этих показателей для финансово устойчивых компаний сравнивались с аналогичными для компаний, которые в дальнейшем обанкротились. Выяснилось, что среднее значение указанного коэффициента у компаний – кандидатов в банкроты значительно отличалось от значения этого показателя для компаний, сохранивших платёжеспособность.
Проведенные исследования позволили У. Биверу разработать пятифакторную модель оценки финансового состояния и диагностики банкротства предприятия. Использовались показатели: рентабельность активов, коэффициент долга, коэффициент текущей ликвидности, доля оборотного капитала в активах, коэффициент Бивера (отношение суммы чистой прибыли и амортизации к заёмным средствам). Полученные значения пяти показателей сравнивались с нормативными значениями, рассчитанными У. Бивером для трёх альтернатив: благополучные компании, компании, обанкротившиеся в течение года, компании, ставшие банкротами в течение пяти лет. Таким образом, весовые коэффициенты для показателей У. Бивером не использовались, а интегральный коэффициент вероятности банкротства не рассчитывался.
Впоследствии модель У. Бивера была усовершенствована с целью повышения точности прогноза банкротства предприятий для различных временных горизонтов. Наиболее простой является двухфакторная модель банкротства, использующая показатели текущей ликвидности Ктл и доли долга Кд. На основе статистической обработки данных по выборке фирм стран с рыночной экономикой выявлены весовые коэффициенты для каждого фактора. Для экономики США модель выглядит следующим образом [10]:
PR = –0,3877 – 1,0736·Kтл + 0,0579·Кд, (1)
Если PR ≥ 0,3, вероятность банкротства высокая; если –0,3 ≤ PR ≤ 0,3, вероятность банкротства средняя (если PR = 0, то вероятность банкротства равна 0,5); если PR < –0,3, вероятность банкротства низкая.
Исследование применимости рассмотренной модели для российских условий проведено М.А. Федотовой [3]. Автор справедливо указывает, что весовые коэффициенты следует уточнить для местных условий. Она также предлагает увеличить число учитываемых факторов за счёт показателя рентабельности активов.
Для повышения точности прогноза вероятности банкротства американскими аналитиками и финансовыми менеджерами широко используется известная пятифакторная модель Э. Альтмана («Z-score model»), коэффициент Z вероятности банкротства в которой рассчитывается на основе следующих показателей, веса которых устанавливаются на основе мультипликативного дискриминантного анализа [6]:
Z = 1,2X1 + 1,4X2 + 3,3X3 + 0,6X4 + X5, (2)
где Х1 – доля оборотного капитала в активах; Х2 – отношение накопленной прибыли к активам; Х3 – рентабельность активов; Х4 – отношение рыночной стоимости обычных и привилегированных акций к заёмным средствам[1]; Х5 – оборачиваемость активов.
В зависимости от значения Z проводится оценка вероятности банкротства на перспективу двух лет (табл. 1).
Таблица 1
Оценка вероятности банкротства по Z-критерию Э. Альтмана для предприятий США
|
Значение Z |
Вероятность банкротства |
|
Z < 1,81 |
Чрезвычайно высокая |
|
1,81 < Z < 2,675 |
Высокая |
|
Z = 2,675 |
Средняя |
|
2,675 < Z < 2,99 |
Низкая |
|
Z > 2,99 |
Сверхнизкая |
В общем случае плоскость (2) разделяет «успешные» и «неуспешные» предприятия, если известны (установлены) пороговые значения Z1 и Z2 критерия: Z < Z1 – вероятность банкротства компании высокая, Z > Z2 – вероятность банкротства низкая, Z1 < Z < Z2 – вероятность банкротства не определена.
Для компаний, акции которых не котируются на бирже, известен модифицированный четырёхфакторный вариант модели Э. Альтмана[2] [7]:
Z = 8,38X1 + X2 + 0,054X3 + 0,63X4, (3)
где Х4 – балансовая стоимость акций.
Широкое практическое применение имеют также модели Р. Таффлера и Г. Тишоу, Д. Чессера, Р. Лиса. Для экономики Великобритании Р. Таффлер и Г. Тишоу разработали следующий вариант Z-модели [11]:
Z = 0,53X1 + 0,13X2 + 0,18X3 + 0,16X4, (4)
где Х1 – отношение прибыли к краткосрочным обязательствам; Х2 – отношение оборотного капитала к величине пассивов; Х3 – отношение краткосрочных обязательств к величине пассивов; Х4 – отношение продаж к сумме активов.
При Z > 0,3 вероятность банкротства компании признается низкой.
Д. Чессер предложил следующую шестифакторную Z-модель оценки вероятности потери платежеспособности [9]:
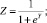
Y = –2,0434 – 5,24K1 + 0,0053K2 – 6,6507K3 + 4,4009K4 – 0,0791K5 – 0,102K6, (5)
где К1 – доля ликвидных активов; К2 – отношение суммы нетто-продаж к ликвидным активам; К3 – отношение брутто-доходов к совокупным активам; К4 – отношение общей задолженности к совокупным активам; К5 – отношение основного капитала к чистым активам; К6 – отношение оборотного капитала к объёму нетто-продаж.
Для идентификации банкротства Д. Чессер использовал следующие диапазоны Z-критерия: больше 0,5 – высокий риск невыполнения предприятием финансовых обязательств; меньше 0,5 – предприятие финансово устойчиво и платёжеспособно.
Модель Р. Лиса:
Z = 0,63X1 + 0,092X2 + 0,057X3 + 0,001X4, (6)
где Х1 – отношение оборотных активов к величине всех активов; Х2 – отношение накопленной прибыли к активам; Х3 – рентабельность активов; Х4 – отношение рыночной стоимости обычных и привилегированных акций к заёмным средствам.
При Z < 0,037 – вероятность банкротства высокая.
Следует отметить исследования в области прогнозирования банкротства, проведённые отечественными исследователями. Учёными Иркутской государственной экономической академии предложена четырёхфакторная модель оценки вероятности банкротства иркутских компаний (R-модель) [1]:
R = 8,38K1 + K2 + 0,054K3 + 0,63K4, (7)
где К1 – доля оборотных активов в совокупных активах; К2 – рентабельность капитала; К3 – оборачиваемость активов; К4 – рентабельность полных затрат.
Если R меньше 0, тогда вероятность банкротства выше 90 %, если R от 0 до 0,18, вероятность банкротства 60–70 %, если R от 0,18 до 0,32, вероятность банкротства 35–50 %, если R от 0,32 до 0,42, вероятность банкротства 15–20 %, если R больше 0,42, вероятность банкротства низкая.
Аргументированная критика рассмотренных выше n-факторных Z-моделей оценки вероятности банкротства предприятий включает как известные тезисы, часто приводимые различными авторами, так и собственные рассуждения авторов на эту тему. Отметим следующие.
1. Число и состав включаемых в Z-модель факторов – основной, если не главный объект критики статистических моделей Э. Альтмана и их модификаций.
Так, двух- и трёхфакторные модели не могут претендовать на точность прогноза. Однако с ростом числа оцениваемых факторов модели значительно усложняются. Они предполагают соответствующее программно–информационное обеспечение и сложны в использовании.
Далее, использование в Z-критерии Альтмана и в других моделях отношения рыночной стоимости обычных и привилегированных акций компании к объему заёмных средств (характеристика уровня покрытия обязательств собственным капиталом) вызывает справедливые вопросы в условиях неразвитости вторичного рынка российских ценных бумаг.
По этой причине специалисты Экспертного института Российского союза промышленников и предпринимателей предлагают руководствоваться Z-критерием Э. Альтмана без четвёртого фактора[3].
2. Z-критерий Э. Альтмана не отличается корректностью структуры: фактор Х1 оценивает качество управления, фактор Х4 характеризует финансовую сферу, в то время как остальные – экономическую. Таким образом, с позиции системного подхода Z-критерий не выдерживает критики.
Однако, в свою очередь, отметим, что эта критика не в полной мере необоснованна: существует определенная зависимость между динамическими рядами финансовых и экономических показателей «успешных» и испытывающих затруднения компаний, которая не зависит от их отраслевой принадлежности и однородности выборки. Важным в этом плане является фактор отличия исследуемой экономики от эффективной рыночной. Неучёт этого фактора и предполагает необходимость использования системного подхода.
3. Различия экономик, способов организации и ведения бизнеса в России и развитых странах оказывают значительное влияние как на состав используемых показателей, так и на их относительные веса, которые были Э. Альтманом рассчитаны на основе данных американской статистики 60–70 гг. прошлого века.
В связи с этим нельзя не согласиться, что эти веса не соответствуют современному состоянию и особенностям организации и ведения бизнеса в России, особенностям бухгалтерского и налогового учетов. Практическое отсутствие необходимой статистики по России мотивирует аналитиков использовать веса коэффициентов, определённые экспертным путем, что не обеспечивает достаточной точности прогноза.
Статистика, на которую опирались Э. Альтман и другие исследователи, возможно, и репрезентативна, но не обладает необходимым свойством статистической однородности выборки данных. В данном случае используются не выборки деталей из одной партии, а статистика предприятий, отличающихся организационно-технической и финансово-ресурсной спецификой, фазами жизненного цикла, уровнем менеджмента и пр. В этом случае нельзя говорить о статистической однородности событий, а следовательно, допустимость применения статистических методов ставится под сомнение. Таким образом, подход Э. Альтмана и его последователей был бы обоснован в условиях наличия однородности и репрезентативности событий банкротства.
4. Однако ключевой проблемой Z-метода является не проблема качества статистики. Дело в том, что классическая вероятность – характеристика не отдельного объекта или события, а генеральной совокупности событий. Рассматривая отдельный объект (предприятие), исследователь в терминах вероятности описывает его отношение к целой группе. Однако уникальность каждого предприятия заключается в том, что оно может выжить в неблагоприятных условиях (как, впрочем, и наоборот). В этом случае статистическая вероятность отсутствует.
Это наводит на мысль, что следует, во-первых, исследовать предприятия в отношении их совокупности, а не наоборот, а во-вторых, оценить внешние и внутренние условия предприятия с позиции «критичности» дистанции, отделяющей его от состояния банкротства.
Ответом на приведённую критику стали модели, основанные на рейтинговых оценках. Отметим модель рейтингового числа Р. Сайфуллина и Г. Кадыкова и шестифакторную модель О. Зайцевой. Рейтинговое число Р. Сайфуллина и Г. Кадыкова определяется следующим образом [5]:
R = 2Kc.c + 0,1 Kтл + 0,08Ко.а + 0,45Кр + Кс.к, (8)
где Кс.с – коэффициент обеспеченности собственными средствами; Ктл – коэффициент текущей ликвидности; Ко.а – коэффициент оборачиваемости активов; Кр – рентабельность продаж, Кс.к – рентабельность собственного капитала.
При полном соответствии финансовых коэффициентов нормативным уровням рейтинговое число равно единице и предприятие имеет удовлетворительное финансовое состояние. Финансовое состояние предприятий с рейтинговым числом, меньшим единицы, характеризуется как неудовлетворительное.
В шестифакторной модели О. Зайцевой [2] используются следующие показатели: Ку – коэффициент убыточности (отношение чистого убытка к собственному капиталу); Кз – соотношение кредиторской и дебиторской задолженностей; Кс – отношение краткосрочных обязательств к наиболее ликвидным активам; Куп – убыточность продукции (отношение чистого убытка к объему реализации продукции); Кр – финансовый рычаг (соотношение заёмного и собственного капиталов); Кз – коэффициент загрузки активов (величина, обратная коэффициенту оборачиваемости активов).
Коэффициент банкротства рассчитывается по формуле
К = 0,25Ку + 0,1Кз + 0,2Кс + + 0,25Куп + 0,1Кр + 0,1Кз. (9)
Весовые значения частных показателей в соотношении (9) определены экспертным путем. Фактический коэффициент банкротства сопоставляется с нормативным, рассчитанным на основе рекомендуемых нормативными документами пороговых значений частных показателей. Если фактический коэффициент больше нормативного, то вероятность банкротства велика, и наоборот.
Отметим, что весовые коэффициенты в модели О. Зайцевой определены без учета поправки на относительную величину значений частных коэффициентов. Так, нормативное значение показателя соотношения срочных обязательств и наиболее ликвидных активов равно семи, а нормативные значения коэффициента убыточности предприятия и коэффициента убыточности продукции равны нулю. По этой причине даже незначительные изменения первого показателя приводят к колебаниям итогового показателя, в десятки раз более сильным, чем изменения других показателей, при этом, по мысли автора модели, они, наоборот, должны иметь большие веса по сравнению с весом коэффициента отношения срочных обязательств и наиболее ликвидных активов.
Таким образом, основными объектами критики модели Э. Альтмана являются:
– недостаточная обоснованность выбора набора финансово-экономических показателей деятельности предприятия, значения которых определяют дистанцию современного его положения от положения «банкрот»;
– неучёт организационно-технических и финансово-ресурсных отличий предприятий одной отрасли, а тем более разных отраслей при формировании некоторого «усредненного» эталона, для которого на первом этапе определяется система весов показателей в Z-свёртке, а на втором – диапазон [Z1; Z2];
– «статичность» модели, заключающаяся в детерминированном характере процедур формирования набора весов показателей, а главное, диапазона [Z1, Z2], что не соответствует реалиям деятельности предприятий в условиях высокодинамичной рыночной среды.
Тем не менее идея метода Э. Альтмана весьма продуктивна и может быть использована для комплексной оценки финансово-экономического положения исследуемого предприятия (в нашем случае российского) с учётом следующих изменений.
Во-первых, следует отказаться от идеи формирования универсальной для всех предприятий Z-свёртки. Z-свёртка взвешенных значений привлекаемых показателей и оценочные интервалы её значений должны в полной мере отражать особенности рыночной деятельности исследуемого предприятия в конкретных условиях.
Во-вторых, необходимо максимально сузить объём используемой в модели субъективной информации сторонних экспертов, ограничив её только диапазонами изменений Z-коэффициента, разделяющих области отличного уровня устойчивости финансово-экономического состояния предприятия.
Рассмотрим модифицированный подход, реализующий основную идею метода Э. Альтмана, в основу которого положим перечисленные выше принципы формирования Z-свёртки финансовых коэффициентов, характеризующей финансово-экономическое положение не «усредненного», а конкретного предприятия.
В Z-свёртке будем использовать одиннадцать финансовых коэффициентов из предложенного Э.А. Хечумовой [4] универсального набора, дополненного коэффициентом «Совокупная доходность акций предприятия», позволяющим оценить инвестиционную привлекательность компании (влияющую на возможность расширения источников дополнительного финансирования). Расширенный универсальный набор финансовых коэффициентов представлен в табл. 2.
Для формирования набора весов {αi} коэффициентов в Z-свёртке, оценивающей финансово-экономическое состояние исследуемого предприятия в относительной шкале, задаваемой числами из интервала (0;1), используем следующие предпосылки и нормативно-справочную базу, характеризующую финансово-экономические результаты оптимальных по рыночному критерию вариантов деятельности предприятия для пессимистического и оптимистического сценариев развития его внешнего и внутреннего окружений.
1. Финансово-экономическое состояние предприятия оценивается в следующей качественной шкале: «значительно ниже удовлетворительного (критическое)», «ниже удовлетворительного (низкое)», «удовлетворительное», «выше удовлетворительного (стабильное)», «значительно выше удовлетворительного (превосходное)».
2. Перечисленным состояниям соответствуют экспертные оценки интервалов изменения интегрального показателя Z: для первого кластера – (0; R1], для второго – (R1, R2], для третьего – (R2, R3], для четвертого – (R3, R4], для пятого – (R4; 1). Примером набора диапазонов качественной оценки уровня финансово-экономического состояния предприятия может быть, например, следующий: (0; 0,5], (0,5; 0,72], (0,72; 0,86], (0,86; 0,95], (0,95; 1).
Таблица 2
Универсальный набор финансовых коэффициентов[4]
|
Наименование блока |
Наименование коэффициента |
Формула расчёта/расчётная база |
|
1 |
2 |
3 |
|
Финансовая устойчивость |
коэффициент автономии – x1 |
СС – собственные средства, ВБ – валюта баланса: СС = стр. 1300 + стр. 1530, ВБ = стр. 1600 |
|
коэффициент обеспеченности оборотных средств собственными источниками финансирования – x2 |
СС – собственные средства, ВА – внеоборотные активы, ОА – оборотные активы: СС = стр. 1300 + стр. 1530, ВА = стр. 1100, ОА = стр. 1200 |
|
|
коэффициент финансовой устойчивости – x3 |
ПК – перманентный капитал, ВБ – валюта баланса: ПК = стр. 1300 + стр. 1400 + стр. 1530, ВБ = стр. 1600 |
|
|
Ликвидность и платёжеспособность |
коэффициент абсолютной ликвидности – x4 |
стр. 1200 – КДЗ – стр. 1260 – ДДЗ – стр. 1220 – стр. 1210, стр. 1500 – стр. 1530 А1 = стр. 1240 + стр. 1250, П1 = стр. 1520, П2 = стр. 1510 + ЗУВД + стр. 1540 + стр. 1550 |
|
коэффициент быстрой ликвидности – x5 |
стр. 1200 – ДДЗ – стр. 1220 – стр. 1210 , стр. 1500 – стр. 1530 А2 = КДЗ |
|
|
коэффициент соотношения дебиторской и кредиторской задолженностей – x6 |
КЗ – кредиторская задолженность, КДЗ – краткосрочная дебиторская задолженность: КЗ = стр. 1520 |
|
|
доля запасов в текущих активах – x7 |
Зап – запасы, ОА – оборотные активы: Зап = стр. 1210 + стр. 1220, ОА = стр. 120. |
|
|
1 |
2 |
3 |
|
Рентабельность |
рентабельность продаж (по чистой прибыли) – x8 |
ЧП – чистая прибыль, ВР – выручка от реализации: ЧП = стр. 2400 (ф. № 2), ВР = стр. 2110 (ф. № 2) |
|
рентабельность собственных средств – x9 |
ЧП – чистая прибыль, ССср – средняя величина собственных средств за период: ЧП = стр. 2400 (ф. № 2), ССср = ср. значение (стр. 1300 + стр. 1530 (ф.№ 1)). |
|
|
Деловая активность |
оборачиваемость оборотных активов – x10 |
ВР – выручка от реализации, ОАср – средняя величина оборотных активов за период: ВР = стр. 2110 (ф. № 2). ОАср = ср. значение (стр. 1200 (ф. № 1)) |
|
оборачиваемость внеоборотных активов – x11 |
ВР – выручка от реализации, ВБср – средняя величина валюты баланса за период: ВБср = ср. значение (стр. 1600 (ф. № 1)) |
|
|
Инвестиционная привлекательность |
Совокупная доходность акций – x12 |
ΔP – прирост стоимости акций, Д – выплаченные дивиденды, Pt–1 – рыночная стоимость акции на начало периода |
3. Для каждой пары соседних диапазонов, характеризующейся «точкой перехода» Rj, определяется соответствующий набор {xji} 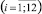 значений показателей универсального набора. Причем для первой и четвёртой пар диапазонов значения показателей наборов {x1,i} и {x4,i}
значений показателей универсального набора. Причем для первой и четвёртой пар диапазонов значения показателей наборов {x1,i} и {x4,i} 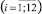 рассчитываются в соответствии с алгоритмом, приведённым на основе статей прогнозного баланса, соответствующих оптимальным вариантам деятельности предприятия для пессимистического и оптимистического сценариев развития его внешнего и внутреннего окружений. Для второй и третьей пар диапазонов (границы которых соответствуют значениям Z-свёртки, равным R2 и R3) «переходные» состояния баланса предприятия определяются на основе экспертных оценок и далее по приведённому в работе алгоритму определяются соответствующие наборы {x2i} и {x3i}
рассчитываются в соответствии с алгоритмом, приведённым на основе статей прогнозного баланса, соответствующих оптимальным вариантам деятельности предприятия для пессимистического и оптимистического сценариев развития его внешнего и внутреннего окружений. Для второй и третьей пар диапазонов (границы которых соответствуют значениям Z-свёртки, равным R2 и R3) «переходные» состояния баланса предприятия определяются на основе экспертных оценок и далее по приведённому в работе алгоритму определяются соответствующие наборы {x2i} и {x3i} 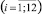 значений показателей универсального набора.
значений показателей универсального набора.
4. Для каждого из 12 финансовых коэффициентов, приведённых в табл. 2, определяется диапазон [0; bi] (или [0; ∞)) возможных его значений[5], который, в свою очередь, может быть разбит на интервалы, для каждого из которых известен характер монотонной зависимости значения Z-свёртки (1) от изменения соответствующего коэффициента в границах этого интервала: либо Z растёт с увеличением коэффициента xi, либо, наоборот, снижается (в первом случае рост i-го показателя характеризует улучшение финансово-экономического положения предприятия и укрепление финансовой устойчивости его рыночной деятельности, во втором – ухудшение положения и снижение финансовой устойчивости).
5. Пусть анализируемое значение xi i-го коэффициента попадает в интервал [bi,k; bi,k+1] с известным характером монотонной зависимости Z-свёртки от направления его изменения, причем bi,k ≠ 0, а bi,k+1 ≠ ∞ (крайние случаи рассмотрим ниже).
Со значением xi i-го коэффициента свяжем значение вновь вводимой переменной yi, рассчитываемое по следующим правилам.
Если в этом интервале значение Z-свёртки растет с ростом xi, то
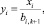 (10)
(10)
если – снижается, то
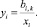 (11)
(11)
Если bi,k = 0 или bi,k+1 = ∞, то yi = 0[6].
Последнее правило в совокупности с правилами (10) и (11) гарантируют, что, во-первых, yi ∈ [0, 1], а, во-вторых, с ростом значения i-го показателя характер поведения Z-свертки переменных {yi} универсального набора
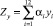 (12)
(12)
является монотонно-возрастающим по переменным yi (значения которых соответствуют значениям переменных xi из рассматриваемых интервалов), что в совокупности обеспечивает выполнение условия Zy ∈ (0,1), если сумма весов αi в Z-свёртке (12) не больше 1.
В терминах вновь введённых переменных yi наборам {x1,i}, {x2,i}, {x3,i}, {x4,i} соответствуют наборы {y1,i}, {y2,i}, {y3,i}, {y4,i}.
Рассмотрим следующую задачу линейного программирования:
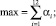 (13)
(13)
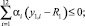 (14)
(14)
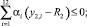 (15)
(15)
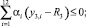 (16)
(16)
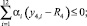 (17)
(17)
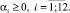 (18)
(18)
Если набор весовых коэффициентов 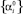 – её оптимальное решение, то набор
– её оптимальное решение, то набор
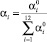 ;
; 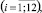 (19)
(19)
отличающийся от набора 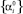 наличием дополнительного условия нормированности
наличием дополнительного условия нормированности
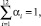 (20)
(20)
претендует считаться обоснованным набором весовых коэффициентов для линейной Z-свёртки коэффициентов набора {yi}:
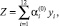 (21)
(21)
которая в соответствии с предпосылками (1)–(3) позволяет отнести анализируемое финансово-экономическое состояние исследуемого предприятия, задаваемое набором 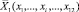 значений показателей универсального набора, к одному из перечисленных выше типов, что отвечает основной идее Z-метода Э. Альтмана.
значений показателей универсального набора, к одному из перечисленных выше типов, что отвечает основной идее Z-метода Э. Альтмана.
Тихомирова Е.И., д.э.н., профессор кафедры математических методов в экономике, декан факультета математической экономики и информатики, РЭУ им. Г.В. Плеханова, г. Москва;
Титов В.А., д.э.н., профессор кафедры информационных технологий, начальник отделения по учебной работе факультета математической экономики и информатики РЭУ им. Г.В. Плеханова, г. Москва.
Работа поступила в редакцию 18.03.2015.
[1] Показатель Z, рассчитанный по формуле (2), имеет серьёзный недостаток – его можно использовать лишь для крупных компаний, акции которых котируются на бирже (для таких компаний можно получать объективную рыночную оценку собственного капитала).
[2] Позднее Э. Альтман разработал модель оценки вероятности банкротства на горизонте пять лет [27]. В модели используются показатели: рентабельность активов, темп роста прибыли, коэффициент покрытия процентов, отношение накопленной прибыли к активам, коэффициент текущей ликвидности, коэффициент автономии, стоимость активов.
[3] Банковские аналитики предлагают использовать в числителе этого показателя стоимость внеоборотных и нематериальных активов. М. Федотова – стоимость всех активов. Е. Стоянова считает, что рыночную стоимость акций предприятия можно оценить отношением суммы дивидендов к среднему уровню ссудного процента.
Отметим, однако, что по акциям большинства российских предприятий дивиденды не выплачиваются или выплачиваются в ограниченных размерах. В связи с этим любой из перечисленных способов предполагает субъективизм в оценках и искажает результат.
[4] Так как коэффициент KКЗ/ДЗ имеет обратную направленность, то в Z-свёртке следует использовать коэффициент 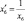 .
.
[5] Показатель x2 может принимать отрицательные значения.
[6] Для показателя x2, в случае если расчётное значение отрицательно, далее в алгоритме следует использовать значение y2 равное «0».
Библиографическая ссылка
Новикова А.Б., Халиков М.А. Z-МОДЕЛИ ОЦЕНКИ ВЕРОЯТНОСТИ БАНКРОТСТВА ПРЕДПРИЯТИЙ КОРПОРАТИВНОГО СЕКТОРА ЭКОНОМИКИ: КРИТИКА, НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ // Фундаментальные исследования. 2015. № 2-10. С. 2213-2221;URL: https://fundamental-research.ru/ru/article/view?id=37385 (дата обращения: 26.02.2026).




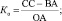
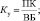
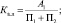
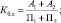
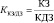 4;
4;