Параметры начальной шероховатости поверхности, которую необходимо обработать, определяются либо эксплуатационными свойствами оборудования и материалов, применяемых для предварительного шлифования, либо природными свойствами камня.
В связи с большим количеством факторов, определяющих качество поверхности и сложным характером их взаимовлияния, на данный момент не представляется возможным разработать единую модель формирования параметров шероховатости при шлифовании.
В зависимости от типа камня и его назначения рассматриваются обрабатываемые поверхности трех типов:
● поверхность камня получена с помощью предварительного грубого шлифования;
● поверхность образована распиливанием камня на отдельные плиты;
● поверхность камня образована скалыванием пластов.
Если перед шлифованием поверхность камня была подвержена грубой обработке, то шероховатость поверхности подчиняется двумерному нормальному закону распределения [1]. Аналогично поверхность камня подчиняется двумерному нормальному закону распределения в случае скалывания пластов, так как форма поверхности задается природной структурой камня.
В случае, когда поверхность образована распиливанием камня на отдельные плиты, закон распределения шероховатости по поверхности камня подчиняется двумерному равномерному закону [2].
Случайная величина Х называется нормально распределенной (имеющей распределение Гаусса), если ее плотность вероятности имеет вид
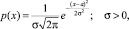
где a – средняя шероховатость; σ – среднеквадратическое отклонение значений шероховатости.
Случайная величина ХY называется двумерной нормально распределенной, если ее плотность вероятности имеет вид
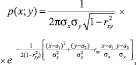(1)
где a1, a2 – средние значения шероховатостей поверхности камня в направлении осей ОХ и ОY соответственно; σx, σy – среднеквадратические отклонения шероховатостей поверхности камня в направлениях ОХ и ОY; rxy – коэффициент корреляции между шероховатостями поверхности камня в направлении осей ОХ и ОY.
Для природного камня по данным статистических исследований [3] шероховатости в направлении осей ОХ и ОY не коррелированы, тогда коэффициент корреляции rxy = 0 и функция плотности принимает вид
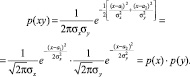(2)
Иными словами, плотность распределения шероховатостей по плоскости равна произведению плотностей шероховатостей в направлении осей ОХ и ОY, то есть случайные величины шероховатостей в направлении осей независимы между собой.
В процессе шлифования взаимодействуют абразивный круг и обрабатываемая поверхность.
Рассмотрим, какую площадь контакта имеет абразивный круг с обрабатываемой поверхностью. Пусть на поверхности абразивного круга имеется единичное зерно, которое взаимодействует с поверхностью камня (рис. 1). Их взаимодействие описывается по типу микрорезания поверхности камня, либо по типу микроскалывания [4]. При микрорезании камня абразивное зерно заглубляется в камень в среднем на величину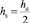 
, где ha – средняя шероховатость поверхности абразивного круга, соответственно глубина воронки в камне от резания имеет среднюю величину hз. При микроскалывании глубина воронки в камне имеет среднюю величину, существенно превосходящую hз [5].
Полагаем в среднем, что абразивное зерно имеет форму куба, который в абразивной связке расположен, как показано на рис. 1. Тогда площадь поверхности абразивного зерна – это площадь боковой поверхности пирамиды с прямыми углами при ее вершине и высотой ha, т.е. площадь трех прямоугольных треугольников. Длина стороны единичного зерна равна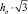 
, а площадь боковой поверхности единичного зерна, выступающего на поверхности абразивного круга, равна
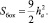(3)
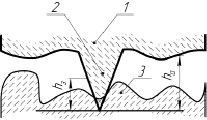
Рис. 1. Схема взаимодействия единичного зерна абразивного круга с обрабатываемой поверхностью камня: 1 – абразивный круг; 2 – единичное зерно абразивного круга; 3 – обрабатываемая поверхность камня
При этом площадь, которую единичное зерно занимает на поверхности абразивного круга, равна
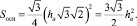(4)
Иными словами, площадь боковой поверхности пирамиды больше площади ее основания в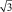 
раз. При этом фактическая площадь основания зерна с учетом той части, которая находится в связке, в два раза больше, чем площадь основания пирамиды, то есть
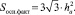(5)
Таким образом, отношение площади боковой поверхности единичного зерна, выступающего на поверхности абразивного круга, к фактической площади основания зерна будет равно
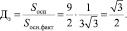(6)
Следует, однако, учесть, что объемная доля абразивных зерен в составе шлифовального круга зависит от зернистости круга и составляет порядка Дзер = 40–45 % [5]. Если объемная доля абразивных зерен, содержащихся в связке, равна Дзер, то доля рабочей площади абразивных зерен, содержащихся в связке и распределенных по поверхности шлифовального круга, с учетом (6) определяется по формуле
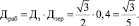(7)
В процессе шлифования доля рабочей площади абразивных зерен возрастает, так как часть камня шлифуется микроскалыванием, при этом процесс шлифования – это процесс хрупкой деформации с отрывом микрочастиц камня от основы и последующим их движением по кругу. Таким образом, часть деформированного камня продолжает участвовать в процессе шлифования, существенно увеличивая площадь контакта абразивного круга и обрабатываемой поверхности.
Следует также отметить тот факт, что процесс шлифования осуществляется на высокой скорости и срезание (скалывание) микрочастиц камня происходит многократно даже при одном прохождении шлифовальным кругом поверхности камня.
Определим долю площади, по которой происходит контакт между абразивным кругом и обрабатываемой поверхностью.
В начальный момент времени, когда шлифовальный круг касается поверхности камня, площадь контакта оказывается минимальной, поскольку обработка поверхности камня начинается при соприкосновении наиболее выступающих участков поверхности. В последующем, когда участки деформированы, шлифование происходит по большей площади соприкосновения круга и поверхности камня.
Полагая, что шероховатости поверхности камня в направлении осей ОХ и ОУ независимы, можно определить долю контакта между абразивным кругом и обрабатываемой поверхностью по оси ОХ.
Пусть в процессе одного прохождения шлифовальным кругом с поверхности камня снимается слой толщиной δ. При этом средняя шероховатость поверхности, как отмечено ранее, равна а1 (δ < а1). Задача шлифования – совершить столько проходов шлифовальным кругом, чтобы выполнялось условие
а1 < k∙δ, (8)
где k – число проходов шлифовальным кругом.
Из неравенства (8) следует, что
(9)
здесь функция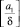 
– целая часть числа 
.
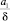На практике число проходов шлифовальным кругом k может оказаться большим, чем из формулы (9), так как в (9) k определяется по среднему размеру шероховатости, а на практике процесс шлифования ведется до тех пор, пока шероховатость камня не станет равной шероховатости абразивного круга. Так как распределение шероховатостей на поверхности камня удовлетворяет нормальному закону распределения, то с надежностью γ = 0,997 можно утверждать, что число проходов k не будет превосходить величины
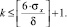(10)
Определим, какой будет доля площади, по которой происходит контакт между абразивным кругом и обрабатываемой поверхностью при первом прохождении. Так как начало прохождения поверхности происходит от точки a1 + 3σx, то после одного прохода абразивным кругом на графике будет достигнуто положение a1 + 3σx – δ (рис. 2).
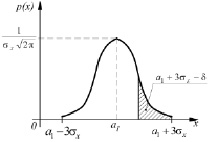
Рис. 2. Нормальное распределение шероховатостей вдоль оси ОХ и область прохождения первого участка
После финишного прохождения поверхности шлифования абразивным кругом площадь контакта между кругом и поверхностью будет полная, то есть будет равна 100 %.
Это практически соответствует площади фигуры, ограниченной кривой p(x) и осью ОХ, а также вероятности того, что значение случайной величины шероховатости после шлифования окажется меньшим a1 – 3σx. При этом вероятность того, что значение случайной величины шероховатости после шлифования окажется меньшим a1 + 3σx – δ, будет пропорциональна площади фигуры, ограниченной кривой p(x), осью ОХ и прямой x = a1 + 3σx – δ, площадь которой определяется с помощью функции Лапласа:
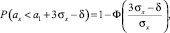(11)
где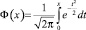 
– интегральная функция Лапласа.
Таким образом, доля площади, по которой происходит контакт между абразивным кругом и обрабатываемой поверхностью при первом прохождении поверхности будет определяться по формуле (11). Рассуждая аналогично, можно показать, что при n-м прохождении поверхности абразивным кругом доля площади контакта будет определяться по формуле
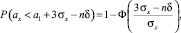(12)
при этом число n должно удовлетворять условию (10).
Нетрудно видеть, что функция (12) является монотонно возрастающей по переменной n, то есть при увеличении числа прохождений поверхности абразивным кругом доля площади контакта будет монотонно возрастать от 0 до 1.
Подводя итог рассуждениям, получим, что если шероховатость поверхности камня подчиняется двумерному нормальному закону распределения, то доля площади контакта между абразивным кругом и обрабатываемой поверхностью с учетом формул (7) и (12) определяется в виде
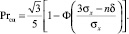(13)
Рассмотрим случай, когда распределение шероховатостей по поверхности камня подчиняется двумерному равномерному закону. Двумерное равномерное распределение задается функцией плотности:
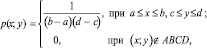
где ABCD – прямоугольник с вершинами A(a; c); B(a; d); C(b; d); D(b; c).
Будем полагать, что распределения шероховатостей в направлении осей ОХ и ОY независимы, тогда распределение шероховатостей в направлении оси ОХ подчиняется равномерному закону
Случайная величина Х называется равномерно распределенной на отрезке [a, b], если ее плотность распределения имеет вид (рис. 3)
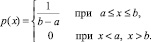(14)
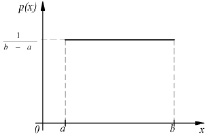
Рис. 3. График функции плотности равномерного закона распределения
Равномерное распределение шероховатостей на отрезке [a; b] означает, что на микроуровне поверхность имеет форму, показанную на рис. 1. Иными словами, на малых расстояниях равномерное распределение шероховатостей является псевдонормальным распределением [1]. В таком случае, для известных значений средних шероховатостей a1 и a2 в направлении осей ОХ и ОY соответственно и среднеквадратических отклонений шероховатостей поверхности камня в направлениях ОХ и ОУ, σx, σy применим вышеописанный алгоритм определения доли площади контакта между абразивным кругом и обрабатываемой поверхностью. При этом значения параметров a1, a2, σx, σy могут быть существенно меньшими, чем для случая двумерного нормального распределения шероховатостей, но сама доля площади контакта между абразивным кругом и обрабатываемой поверхностью может быть также определена по формуле (13).
Рецензенты:Евстратов В.А., д.т.н., профессор, зав. кафедрой «Машины и оборудование предприятий стройиндустрии», ШИ ЮРГПУ (НПИ), филиал ЮРГПУ им М.И. Платова, г. Шахты;
Кожемяченко А.В., д.т.н., профессор кафедры «Технические системы ЖКХ и сферы услуг», ИСОиП, (филиал) ДГТУ, г. Шахты.
Работа поступила в редакцию 18.03.2015.
Библиографическая ссылка
Деркачев И.С., Мицик М.Ф., Адигамов К.А., Жданова О.В., Байбара С.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФОРМИРОВАНИЯ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ КАМНЯ ПРИ ПЛОСКОМ ШЛИФОВАНИИ И ОПРЕДЕЛЕНИЕ ПЛОЩАДИ КОНТАКТА АБРАЗИВНОГО КРУГА С ПОВЕРХНОСТЬЮ // Фундаментальные исследования. – 2015. – № 2-9. – С. 1849-1853;URL: https://fundamental-research.ru/ru/article/view?id=37319 (дата обращения: 18.04.2024).