Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Cюй Юнь 1

---

1 ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет»

Рассматриваются проблемы автоматизированного проектирования соединения SHERPA в деревянных конструкциях с учётом воздействия эксцентриситета по программе Solidworks Simulation 2014. Анализируются граничные условия, физико-механические и геометрические характеристики материалов, плотность и формы автоматического построения сетки, от которых зависит несущая способность соединения. В качестве примера после создания трехмерного моделирования двух металлических накладок выполнен конечно-элементный анализ напряженно-деформированного состояния экспериментального соединения SHERPA с использованием упрощенной методики. Приводится решение задачи по определению эквивалентного напряжения, перемещения, главного напряжения и деформации соединения при воздействии на сжатие и изгиб. Показана удовлетворительная сходимость данных расчётных результатов на основе предложенных уравнений с полученными экспериментальными определениями напряженно-деформированного состояния. Подтверждена достоверность научно-исследовательской работы автора для конструкторского решения.

Статья в формате PDF

1017 KB

МКЭ

эксцентриситет

напряженно-деформированное состояние

1. Официальный сайт компании Rautaruukki. Обзор физико-механических характеров материала EN 6082 [Электронный ресурс]. – Режим доступа: http://www. ruukki.com.

2. Обзор понятий эквивалентного напряжения [Электронный ресурс]. – Режим доступа: http://en.wikipedia.org/wiki/Von_Mises_yield_criterion.

3. Обзор характеристик SHERPA и других типов соединения [Электронный ресурс]. – Режим доступа: http://artiva.lv/photo/files/sherpa_why_use_sherpa.pdf.

4. BS EN 755-2:2008. Aluminium and aluminium alloys. Extruded rod/bar, tube and profiles. Mechanical properties.

5. SolidWorks 2014 Tutorial with Video Instruction, 2014. [Электронный ресурс]. – Режим доступа: http://www.sdcpublications.com/pdfsample/978-1-58503-855-8-1.pdf.

В диссертационной работе автора были проведены численные и экспериментальные исследования несущей способности соединения SHERPA [3] без укрепления и с МЗП (Металлические Зубчатые Пластины) при изгибе в деревянных конструкциях из комбинации стеновой панели-CLT с балкой-CLT и LVL. С целью проверки достоверности расчётных результатов используется метод конечных элементов (МКЭ). С применением программы Solidworks Simulation 2014 [5] после выполнения трехмерного моделирования двух металлических накладок и численного расчёта будут вычислены эквивалентное напряжение, перемещение, главное напряжение и деформация.

Целью настоящей работы является определение напряженно-деформированного состояния на опытных металлических накладках по программе Solidworks Simulation 2014, проверка достоверности экспериментального и численного исследования определения несущей способности соединения SHERPA при изгибе в деревянных конструкциях.

При проектировании соединения SHERPA особое внимание уделяется контактным зонам между выступами двух металлических накладок, на которых воспринимают значительные усилия, обусловливающие пластическое разрушение. По существу, для выяснения распределения локального напряжения несущей способности крепежа SHERPA, часть из которого отдельно крепится к торцовой поверхности стеновой панели-СLT и балки из CLT и LVL, была разделена на два типа по определению несущей способности крепежа SHERPA при изгибе:

● при приложении нагрузки вдоль направления вставки без учёта эксцентриситета, Н;

● при приложении нагрузки вдоль направления вставки с учётом эксцентриситета, Н;

Таблица 1

Физико-механические характеристики панели-CLT

Исследование физико-механических характеристик для панели-СLT на основе результатов в соответствии с руководствами по различным компаниям представлено в табл. 1.

Из табл. 1 видно, что модуль упругости для панели-CLT выше, чем LVL, в соответствии с СНиП 64. 13330.2011, и полученная плотность для панели-CLT соответствует с известным нормативным значением.

После выполнения трехмерной модели соединения SHERPA для каждого элемента назначали физические и механические характеристики материалов в соответствии с EN AW 6082 [1]:

● модуль упругости E = 70000 МПа;

● коэффициент Пуассона μ = 0,33;

● модуль жесткости G = 26400 МПа;

● плотность ρ = 2,7 г/см3 [3];

● для куба алюминий с толщиной от 5 до 25 мм:

напряжение текучести минимально до 260 МПа;

напряжение на растяжение минимально до 310 МПа.

Для того чтобы повысить точность модели, при расчёте несущей способности соединения при изгибе используется упрощенная методика: деревянными элементами из стеновой панели-CLT с балкой из CLT и LVL можно пренебречь; с учётом типа крепления шурупов в гнездах металлических накладок должно осуществиться зафиксированным креплением; на контрактном зоне между выступами двух металлических накладок при сжатии 319,48 МПа; в гнездах отверстий шурупов воспринимается изгибающий момент (при приложении эквивалентного действующего усилия 44800 Н) на верхних и нижних гнездах.

Построение сетки автоматично выполняется по компьютеру. Расположение мест приложения нагрузки и крепления для соединения SHERPA представлено на рис. 1, а.1–а.2.

Рис. 1. Расположение мест приложения нагрузки и крепления для металлической накладки: а.1–а.2 – без учёта эксцентриситета; б.1–б.2 – с учётом эксцентриситета

Экспериментальные исследования по МКЭ с помощью программы Solidworks Simulation 2014 были направлены на определение:

● напряжения von Mises (эквивалентное напряжение по фон Мизесу исходя из соответствующей гипотезы прочности или критерия пластичности) [2], МПа;

● максимальной деформации на металлической накладке по пределу текучести материала, мм;

● главного напряжения, МПа, и деформации, 10–6 мм/мм;

● максимального перемещения, мм.

По программе SolidWorks Simulation 2014 выполняется расчёт несущей способности крепежа SHERPA под нагрузкой вдоль направления вставки без учёта эксцентриситета. Сравнения расчётных и экспериментальных результатов определения деформации и напряжения на металлической накладке, которая крепится к стеновой панели-CLT и балке из CLT и LVL при приложении различных нагрузок без и с учётом эксцентриситета, представлены в табл. 2 и 3.

На рис. 2 показаны расчётные виды пластического разрушения металлических накладок под нагрузкой вдоль направления вставки без учёта эксцентриситета с использованием программы Solidworks Simulation 2014, а экспериментальные представлены на рис. 3.

Из табл. 1 и 2 видно, что на контактных участках между выступами двух металлических накладок при сжатии и растяжении появилась отчётливая концентрация напряжения. При приложении нагрузки до 15000 Н максимальное напряжение 533,3 МПа выше в 105 раз, чем предел текучести материала 260 МПа. На рис. 2 и 3 видно, что без учёта эксцентриситета на контактной зоне возникает отчётливое перемещение и одновременно на гнездах отверстий шурупов относительно небольшая деформация. По сравнению двух результатов можно сделать вывод о том, что расчётные результаты по МКЭ могут относительно полностью отражать и объяснить причину пластического разрушения металлических накладок.

Таблица 2

Сравнение расчётных и экспериментальных результатов определения деформации и напряжения на металлической накладке, которая крепится к стеновой панели-CLT без учёта эксцентриситета

Таблица 3

Сравнение расчётных и экспериментальных результатов определения деформации и напряжения на металлической накладке, которая крепится к балке из CLT и LVL без учёта эксцентриситета

а.1 а.2

а.3 а.4

б.1 б.2

б.3 б.4

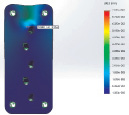
Рис. 2. Виды разрушения металлических накладок при изгибе без учёта эксцентриситета: а.1–а.2 – распределение эквивалентных напряжений на лицевой и оборотной сторонах металлических накладок в стеновой панели-CLT; а.3–а.4 – изменение перемещений то же в стеновой панели-CLT; б.1–б.2 – распределение эквивалентных напряжений то же в балке из CLT и LVL; б.3–б.4 – изменение перемещений то же в балке из CLT и LVL

Поскольку в узловом соединении может возникнуть изгибающий момент, обусловливающий пластичное разрушение металлических накладок, экспериментальные исследования проведены с учётом эксцентриситета на металлические накладки по МКЭ. На рис. 1, б.1–б.2 показано расположение мест приложения нагрузки и крепления соединения SHERPA. Расчётные виды разрушения металлических накладок при изгибе с учётом эксцентриситета по программе Solidworks Simulation 2014 представлены на рис. 4, а экспериментальные представлены на рис. 3, б.1–б.2.

а.1 а.2 б.1 б.2

Рис. 3. Виды разрушения металлических накладок при изгибе: а – без учёта эксцентриситета; б – с учётом эксцентриситета

На рис. 5 и 3, б.1–б.2 видно, что с учётом эксцентриситета на контрактной зоне между выступами двух металлических накладок и в гнездах отверстия шурупов при изгибе появилось отчётливое перемещение. По сравнению с рис. 2 и 3 видно, что эксцентриситет может приводить к большим пластическим разрушениям металлических накладок. Если при конструировании не рассчитается влияние эксцентриситета на несущую способность соединения при изгибе, расчётные результаты будет превышать фактические. Поэтому при расчёте несущей способности соединения деревянных конструкций на металлических накладках SHERPA при изгибе должен учитываться коэффициент эксцентриситета.

Для проверки работоспособности предложенных методик дополнительно были приложены одинаковые нагрузки на металлические накладки. Сравнения расчётных и экспериментальных результатов определения главного напряжения и деформации с учётом эксцентриситета представлены в табл. 4 и 5 в соответствии с графиком на рис. 6.

Из табл. 4 и 5 видно, что при расчёте по МКЭ получена удовлетворительная сходимость результатов, минимальное расхождение опытных результатов и численных. После сравнительного анализа можно сделать вывод о том, что с использованием метода конечных элементов и программы Solidworks Simulation 2014 можно выражать и определить напряженно-деформированное состояние металлических накладок. Следовательно, при конструировании могут осуществляться оценка несущей способности и совершенствование проектирования соединения SHERPA.

Таблица 4

Сравнение расчётных и экспериментальных результатов определения главного напряжения

Таблица 5

Сравнение расчётных и экспериментальных результатов определения главной деформации

а.1 а.2

а.3 а.4

б.1 б.2

б.3 б.4

Рис. 4. Виды разрушения металлических накладок при изгибе с учётом эксцентриситета: а,1–2 – распределение эквивалентных напряжений на лицевой и оборотной сторонах металлических накладок в стеновой панели-CLT; а,3–4 – изменение перемещений то же в стеновой панели-CLT; б,1–2 – распределение эквивалентных напряжений то же в балке из CLT и LVL; б,3–4 – изменение перемещений то же в балке из CLT и LVL

Вывод

1. Рассматриваются проблемы автоматизированного проектирования соединения SHERPA при изгибе с учётом эксцентриситета по программе Solidworks Simulation 2014.

2. Определено эквивалентное напряжение, перемещение, главное напряжение и деформация соединения при воздействии на сжатие и изгиб.

3. Показана удовлетворительная сходимость данных расчётных результатов на основе предложенных уравнений с полученными экспериментальными для определения напряженно-деформированного состояния, подтверждена достоверность научно-исследовательской работы автора для конструкторского решения.

Глухих В.Н., д.т.н., профессор, заведующий кафедрой технической механики, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург;

Черных А.Г., д.т.н., профессор, ректор СПГХПА, г. Санкт-Петербург.

Работа поступила в редакцию 10.03.2015.

Библиографическая ссылка