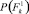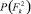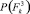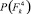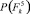Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Соколов В.А. 1

---

1 ФГАОУ ВО «Санкт-Петербургский государственный политехнический университет»

Для решения задач по определению достоверной картины технического состояния здания и его конструктивных элементов предлагается подход, основанный на вероятностном теоретическом аппарате статистических методов технической диагностики. В статье приведен пример диагностирования состояний участков бутовых фундаментов для зданий старой городской застройки на основе уровневой формулировки задачи. Для построения иерархической схемы использованы методы теории информации, основанные на таких понятиях, как информационная энтропия, максимальная энтропия, остаточная энтропия (степень определенности или количество внесенной информации), а также вероятность степени определенности. Сформулировано решающее правило диагностирования, которое состоит в том, что объект с комплексом диагностических признаков К* относится к состоянию Si, если апостериорная вероятность этого состояния является наибольшей. На основе уровневого анализа получены численные значения вероятностей отнесения фундаментов здания к установленным в нормах пяти категориям технического состояния.

Статья в формате PDF

1019 KB

техническая диагностика

вероятностные методы диагностирования

формула Байеса

методы теории информации

энтропия

максимальная энтропия

остаточная энтропия

уровневая формулировка задачи

иерархическая схема диагностирования фундаментов

1. Биргер И.А. Техническая диагностика. – М.: Изд-во «Машиностроение», 1978. – 240 с.

2. Соколов В.А. Вероятностный анализ технического состояния (ВАТС) элементов строительных систем // Дефекты зданий и сооружений. Усиление строительных конструкций: сборник трудов XIV научно-методической конференции. – СПб.: ВИТУ, 2010. – С. 41–49.

3. Соколов В.А. О пороговом значении при определении вероятностей состояний строительных конструкций // Вестник гражданских инженеров. – СПбГАСУ, 2013. – № 4. – С. 67–73.

4. Соколов В.А. Определение технического состояния строительных конструкций зданий на основе многоуровневого вероятностного анализа // Научный электронный журнал «Предотвращение аварий зданий и сооружений». – М., 2012.

5. Соколов, В.А. Оценка технического состояния элементов строительных систем с использованием вероятностных методов распознавания // Наука и безопасность. – 2011. – № 1.

6. Соколов В.А. Оценка технического состояния строительных конструкций зданий на основе многоуровневого вероятностного анализа // Инженерно-строительный журнал. – СПбГПУ, 2011. – № 7. – С. 45–51.

7. СП 13-102-2003. Правила обследования несущих строительных конструкций зданий и сооружений. Свод правил по проектированию и строительству. – М.: Госстрой России. ГУЛ ЦПП, 2003. – 28 с.

8. Файнстейн А. Основы теории информации. – М.: Изд-во иностранной литературы, 1960. – 240 с.

9. Шеннон К. Работы по теории информации и кибернетики. – М.: Изд-во иностранной литературы, 1963. – 504 с.

10. Sokolov V.A. Probabilistic Analysis of Intermediate Floor Steel and Wooden Structures in the Old Urban Development Building (2014) Applied Mechanics and Materials, vol. 633–634, Р. 1040–1048.

Постановка задачи при вероятностных методах распознавания такова. Имеется система (конструктивный элемент, здание или сооружение в целом), которая находится в одном из случайных состояний Si. Считается, что состояния сформулированы в соответствии с пятью категориями в нормах [7]. Предполагается также, что сформулирована совокупность признаков, каждый из которых с определенной вероятностью характеризует состояние системы (конструкции). В итоге требуется построить решающее правило, с помощью которого предъявленная (диагностируемая) совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов).

Важное место в решении задач распознавания состояний систем отводится статистическим методам. Главное их преимущество состоит в возможности одновременного учета диагностических признаков различной физической природы, так как они характеризуются безразмерными величинами – вероятностями их проявления при различных состояниях системы. Одним из основных статистических методов является метод, основанный на байесовском подходе [1].

В расчетах удобно пользоваться обобщенной формулой Байеса, которая может быть записана так:

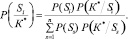(1)

Для определения вероятности состояний по методу Байеса составляется диагностическая матрица. Это таблица, которая строится на основе предварительного статистического материала, т.е. в нее включены априорные вероятности состояний и признаков (табл. 1). Как видно, приняты пять состояний Si (исправное, работоспособное, ограниченно работоспособное, недопустимое и аварийное) и шесть двухразрядных диагностических признаков kjs. После проведения серии расчетов на основе байесовской процедуры по зависимости (1) получается распределение апостериорных вероятностей P(Si/K*) диагностируемых состояний. Решающее правило, в соответствии с которым принимается решение о конкретном диагнозе, состоит в том, что объект с комплексом признаков К* относится к состоянию Si, если апостериорная вероятность этого состояния Si является наибольшей, т.е.

К* ∈ Si,

если P(Si/К*) > P(Sj/К*)

(j = 1, 2, …, n; i ≠ j). (2)

Предложенная процедура диагностирования с использованием методов распознавания состояний и методов теории информации для строительных конструкций зданий применена впервые, что определяет научную новизну работы.

Основная часть

Сказанное выше иллюстрируется примером диагностики состояний участков фундаментов здания старой городской постройки, имеющего прямоугольную планировочную компоновку. Схематично здание представлено на рис. 1.

Ленточный бутовый фундамент здания разделяется на четыре участка, т.е. по количеству стен – участок фундамента лицевой стены F1, участок фундамента дворовой стены F2, и участки фундаментов торцевых стен F3 и F4. После обследования каждого участка выявляется наличие или отсутствие указанных в табл. 1 разрядов признаков диагностирования kjs, или, как это принято в технической диагностике, выявляется реализация признаков 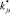. Обследование фундаментной части зданий осуществляется, как известно, по результатам проходки необходимого количества пристенных шурфов.

Пусть, например, для первого участка фундамента F1 лицевого фасада при обследовании очередного здания реализация вероятностей признаков p(kis/Si) получилась в виде следующей последовательности: первый признак реализовался в виде k12, второй признак – k22, третий признак – k32, четвертый признак – k42, пятый признак – k51, шестой признак – k62. Численные значения вероятностей p(kis/Si) в соответствующих строках матрицы выделены цветом (табл. 1). После этого для рассматриваемого участка фундамента выполняется расчет апостериорных вероятностей P(Si/K*) по обобщенной формуле Байеса (1). В результате распределение апостериорных вероятностей в соответствующих обозначениях для F1 получилось в виде следующего ряда чисел:

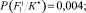
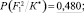
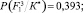
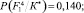
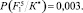
Как видно, участок фундамента лицевой стены F1 в данном примере в соответствии с правилом (2) может быть отнесен ко второй категории технического состояния с вероятностью 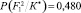. Учитывая выведенное в работе [3] пороговое значение вероятностей состояний Pl = 0,690 для суммы первых трех вероятностей, эксперт такое решение может принять с полной уверенностью. Следует отметить, что байесовскую процедуру диагностирования состояний проходят только элементы системы низшего (базисного) уровня. В данном примере – это указанные участки фундаментов стен, по результатам диагностирования и обработки вероятностных параметров которых строится дальнейшая процедура определения категории технического состояния для подсистемы следующего уровня – фундаменты F в целом. Для этого анализ полученных выше численных значений 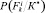осуществляется с использованием методов теории информации [1, 8, 9].

Центральное место в теории информации занимает понятие энтропии системы. Энтропия в теории информации характеризует степень неопределенности системы. Как известно, энтропия системы с одинаковыми вероятностями состояний равна логарифму числа состояний [1–6, 10].

В данном случае при n = 5 значение H(S)max = log 5 ≈ 0,700. С учетом априорных вероятностей состояний P(Si) из табл. 1 (выделены шрифтом и цветом) максимальное значение равно H(S)max = 0,598. Чем ближе энтропия элемента системы к этому значению, тем больше неопределенность при распознавании его состояний. Чем она дальше, т.е. ближе к нулю, тем неопределенность ниже, а значит выше определенность.

Рис. 1. Общий вид здания. Схема

Таблица 1

Диагностическая матрица для участков фундаментов

В рассматриваемом примере в обозначениях для элемента F1 энтропия H(F1) состояний этого элемента получилась равной 0,451. Для продолжения дальнейшего анализа вводится понятие степени определенности рассматриваемого элемента системы в соответствии с зависимостью

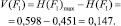
Таким образом, обследуемый элемент – «участок фундамента F1» с вероятностью 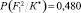относится ко второй (работоспособной) категории технического состояния со степенью определенности этого состояния, равной V(F1) = 0,147. Эти параметры в дальнейшем используются при анализе технического состояния и степени его определенности уже для более сложной структуры – фундамента в целом (подсистемы здания).

Пусть далее, для второго F2, третьего F3 и четвертого F4 участков фундаментов этого здания при той же диагностической матрице (табл. 1), но при других реализациях признаков 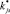, распределение расчетных апостериорных вероятностей 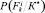получилось, например, следующим (формула (1)).

− Для F2

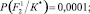
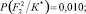
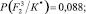
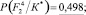
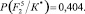
Энтропия

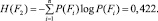
Максимальная энтропия с учетом априорных вероятностей состояний P(Si) также равна H(F2)max = 0,598.

Степень определенности (остаточная энтропия или количество внесенной информации)

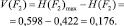
− Для F3

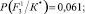
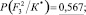
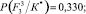
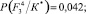
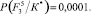
Энтропия

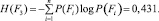
Степень определенности

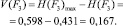
− Для F4

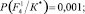
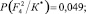
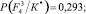
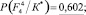
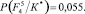
Энтропия

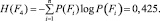
Степень определенности

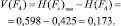
Полученные вероятностные параметры удобно свести в табл. 2. На основании данных этой таблицы далее рассматривается пример построения решения для диагностирования состояний подсистемы следующего уровня – «фундамент F» по совокупности состояний его участков.

В статьях [2, 4, 10] показано, что при определенных допущениях (независимость состояний как случайных событий, но, в то же время их совместность) энтропия состояния подсистемы равна сумме энтропий состояний составляющих ее элементов, то есть для совокупности «фундаменты F = F1 F2 F3 F4» принято

H(F) = H(F1) + H(F2) + H(F3) + H(F4) = 1,730.

Там же, в [2, 4, 10], доказано, что это справедливо и для остаточной энтропии (степени определенности), а именно

V(F) = V(F1) + V(F2) + V(F3) + V(F4) = 0,662.

Дальнейшее построение решения возможно только в вероятностном виде, поэтому вводится понятие вероятностей степени определенности P(Vk), которые определяются по следующим зависимостям:

P(V1) = V(F1)/V(F) = 0,222;

P(V2) = V(F2)/V(F) = 0,265;

P(V3) = V(F3)/V(F) = 0,252;

P(V4) = V(F4)/V(F) = 0,261.

Именно эти значения занесены в 9-й столбец табл. 2. В таблице индекс k означает номер участка фундамента (k = 1, 2, 3, 4). Очевидно, что ∑ P(Vk) = 1,0.

Таблица 2

Результаты вероятностного расчета для подсистемы «фундамент F»

Вероятности степени определенности P(Vk) определяют вклад (долю) состояния каждого элемента в состояние подсистемы следующего уровня. Для перехода с уровня базисных элементов, в данном случае участков фундамента, на следующий уровень диагностирования, представляющий собой подсистему «фундамент F = F1 F2 F3 F4», автором предложены зависимости, позволяющие получить распределение вероятностей состояний для этой подсистемы. Зависимости имеют следующий вид:

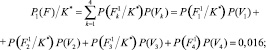
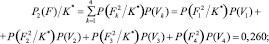
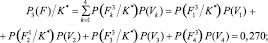
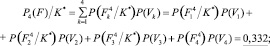
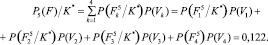(3)

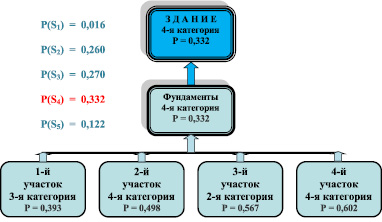
Рис. 2. Часть общего «диагностического дерева» здания (ветвь) для подсистемы «фундаменты»

Таким образом, следуя правилу (2), техническое состояние фундаментов здания можно отнести к четвертой категории с вероятностью P4(F)/K* = 0,332. С учетом выведенного в работе [3] порогового значения для вероятностей состояний такое решение и на этом уровне диагностирования можно принять с полной уверенностью.

Графической моделью предложенной процедуры является так называемое «диагностическое дерево», пример построения которого для всех конструктивных подсистем всего здания – фундаменты, стены, перекрытия и крыша, со своей иерархией подструктур и уровнями разделения, представлен в статьях [4, 6, 10]. В данном случае рассмотрена только часть этого «дерева» – ветвь, отражающая уровневую иерархию для фундаментов здания. Эта ветвь схематично в виде диаграммы проиллюстрирована на рис. 2. Как видно, ветвь представлена трехуровневой иерархической моделью.

Выводы

Разработана методика диагностирования фундаментов здания с использованием статистических методов распознавания состояний технической диагностики, основанных на байесовской процедуре. Для диагностирования состояний фундаментов здания построена графическая модель, как часть (ветвь) общего «диагностического дерева» здания в целом. Ветвь представлена трехуровневой иерархической структурой (рис. 2). Для прохождения по уровням этой структуры предложен алгоритм, основанный на методах теории информации. Для этого сформулировано понятие «информационный вклад (или доля)» на основе использования методов теории информации с применением понятия информационной энтропии. Приведен пример диагностирования состояний фундаментов здания, по результатам которого подсистему «фундаменты здания» можно отнести к четвертой категории технического состояния с вероятностью P4(F)/K* = 0,332. Следует отметить, что этот результат можно применить и к зданию в целом, если, допустим, требуется оценить его состояние только по состоянию фундаментов.

Барабанщиков Ю.Г., д.т.н., профессор кафедры «Строительство уникальных зданий и сооружений», ФГАОУ ВО «СПбПУ», г. Санкт-Петербург;

Никольский С.Г., д.т.н., профессор кафедры «Строительство уникальных зданий и сооружений», ФГАОУ ВО «СПбПУ», г. Санкт-Петербург.

Работа поступила в редакцию 10.03.2015.

Библиографическая ссылка