В метровом и декаметровом диапазонах при наличии нормальных помех оптимальная обработка сигналов сводится к построению различных корреляционных приемников. Однако в этих диапазонах волн достаточно часто имеют место импульсные, а точнее квазиимпульсные помехи с доминирующим воздействием импульсной составляющей.
Достоверность навигационной информации, передаваемой с помощью авиационной системы связи, и достоверность навигационных поправок, передаваемых спутниковыми радионавигационными системами, – одно из узловых требований для успешного функционирования систем УВД при АЗН.
В этой связи возникает задача оценки эффективности методов помехоустойчивого кодирования, подверженных квазиимпульсным помехам при традиционно используемом корреляционном методе оптимального приема.
Для радиосвязных каналов, подверженных нормальным помехам, чаще всего используются два типа помехоустойчивых кодов – блочный код и сверточный код. Рассмотрим возможности применения этих кодов при наличии квазиимпульсных помех.
Как известно, при цифровой передаче данных выходное отношение сигнал/(шум + помеха), рассчитывается как
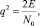(1)
где Е и N0 – соответственно, энергия сигнала, передающего бит информации, и спектральная плотность помех.
Важно подчеркнуть, что в канале передачи информации соседствуют разнообразные помехи – флуктуационные, квазиимпульсные, собственные шумы приемника и некоторые другие. Это с необходимостью требует использовать коды, имеющие большие кодовые расстояния, т.е. такие, которые могут корректировать возникающие ошибки. Анализ показывает, что с такой задачей коды с большими кодовыми скоростями оказываются непригодными. В этой связи ограничивалась длина кодов, используемых для моделирования n ≤ 100, и кодовая скорость кодов R = 0,4 – 0,6.
Кодирование осуществлялось по стандартной схеме на основе регистра сдвига длиной п – k, где k = п R – число информационных символов кода, с обратными связями, структура которых задается порождающим многочленом
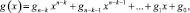(2)
где gi (i = 0, n – k) – коэффициенты порождающего многочлена, определяющие наличие либо отсутствие обратной связи в i-й ячейке.
Рис. 1 иллюстрирует зависимости вероятности ошибки на 1 бит информации Pe от отношения сигнал/шум при приёме сигналов ФМ-2 коррелятором (приёмником) для случаев использования различных методов блочного кодирования и декодирования при значении параметра импульсности Vd, равном значению 5 дБ, что характерно для промежуточной помехи при значении полосы приемника В = 4,8 кГц, типичном при передаче данных в метровом диапазоне со скоростью 4800 бит/с.
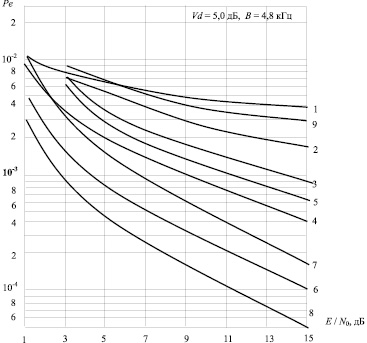
Рис. 1. Помехоустойчивость корреляционного приема ФМ сигналов с использованием блочных кодов при действии индустриальных помех: 1 – ФМ без кодирования; 2 – код (7, 4, 3); 3 – код (15, 7, 5); 4 – код (23, 12, 7); 5 – код (21, 11, 6); 6 – код (47, 24, 11); 7 – код (73, 45, 10) без перемежения; 8 – код (73, 45, 10); 9 – код (23, 12, 10) без перемежения
Как следует из рассмотрения рис. 1, влияние отношения сигнал/шум при наличии квазиимпульсных помех на помехоустойчивость проявляется слабо в ситуациях, когда прием сигнала осуществляется коррелятором. Принципиальное отличие сверточных кодов от блочных кодов заключается в том, что для них отсутствуют соответствующие алгебраические методы, позволяющие давать оценку на целесообразность их использования. При оценке эффективности использования сверточных кодов принимается скорость кодирования, равная R = 0,5.
При выборе наилучших сверточных кодов использованы рекомендации работы [5]. Как показано в [4], почти у всех этих кодов свободное расстояние достигает верхней границы, что свидетельствует об их оптимальности. На рис. 2 приведены кривые помехоустойчивости приема сигналов ФМ-2 в условиях действия индустриальных помех при использовании рекомендованных в [5] кодов, декодируемых по алгоритму Витерби.
Рис. 2 достаточно наглядно и убедительно свидетельствует, что с увеличением длины кодового ограничения имеет место существенное увеличение помехоустойчивости. При этом, как видно, целесообразнее использовать более сложный код, чем идти по пути роста энергии сигнала.
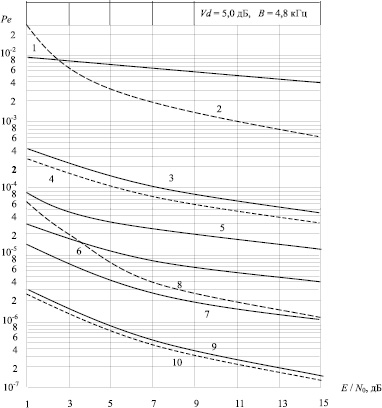
Рис. 2. Помехоустойчивость корреляционного приема ФМ сигналов с использованием сверточных кодов при действии индустриальных помех: 1 – ФМ без кодирования; 2, 3, 4 – код (7, 5); 5 – код (17, 15); 6 – код (35, 3); 7 – код (73, 61); 8, 9, 10 – код (171, 133); 
канал с перемежением данных; 
канал без перемежения данных; 
канал с независимыми ошибками
При увеличении длины кода перемежение данных даёт относительно меньший эффект с точки зрения повышения помехоустойчивости.
Если проводить оценку эффективности применения блочных и сверточных кодов в канале с квазиимпульсными помехами при использовании линейного корреляционного приёма, то можно увидеть, что при применении алгоритмов, примерно равной сложности и одинаковых скоростях кодирования, близких по значению к 0,5, целесообразнее воспользоваться сверточными кодами, декодируемыми по алгоритму Витерби, поскольку он обеспечивает наилучшие характеристики энергетической эффективности.
Уровень помехоустойчивости, который можно достичь в канале передачи данных метрового диапазона радиоволн при наличии промышленных помех при использовании свёрточного кодирования и перемежения данных, дает возможность выйти на уровень вероятности ошибки порядка 10–7 при вероятности ошибки на выходе демодулятора, равной 4∙10–3 и идеальной фазовой синхронизациях.
Эффективность систем передачи данных по каналам связи с квазиимпульсными помехами во многом зависит от адекватности приемника типу помех. В [1, 2] показано, что асимптотически оптимальный приемник для обнаружения и оценки параметров слабого сигнала в условиях действия негауссовых помех состоит из нелинейного элемента с характеристикой, определяемой распределением помехи, и линейного приемника корреляционного типа, оптимального при гауссовой помехе.
В [6] показано, что при квазиимпульсных помехах типа индустриальных и атмосферных замена оптимального нелинейного элемента на двусторонний линейный ограничитель с фиксированным порогом на уровне среднеквадратического значения огибающей фоновой составляющей помехи не приводит к существенному проигрышу в отношении сигнал/шум. При этом даже при нулевом пороге проигрыш оказывается небольшим, снижающимся с ростом значения параметра импульсности помехи Vd и не превышает 2 дБ.
Исходя из изложенного, при анализе эффективности помехоустойчивого кодирования в цифровых каналах связи в сочетании с оптимизацией обработки сигнала в условиях действия квазиимпульсных помех моделирование целесообразно проводить применительно к приемнику, включающему в себя входной фильтр с эффективной полосой пропускания В, предельный ограничитель и линейный приемник, причем моделирование целесообразно проводить применительно к сигналу ФМ-2 как наиболее помехоустойчивому.
Известно [5], что эффективность рассматриваемого квазиоптимального приемника возрастает с ростом ширины полосы входного фильтра (ΔF) и, соответственно, с ростом числа некоррелированных отсчетов n на длительности одного такта. Тем не менее, ΔF должна быть меньше частотного интервала между рядом находящимися каналами радиосвязи. В соответствии с существующими нормами, установленными для гражданской авиации для метрового диапазона частот регламентировано ΔF = 25 кГц. Такой показатель установлен для следующих значений параметров: R = 4800 бит/с и V = 1000 км/ч (путевая скорость).
Требование некоррелированности отсчетов выводит на соотношение
n = Вт = В/Вs, (3)
где Вs – ширина спектра сигнала; т – длительность посылки.
Значения параметра n превосходят число 4. Однако в декаметровом диапазоне межканальный частотный разброс меньше, чем в метровом диапазоне, для этого случая принималось n = 2.
Рис. 3 иллюстрирует результаты моделирования канала передачи без какого-либо кодирования для двух значений полосы пропускания входного фильтра при квазиоптимальном приёме.
Как видно, помехоустойчивость жёстко следит за полосой пропускания, возрастая при её увеличении и убывая при её уменьшении. Этот эффект более заметен в случаях воздействия квазиимпульсных помех по сравнению со случаем нормальной помехи.
При увеличении параметра импульсности Vd этот эффект становится более заметным.
Из сравнения приведённых кривых, характеризующих помехоустойчивость при воздействии атмосферных и промышленных помех, вероятность ошибки (на бит информации) – Pe, возникающая при атмосферных помехах, существенно ниже.
Обратим внимание, что корреляционная обработка приводит к противоположной картине.
В общем случае проводимая в условиях воздействия квазиимпульсных помех оптимизация влечёт за собой существенное уменьшение вероятности ошибок на выходе демодулятора по сравнению с ситуацией линейной обработки.
В этой ситуации повышение помехоустойчивости приёма лежит на путях применения помехоустойчивого кодирования.
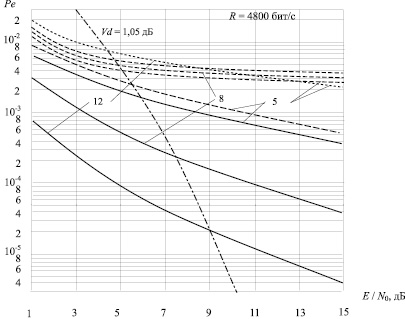
Рис. 3. Помехоустойчивость квазиоптимального приема ФМ сигналов при действии гауссовой и квазиимпульсных помех: 
гауссовская помеха; 
атмосферная помеха, В = 4,8 кГц; 
индустриальная помеха, В = 9,6 кГц; 
индустриальная помеха, В = 4,8 кГц; 
атмосферная помеха, В = 9,6 кГц
Проведём оценку эффективности использования для этого блочных кодов. Из выполненного анализа вытекает, что наибольшее значение параметра импульсности помех характерно для декаметрового диапазона волн. Из этого вытекает необходимость детального анализа квазиоптимального алгоритма приёма сигнала ФМ-2 в этом диапазоне.
На рис. 4 представлены совокупности кривых, характеризующих помехоустойчивость, для случая отсутствия кодирования (кривая 1) и для случая использования блочных кодов, у которых (Vd = 8 дБ, B = 9,6 кГц, R = 4800 бит/с, n = 2) (кривая 2).
Итак, даже коротких кодов типа (15, 7, 5), (23, 12, 7), (21, 11, 6) и при параметре сигнал/шум < 15 дБ значение вероятности ошибки составляет величину Pe = 10–5.
Ещё одно отличие, имеющее место в случае применения помехоустойчивого кодирования вместо линейного приёма, состоит в существенно меньшей эффективности перемежения для длинных кодов (кривые 7 и 8). Однако, когда применяются короткие коды, использование перемежения весьма перспективно, поскольку отказ от него приводит к тому, что граничное значение параметра сигнал/шум, обеспечивающего положительный эффект на уровне (Pe = 10–5), вследствие использования кодирования заметно возрастает.
В качестве примера могут служить следующие числовые показатели. Использование кода (7, 4, 3) даёт возможность увеличить порог на 4,5 дБ. Таким образом, влияние на помехоустойчивость закона и глубины перемежения при использовании режима квазиоптимального приёма по сравнению с линейным приёмом существенно ниже.
Кривые, представленные на рис. 5, иллюстрируют помехоустойчивость в каналах радиосвязи, подверженных атмосферным помехам, для случая применения свёрточного кодирования.
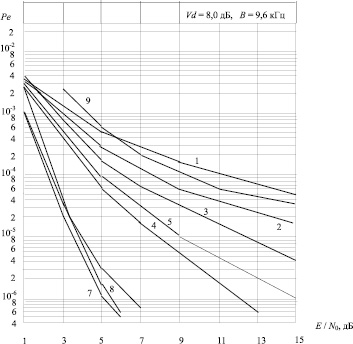
Рис. 4. Помехоустойчивость квазиоптимального приема ФМ сигналов с использованием блочных кодов при действии атмосферных помех: 1 – ФМ без кодирования; 2 – код (7, 4, 3); 3 – код (15, 7, 5); 4 – код (23, 12, 7); 5 – код (21, 11, 6); 6 – код (47, 24, 12); 7 – код (73, 45, 10); 8 – код (73, 45, 10) без перемежения; 9 – код (7, 4, 3) без перемежения
Как видно из рис. 5, использование при Vd = 5 дБ простейшего кода (7, 5), у которого ν = 2, который при декодировании по Витерби корректирует практически все одноразовые ошибки и даёт возможность получить на выходе декодера Pe = 10–5 при значении параметра сигнал/шум = 4,5 дБ.
Применение кодирования увеличивает значение параметра сигнал/шум на 34 дБ. Расчёты показывают, что при Vd = 8 дБ выигрыш оказывается ещё более заметным.
Полученные характеристики помехоустойчивости и аналогичные характеристики для режима линейного приёма показывают, что для получения допустимых значений вероятности ошибок на выходе декодера можно применять короткие помехоустойчивые коды.
При средних величинах параметра сигнал/шум на уровне от 13 до 15 дБ и применении кодов, у которых ν > 2, можно добиться уровня вероятности ошибок на выходе декодера вплоть до 10–7 и даже ниже. Обратим внимание, что использование кода (171, 133) даёт возможность достичь такой же вероятности даже при значении параметра сигнал/шум на уровне 3 дБ.
Как видно, имеет место для свёрточного и блочного кодирований типа зависимостей помехоустойчивости цифрового демодулятора с ситуацией, когда кодирование не производится. Важно отметить, что на помехоустойчивости рост отношения сигнал/шум практически не оказывает.
Кривые рис. 3 и 4 дают возможность увидеть, что при средних величинах для параметра сигнал/шум и Vd = 8 дБ вполне допустимый уровень помехоустойчивости – Pe = 10–5 в режиме квазиоптимального приёма можно реализовывать без специального помехоустойчивого кодирования, надобность в котором требуется при небольшой величине параметра Vd, относящегося к атмосферной помехе.
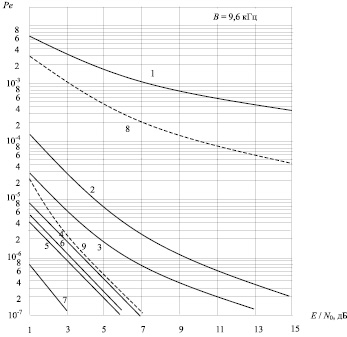
Рис. 5. Помехоустойчивость квазиоптимального приема ФМ сигналов с использованием сверточных кодов при действии индустриальных помех: 1, 8 – ФМ без кодирования; 2, 9 – код (7, 5); 3 – код (17, 15); 4 – код (35, 23); 5 – код (73, 61); 6 – код (75, 33); 7 – код (171, 133); 
Vd = 5 дБ, 
Vd = 8 дБ
Таким образом, недооценка несовпадения распределения промышленных и атмосферных помех с гауссовым, особенно на этапах, когда осуществляется проектирование и непосредственно проводятся испытания радиоэлектронной аппаратуры, эксплуатируемой в метровом и декаметровом диапазонах, сказывается на заметном ухудшении качества её функционирования.
Рецензенты:
Козлов А.И., д.ф.-м.н., профессор кафедры «Техническая эксплуатация радиоэлектронного оборудования воздушного транспорта», Московский государственный технический университет гражданской авиации, г. Москва;
Акиншин Р.Н., д.т.н., доцент, ведущий научный сотрудник секции по оборонным проблемам Министерства обороны (при Президиуме Российской академии наук), г. Москва.
Работа поступила в редакцию 02.03.2015.
Библиографическая ссылка
Евтушенко О.А. ВЛИЯНИЕ ОТЛИЧИЯ РАСПРЕДЕЛЕНИЯ ВНЕШНИХ ПОМЕХ ОТ НОРМАЛЬНОГО НА ЭФФЕКТИВНОСТЬ МЕТОДОВ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ В СРЕДСТВАХ СВЯЗИ, ИСПОЛЬЗУЕМЫХ ПРИ УПРАВЛЕНИИ ВОЗДУШНЫМ ДВИЖЕНИЕМ С АВТОМАТИЧЕСКИМ ЗАВИСИМЫМ НАБЛЮДЕНИЕМ // Фундаментальные исследования. – 2015. – № 4. – С. 67-73;URL: https://fundamental-research.ru/ru/article/view?id=37125 (дата обращения: 23.11.2024).