В сырьевых и перерабатывающих отраслях мировой промышленности для транспортирования и переработки различных сыпучих и кусковых материалов широко применяются вибрационные транспортно-технологические машины (ВТТМ). Самой представительной группой ВТТМ являются виброгрохоты. Традиционные виброгрохоты с дебалансным, кинематическим и электромагнитным приводом имеют невысокие технические и эксплуатационные показатели. Значительная часть вибрационного оборудования, выполняющего данные технологические операции, требует больших затрат энергии. Кроме того, имеется ряд проблем с самой обработкой материалов. Например, разделение и сортировка труднопросеиваемых материалов, самоочистка сит, дезинтеграция агломератов.
Большинство вибрационных машин работают в режиме вынужденных колебаний с зарезонансной настройкой. Резонансные режимы работы машин, являющиеся энергетически наиболее эффективными, практически нереализуемы из-за их низкой стабильности при обычном резонансе вынужденных колебаний. Это объясняется крутизной амплитудно-частотной характеристики и малой величиной резонансной зоны. Поэтому даже небольшие изменения технологической нагрузки выводят машину из резонансного режима.
Положительные результаты по стабилизации резонансного режима удалось получить на основе использования комбинационного параметрического резонанса [1–4].
Целью данной работы является исследование динамики вибрационного грохота, принцип действия которой основан на самовозбуждении многократного комбинационного параметрического резонанса.
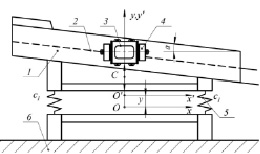
Ключевой особенностью вибрационного грохота на многократном комбинационном параметрическом резонансе является использование параметрического вибровозбудителя, предложенного В.И. Антиповым. Он выступает в роли инновационного вибропривода для возбуждения и поддержания резонансных колебаний грохота. Основным узлом параметрического резонансного вибровозбудителя является роторно-маятниковая система, маятники которой совершают колебательное движение в поле центробежных сил инерции. Маятники этой системы образуют инерционный элемент (ИЭ) вибровозбудителя. На рис. 1 приведена динамическая модель вибрационного грохота. При рассмотрении динамики грохота вводится предположение, что отношение массы технологической нагрузки к массе рабочего органа менее значения 0,2–0,3. В этом случае влияние технологической нагрузки можно учесть путем введения так называемой присоединительной массы.
Ротор ИЭ 4 массой m0 этой системы состоит из набора отдельных одинаковых уравновешенных дисков 7 (рис. 1, б). В каждом диске образована пара незамкнутых беговых дорожек 9 кругового профиля, которые расположены симметрично относительно двух взаимно перпендикулярных его диаметров, а их центры смещены от оси вращения ротора в диаметрально противоположных направлениях на одинаковые расстояния AB = l. На беговых дорожках размещены одинаковые маятники 8 массой m каждый с возможностью обкатки. Диски соединяются между собой в единую конструкцию так, что беговые дорожки одной пары повернуты вокруг оси ротора на угол γ0 = π/s относительно другой, где s – число дисков (s = 2). Ротор ИЭ содержит N = 2s тел качения (маятников), расположенных попарно в параллельных плоскостях [2].
Вибровозбудитель 3 жестко закрепляется на корпусе грохота 1 массой M0. Грохот связан упругими элементами 5 с основанием, которое жестко закреплено на фундаменте 6.
Два одинаковых вибровозбудителя с параллельно расположенными валами, вращающимися в противоположных направлениях с одинаковой угловой скоростью, установлены на коробе грохота так, что их суммарная вынуждающая сила проходит через центр масс грохота. Согласованная работа двух вибровозбудителей на одном рабочем органе достигается благодаря обобщенному принципу самосинхронизации [4]. Используется однонаправленная упругая система, т.е. перемещение в направлении x ≡ 0.
Система координат Ax′y′z′ с началом в центре масс ротора ИЭ движется поступательно относительно неподвижной системы Oxyz.
При равномерном вращении ротора ИЭ тела качения образуют в поле центробежных сил инерции подсистему N маятников с осями обкатки в центрах кривизны беговых дорожек. Положение беговых дорожек определяется углами 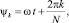 а положение маятников определяется углами φk, k = 1, 2, …, N. Предполагается, что выполнены условия, при которых осцилляторы качения колеблются без скольжения и отрыва, полученные в [5].
а положение маятников определяется углами φk, k = 1, 2, …, N. Предполагается, что выполнены условия, при которых осцилляторы качения колеблются без скольжения и отрыва, полученные в [5].
Примем параметры y, φk, где y – перемещение рабочего органа грохота, за обобщенные координаты системы.
Будем исходить из дифференциальных уравнений движения, полученных в [2], учитывая, что x ≡ 0. Если ввести безразмерное время τ = λ2t, безразмерную координату 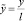 и удержать в указанных уравнениях величины до третьего порядка относительно координат и их производных, то математическую модель вибрационного грохота можно записать в следующем виде:
и удержать в указанных уравнениях величины до третьего порядка относительно координат и их производных, то математическую модель вибрационного грохота можно записать в следующем виде:
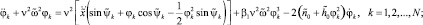
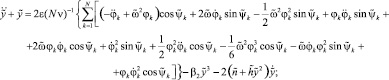 (1)
(1)
где 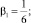
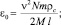
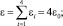
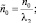
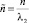 – безразмерные коэффициенты линейного демпфирования;
– безразмерные коэффициенты линейного демпфирования; 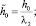
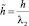 – безразмерные коэффициенты нелинейного демпфирования; β2 = γl2 – коэффициент нелинейности упругих восстанавливающих сил;
– безразмерные коэффициенты нелинейного демпфирования; β2 = γl2 – коэффициент нелинейности упругих восстанавливающих сил; 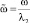 – безразмерная частота параметрического возбуждения;
– безразмерная частота параметрического возбуждения; 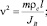 ρc = BCk,
ρc = BCk, 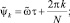
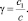 Здесь
Здесь 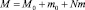 – общая масса системы; JB – момент инерции тела качения относительно оси обкатки;
– общая масса системы; JB – момент инерции тела качения относительно оси обкатки; 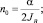

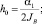
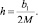 Точка обозначает дифференцирование по τ.
Точка обозначает дифференцирование по τ.
Исследуем комбинационный параметрический резонанс, когда колебания в системе (1) возбуждаются на частотах ω1 и ω2, связанных с частотой параметрического возбуждения  соотношением
соотношением
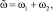 (2)
(2)
причем частоты генерации близки к собственным частотам, т.е. 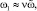 ω2 ≈ 1, и не кратны между собой. Решение уравнений (1) будем искать в виде
ω2 ≈ 1, и не кратны между собой. Решение уравнений (1) будем искать в виде
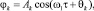 k = 1, 2, …, N,
k = 1, 2, …, N,
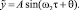 (3)
(3)
Считая амплитуды Ak, A и фазы θk, θ медленно меняющимися величинами и применяя метод усреднения [6], получим следующую систему уравнений первого приближения:
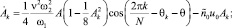
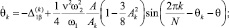 (4)
(4)
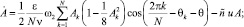
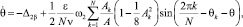 k = 1, 2, …, N,
k = 1, 2, …, N,
где 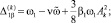
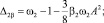
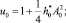
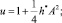
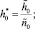
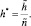 Величины
Величины 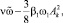
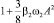 можно рассматривать как парциальные частоты, смещенные за счет нелинейности системы.
можно рассматривать как парциальные частоты, смещенные за счет нелинейности системы.
 а
а 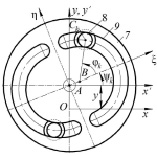 б
б
Рис. 1. Динамическая модель вибрационного грохота
Стационарный режим работы грохота находим из условия 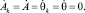 Это приводит к системе алгебраических нелинейных уравнений относительно амплитуд Ak, A и фаз θk, θ. Поскольку осцилляторы качения идентичны, то Ak = A0, k = 1, 2, …, N. Исходя из симметрии роторно-маятниковой системы, указанные уравнения разрешались при выполнении условий
Это приводит к системе алгебраических нелинейных уравнений относительно амплитуд Ak, A и фаз θk, θ. Поскольку осцилляторы качения идентичны, то Ak = A0, k = 1, 2, …, N. Исходя из симметрии роторно-маятниковой системы, указанные уравнения разрешались при выполнении условий
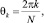 k = 1, 2, …, N. (5)
k = 1, 2, …, N. (5)
В результате приходим к следующим уравнениям:
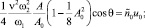
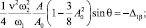
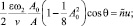
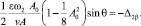 (6)
(6)
Для определения пяти неизвестных величин: двух амплитуд A0, A, двух частот ω1 и ω2, фазы θ, ‒ следует к четырем уравнениям (6) добавить равенство (2). Из первого и третьего уравнений (6) найдем отношение амплитуд
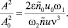 (7)
(7)
Из уравнений (6) можно также определить tgθ и соотношение между расстройками:
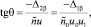 (8)
(8)
где 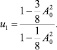
Исключив из уравнений (6) фазовый угол θ и приняв в качестве расстройки величину 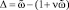 , т.е. расстройку частоты параметрического возбуждения относительно суммы собственных частот, и используя соотношение (7), а также равенство (2), которое теперь принимает вид
, т.е. расстройку частоты параметрического возбуждения относительно суммы собственных частот, и используя соотношение (7), а также равенство (2), которое теперь принимает вид 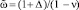 , после некоторых преобразований получим уравнение
, после некоторых преобразований получим уравнение
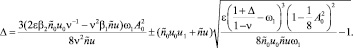 (9)
(9)
Воспользовавшись соотношениями (8), (2) и (7), приходим к уравнению
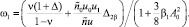 (10)
(10)
 а
а 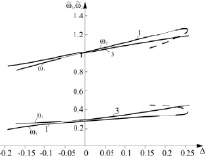 б
б
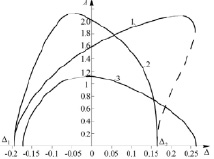
Рис. 2. Резонансные кривые и частоты генерации
Уравнения (9) и (10) позволяют численными методами определить зависимости A(Δ), ω1(Δ) и ω2(Δ). Так как величины u0, u содержат 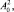 A2, то соотношение (7) приводит к биквадратному уравнению относительно A. Это уравнение имеет решение
A2, то соотношение (7) приводит к биквадратному уравнению относительно A. Это уравнение имеет решение
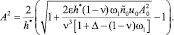
Из (9) следует условие существования стационарных колебаний, которое с учетом соотношения
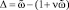
принимает вид
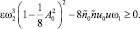 (11)
(11)
Неравенство (11) удовлетворяется тогда, когда при линейном демпфировании выполняется пороговое условие 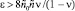 [3] и когда амплитуды A0, A не превышают своих максимальных значений.
[3] и когда амплитуды A0, A не превышают своих максимальных значений.
Результаты численного моделирования уравнений (9) и (10) методом итераций представлены на рис. 2, а, б в виде зависимостей амплитуды A и частот генерации ω1, ω2 от расстройки Δ. На рис. 2, а кривая 1 соответствует комбинационному резонансу, когда
ε = 0,02, n = 0,25, 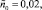
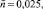
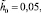
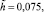
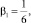 β2 = 0,15.
β2 = 0,15.
Резонансная кривая 2 соответствует случаю, когда β2 = 0, 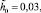
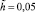 при неизменных значениях остальных параметров. Резонансная кривая 3 построена для величин
при неизменных значениях остальных параметров. Резонансная кривая 3 построена для величин
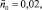
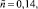
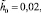
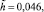 β2 = 0
β2 = 0
и одинаковых значений других параметров.
Отметим свойства параметрических колебаний на примере амплитудной кривой 1. Внутри интервала Δ1 < Δ < Δ2, где Δ1, Δ2 граничные точки области неустойчивости системы (1), состояние равновесия неустойчиво [4]. Граничные точки Δ1 = –0,192, Δ2 = 0,163 определяются из уравнений (7) и (8) при A0 = A = 0. Можно показать, что верхняя ветвь резонансной кривой 1, изображенной сплошной линией, является асимптотически устойчивой, а нижняя (штриховая) – неустойчивой. В точках резонансной кривой, отмеченных тонкой линией, процесс итераций расходится. Точка ∆ = ∆1 является точкой бифуркации, при переходе которой положение равновесия теряет устойчивость и возникает неравновесное состояние – периодические колебания.
Из рис. 2, а следует, что резонансные кривые не имеют характерного максимума, присущего колебательным системам при резонансе вынужденных колебаний. Обнаруживается эффект расширения резонансной зоны. Многократный комбинационный резонанс самовозбуждается в области неустойчивости положения равновесия системы при любых начальных условиях, кроме нулевых, что обеспечивает практически абсолютную устойчивость резонансного режима колебаний.
Определим КПД грохота. Для этого воспользуемся теоремой Мэнли-Роу, применимость которой была доказана в работе [1]. Мощность, рассеиваемая в колебательной системе машины:
P12 = P1 + P2,
где 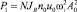 – мощность, потребляемая маятниками ИЭ (управляющей подсистемой) на частоте ω1;
– мощность, потребляемая маятниками ИЭ (управляющей подсистемой) на частоте ω1; 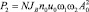 – мощность, расходуемая на выполнение рабочего процесса (полезная мощность). Отсюда КПД машины
– мощность, расходуемая на выполнение рабочего процесса (полезная мощность). Отсюда КПД машины
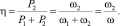 (12)
(12)
При настройке ν = 0,25 и после подстановки ω2 = ω(1 – ν) в выражение (13) получаем η = 0,75. Для сравнения отметим, что максимальный КПД резонансных вибрационных машин в режиме вынужденных колебаний не превышает η = 0,5.
Заключение
Применение параметрических резонансных вибровозбудителей позволяет стабилизировать резонансный режим работы, значительно снизить энергопотребление, а также получать высокие качественные и количественные характеристики вибрационного грохота.
Рецензенты:
Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Кретинин О.В., д.т.н., кафедра «Автоматизация машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Работа поступила в редакцию 16.02.2015.
Библиографическая ссылка
Денцов Н.Н. ДИНАМИКА ВИБРАЦИОННОГО ГРОХОТА НА МНОГОКРАТНОМ КОМБИНАЦИОННОМ ПАРАМЕТРИЧЕСКОМ РЕЗОНАНСЕ // Фундаментальные исследования. 2015. № 4. С. 55-60;URL: https://fundamental-research.ru/ru/article/view?id=37123 (дата обращения: 11.02.2026).



