Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Горбунов М.А. 1 Медведев А.В. 1 Победаш П.Н. 1 Смольянинов А.В. 1

---

1 ФГБОУ ВПО «Московский государственный университет экономики статистики и информатики» Кемеровский филиал

В статье приводится описание финансово-аналитического программного продукта, в основе которого лежит решение линейной задачи оптимального управления в дискретном времени. Кратко изложена концепция моделирования экономических процессов и математический инструментарий для решения задач указанного класса в целях бизнес-планирования. Описана технология построения информационных услуг, а также режимы работы автоматизированного программного комплекса. Приводится краткая характеристика этих режимов и описываются конкурентные преимущества пакета с точки зрения занесения и обработки информации в режиме конструктора моделей и автоматизированного рабочего места бизнес-аналитика. Рассмотрен ряд приложений пакета для решения задач бизнес-планирования как на микро-, так и на мезоэкономическом уровне в аспектах анализа инвестиционных проектов и финансово-хозяйственной деятельности, что в совокупности понимается как стратегическое бизнес-планирование. Подчеркивается необходимость использования именно оптимизационных подходов к моделированию и оценке эффективности стратегического бизнес-планирования.

Статья в формате PDF

707 KB

пакет финансового анализа

технология построения информационных услуг

бизнес-планирование

инвестиционный проект

модель оптимального управления

1. Горбунов М.А. Инструменты диверсификации деятельности организации / М.А. Горбунов, А.В. Медведев // Фундаментальные исследования. – 2014. – № 12(5). – С. 1012–1016.

2. Графический анализатор математических функций и решений алгебраических соотношений с параметрами / Программа для ЭВМ. Свидетельство Роспатента № 2004611968 от 26.08.2004. Правообладатели: А.В. Медведев, А.В. Смольянинов.

3. Гурман В.И., Матвеев Г.А., Трушкова Е.А. Социо-эколого-экономическая модель региона в параллельных вычислениях // Управление большими системами: сборник трудов. – 2011. – № 32. – С. 109–130.

4. Конструктор и решатель дискретных задач оптимального управления («Карма») / Программа для ЭВМ. Свидетельство Роспатента № 2008614387 от 11.09.2008. Правообладатели: А.В. Медведев, П.Н. Победаш, А.В. Смольянинов, М.А. Горбунов.

5. Косинский П.Д., Медведев А.В., Меркурьев В.В., Победаш П.Н. Математическое моделирование агломерации муниципальных образований // Фундаментальные исследования. – 2013. – № 8(6). – С. 1446–1449.

6. Медведев А.В. Концепция оптимизационно-имитационного бизнес-планирования // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 1. – Ч. 2. – С. 198–201.

7. Медведев А.В. Об эффективном инструментарии анализа экономических систем // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 11(5). – С. 763–766.

8. Медведев А.В. Поддержка принятия решений при управлении региональной налоговой политикой // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 4. – С. 25–28.

9. Медведев А.В. Поддержка принятия решений при управлении экономикой региона. монография. – Кемерово: КемГУ, 2011. – 106 c.

10. Медведев А.В., Победаш П.Н. Применение z-преобразования и дискретного принципа максимума к анализу модели реальных инвестиций // Вестник СибГАУ. – 2006. – № 4(11). – С. 32–37.

11. Медведев А.В. Математическая модель оценки инвестиционной привлекательности региона // Современные наукоемкие технологии. – 2013. – № 8–2. – С. 357–361.

12. Медведев А.В. Применение z-преобразования к исследованию многокритериальных линейных моделей регионального экономического развития. монография. – Красноярск: Изд-во СибГАУ имени академика М.Ф. Решетнева. – 2008. – 228 с.

13. Программа для решения многошаговой задачи линейного программирования («Линейная динамика») / Программа для ЭВМ. Свидетельство Роспатента № 2004611491 от 17.06.2004. Правообладатели: А.В. Медведев, П.Н. Победаш.

14. Трусов А.Н., Иванченко П.Ю., Кацуро Д.А. Разработка автоматизированной информационной системы для оптимизационного анализа экономических процессов // Современные наукоемкие технологии. – 2014. – № 11. – С. 38–40.

15. Pobedash P.N. Applications of Operational Approach to Evaluation of Projects of Economic Systems Development // Journal of Siberian Federal University. Mathematics & Physics. – 2013. – № 6(4). – Р. 495–505.

В условиях рыночной экономики предприниматели и бизнесмены сталкиваются с проблемами определения приоритетов развития своего бизнеса, поиска и оценки эффективности распределения ресурсов для обеспечения такого развития и в первую очередь инвестиционного ресурса. Решение указанных проблем в настоящее время практически невозможно без применения автоматизированных программных средств обработки бизнес-информации.

Современные российские (Project Expert, Альт-Инвест, ИНЭК-Аналитик и др.) и зарубежные (SAP R/3, COMFAR и др.) программные продукты, ориентированные на бизнес-планирование, включающие модули планирования ресурсов предприятия (ERP-приложения), управления бизнес-процессами (BPM-приложения) и другие, базируются [6] на использовании преимущественно имитационных моделей описания комплекса бизнес-процессов, то есть не являются задачами оптимального управления. Это не позволяет находить объемы инвестиций, производства продукции и соответствующие показатели финансово-хозяйственной деятельности, выявляющие наилучшие (в смысле выбранных критериев) варианты реализации бизнес-процессов с точки зрения решения задач планирования инвестиционной, производственной, финансовой деятельности (бизнес-планирования). С другой стороны, имеющиеся оптимизационные пакеты либо излишне идеализируют деятельность предприятия, описывая ее производственными функциями абстрактно-математического характера, либо (например, [3]) труднодоступны и громоздки в использовании, что зачастую не удовлетворяет целевую аудиторию конечных пользователей данных пакетов (предпринимателей, бизнес-аналитиков, экономистов).

В этой связи для решения указанных задач бизнес-планирования, на наш взгляд, целесообразно ориентироваться на комбинацию имитационных и оптимизационных методов [1], разрабатывая оптимизационные пакеты финансового анализа, основанные на моделях предприятия, использующих универсальные бухгалтерские алгоритмы и учитывающих юридические особенности, принятые в Российской Федерации при расчете доходных и расходных составляющих финансовых потоков производителя. Указанным требованиям, на наш взгляд, удовлетворяет разработанный авторами программный продукт [4]. В данной работе кратко описывается лежащее в его основе математическое и программное обеспечение поддержки принятия оптимальных решений.

Рассмотрим задачу бизнес-планирования в форме многокритериальной, многошаговой задачи линейного программирования (ММЗЛП) вида

x(t + 1) = A(t)x(t) + B(t)u(t); x(t) = a;

C(t)x(t) + D(t)u(t) ≤ h(t);

u(t) ≥ 0 (t = 0, …, T–1); (1)

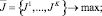
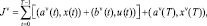
где u(t) = [ul(t)] и x(t) = [xi(t)] – соответственно управляющий и фазовый векторы; A(t) = [aij(t)]; B(t) = [bil(t)]; C(t) = [ckj(t)]; D(t) = [dik(t)] матрицы; a, aν(t) = [ai(t)]ν; bν(t) = [bl(t)]ν; s(t) = [si(t)]; h(t) = [hk(t)] – векторы; (i,j = 1,…,n; l = 1,…,rt; k = 1,…,m; t = 0, …, T; ν = 1, …, K); Jν – ν-й целевой критерий (ν = 1, …, K); K – количество критериев; rt, m, T – размерность управляющего вектора, число ограничений и временных шагов соответственно; (α₀,β₀) – скалярное произведение векторов α₀, β₀; n – количество видов продукции.

Переменные u(t) и x(t), а также элементы матриц и векторов уравнений движения, ограничений и целевых критериев подробно описаны в работе [10]. В работе [7] приведен содержательный смысл используемых в (1) переменных.

В экономических системах справедлив закон временной стоимости денежных потоков, гласящий, что любой сегодняшний финансовый поток обесценивается с течением времени. Для задачи (1) указанный закон может быть смоделирован применением операции дисконтирования целевых критериев:

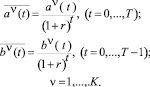(2)

Учитывая особенность коэффициентов целевых критериев, содержащих дисконтирующие множители, с помощью z-преобразования [12] или zT-преобразования [15] от анализа задачи (1) можно перейти к исследованию ее статических аналогов (z- или zT-задач) меньшей размерности:

A_L×2n·X_2n×1(z) ≤ b_L×1, (k = 1, ..., K) (3)

A_L×2n·X_2n×1(z_Т) ≤ b_L×1, (k = 1, ..., K), (4)

где L – количество ограничений, описывающих конкретный вид производственной деятельности; b_L×1 – вектор-столбец правых частей ограничений; c_1×2n – вектор-строка коэффициентов целевой функции; A_L×2n – матрица коэффициентов ограничений.

Оптимальные решения построенных таким образом задач вида (3), (4) сохраняют [12] некоторые важные свойства решений исходной задачи (1), а сами задачи могут быть теоретически исследованы и численно решены (например, на основе вариантов симплекс-метода Дж. Данцига) при практически значимых размерностях, определяемых количеством видов продукции и содержательных ограничений (в авторских расчетах значения n достигали нескольких десятков) в моделируемых бизнес-процессах.

Технология построения информационных услуг

На основе описанного выше математического инструментария разработан комплекс прикладных программ [4, 13], представляющий собой совокупность автоматизированной информационной системы внесения, обработки и анализа входной информации, решателя и многопараметрического графоанализатора решений одно- и многокритериальных задач линейного программирования (МЗЛП). Пакет [4] ориентирован на различных пользователей. Специалисту-математику он позволяет создавать и корректировать математические модели в форме МЗЛП, а также контролировать корректность внесения информации. Экономисту-аналитику, бизнесмену – в удобном режиме создавать собственную конфигурацию бизнес-проекта (выделяя блоки характеристик активов, продукции, внешнего окружения проекта, финансовый блок и т.п.) и заносить входную статистическую и экспертную информацию. А обоим вместе – представлять результаты расчетов как в виде графиков многопараметрических зависимостей, так и в виде Парето-множеств в критериальном пространстве (двух или трех критериев). Пакет [4] предусматривает два режима работы –

1) конструктор моделей;

2) автоматизированное рабочее место аналитика, краткое описание которых приводится далее.

Конструктор моделей

При решении как много-, так и одношаговых задач оптимального управления вида (1) или (3) часто бывает затруднено занесение матричной информации, в первую очередь из-за большого количества или значительной размерности исходных матриц и, как следствие, отсутствия наглядности занесенной информации. Конструктор моделей позволяет создавать пользовательские модели в визуальном режиме, поблочно формируя указанные матрицы. При этом пользователь имеет возможность редактировать векторно-матричную информацию, имея перед глазами как образ всей матрицы, так и ее произвольных блоков (как показано на рис. 1, где представлен типичный скриншот конструктора моделей).

Кроме того, в пакете также имеется отладчик, позволяющий обнаруживать ошибки или противоречия в занесенной числовой информации) в занесении числовой информации модели (рис. 2).

Автоматизированное рабочее место (АРМ) бизнес-аналитика

В этом режиме исследователь после внесения числовой информации из предметной области на выходе получает результаты расчета, а также возможности их графического анализа. Данный режим работы предъявляет минимальные требования к подготовке пользователя – владение информацией о содержательном смысле числовых параметров модели, – предоставляя возможность легко освоить работу с пакетом студентам или специалистам с относительно небольшим набором знаний в предметной области. Пример окна интерфейса работы пакета в описываемом режиме приведен на рис. 3.

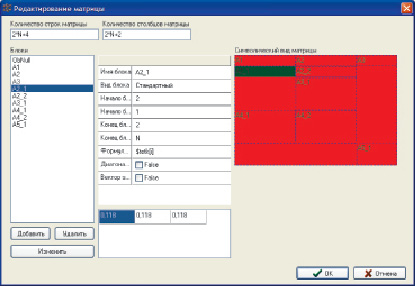
Рис. 1. Визуальный редактор матриц

Пакет [4] позволяет построить большое количество графиков зависимостей показателя эффективности бизнес-проекта от параметров модели с возможностью выбора шага расчетов в широком диапазоне изменения значений параметров. Кроме того, на одном рисунке можно проводить параметрический анализ графиков, меняя значения параметров в соответствующих окнах интерфейса (слева на рис. 3). Пакет предусматривает также построение двух- и трехмерных Парето-множеств (в пространстве критериев) при решении многокритериальных задач.

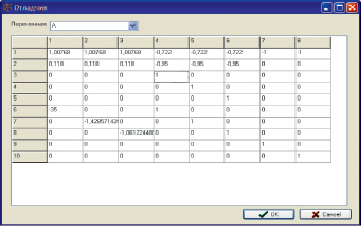
Рис. 2. Отладчик матриц

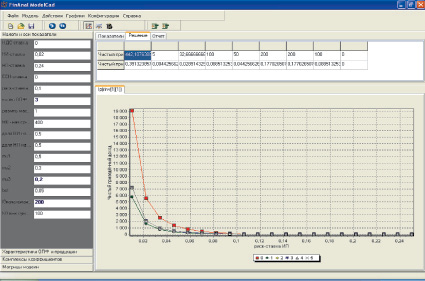
Рис. 3. Окно интерфейса АРМ бизнес-аналитика

К основным преимуществам созданного программного обеспечения, на наш взгляд, относятся:

• возможность создания математической модели в пользовательском режиме;
• наличие анализатора математических формул;
• визуальный редактор матриц, задаваемых поблочно, позволяющий заполнять их по заданным формулам, с помощью анализатора формул;
• возможность разделения параметров модели по группам для создания собственной конфигурации проекта;
• возможность защиты данных модели от несанкционированного доступа;
• возможность добавления описания модели;
• высокая скорость расчетов (график, содержащий информацию, получаемую при последовательном решении 100 задач линейного программирования, строится не более чем за 1 секунду);
• поддержка возможности выбора различных математических решателей с учетом математической модели, описывающей бизнес-проект. Например, библиотека с реализацией одно- или двухфазного симплекс-метода и библиотека с реализацией решателя с помощью генетических алгоритмов и пр.);
• встроенная система шифрования Blowfish;
• интуитивно понятный пользовательский интерфейс;
• построение и параметрический анализ большого количества графиков зависимостей от любых параметров модели на одном рисунке, а также параметрический анализ Парето-множеств;
• гибкая настройка вида графиков (легенда, метки, значения в точках);
• использование при вводе-выводе информации оригинального быстродействующего графического анализатора функций [2], позволяющего эффективно обрабатывать многопараметрические функции;
• масштабирование отдельных частей графиков для более детального их анализа.

Таким образом, комплекс программ [4, 13] является для конечного пользователя удобной основой при решении задач бизнес-планирования и получения оптимальных значений объемов инвестиций, производства продукции и соответствующих параметров финансово-хозяйственной деятельности предприятий (потоков прибыли, амортизации, налогов, заемных и собственных средств производителя и пр.). Кроме того, пакет совершенствуется и развивается [14] в направлении интересов конечного пользователя – экономиста, финансиста, организатора бизнеса, управленца регионального уровня, – дополняясь блоками предобработки (автоматизированного внесения информации), а также автоматизированной постобработки полученной при решении информации.

Пакет [4] в настоящее время используется при расчете ряда инвестиционных проектов стратегического планирования в регионе [9, 11], бизнес-проектов малого и среднего бизнеса, оценки эффективности коммерческих проектов, проектов производственного [1], финансового [8] и управленческого [5] содержания.

Рецензенты:

Зыков В.С., д.т.н., профессор, главный научный сотрудник НИИ горной геомеханики и маркшейдерского дела (ОАО «ВНИМИ»), Кемеровское представительство, г. Кемерово;

Косинский П.Д., д.э.н., профессор кафедры государственного и муниципального управления Кузбасского государственного технического университета им. Т.Ф. Горбачева, г. Кемерово.

Работа поступила в редакцию 18.02.2015.

Библиографическая ссылка