Известно [1, 3, 4], что многие ученые в области акустики трактовали реверберационный процесс с качественной точки зрения как процесс нарастания уплотнения совокупности отраженных сигналов, происходящий одновременно с нарастанием времени реверберации. Однако количественные категории этого явления оставались нераскрытыми, т.к. процесс нарастания числа отражений по классической теории не учитывает того обстоятельства, что эти отраженные сигналы доходят до точки приема в разные моменты времени. Процесс же уплотнения должен фиксироваться для тех отраженных сигналов, которые приходят в точку приема единовременно.
В [2] было показано, что модель Эйринга [7] не может рассматриваться как адекватное теоретическое описание реального реверберационного процесса. Критика этой модели в данном контексте основывается не столько на утверждении, что реверберация является главным параметром оценки качества помещения с акустической точки зрения, сколько на анализе динамической структуры самого процесса затухания. В методе описания процесса отражения звукового сигнала в помещении, предложенном Эйрингом, по сути никакой хаотичности не присутствует, потому что отражение происходит одновременно ото всех поверхностей с определенным тактом, как бы в сферическом помещении, что не соответствует реальному процессу. Тактовость процесса может нейтрализоваться при числе отражений, близком к бесконечности. В реальности же подобное длительное время наблюдения в практике измерений никогда не достигается.
В той части реверберационного сигнала, которую мы рассматриваем как воспринимаемый слухом переходной процесс, фактическая слуховая оценка связана лишь с начальной частью, которая не удовлетворяет условию эргодичности. И более того, поскольку все отражения происходят одновременно, на процесс отражения накладывается определенный такт, которого на самом деле нет. В результате получается, что положение модели об одновременности всех отражений не является корректным.
Второе положение, которое вызывает сомнение в рамках традиционной теории реверберации, это постоянство количества отраженных от ограничивающих поверхностей помещения сигналов. Более общая теория реверберации, разработанная Шустером и Вейцманном [8], утверждает, что предшествовавшие теории описывают только путь прохождения одиночного звукового луча в помещении и что при отражении сигнала энергия падающего сигнала распределяется между отраженными. Согласно принципу Гюйгенса [5], каждая точка фронта (поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени. Т.е. в процессе отражения от поверхности звука сама поверхность становится новым источником с энергией, равной разности между пришедшей к поверхности энергией и поглощенной самой поверхностью. Таким образом, можно показать, что количество сигналов при каждом акте отражения увеличивается.
Модификация существующей модели реверберационного процесса
Для создания адекватной математической модели необходимо установить структуру сигнала в данной точке наблюдения. Структура должна быть дискретной с точки зрения отдельных сигналов отражения. Как правило, под дискретными сигналами подразумеваются сигналы бесконечно короткой длительности с детерминированной амплитудой. В данном случае такое представление сигнала возможно лишь при использовании в качестве возбуждающего систему «звук ‒ помещение» сигнала дельта-импульса. Как правило, для изучения акустических характеристик помещения такие импульсы используют, имитируя характеристики дельта-импульса выстрелами из стартового пистолета, лопанием воздушных шаров и прочее. В случае использования системы звукоусиления возможно использовать записанные ранее и воспроизведенные через эту систему звуковые сигналы. Использование подобных сигналов в анализе процесса переотражения звука в помещении позволяет достаточно четко обнаружить начало и конец акустического сигнала, пришедшего в точку наблюдения. Это возможно сделать при достаточно высоком разрешении регистрирующих и анализирующих приборов, в качестве которых в настоящее время могут быть использованы персональные компьютеры, оборудованные точными аналого-цифровыми и цифро-аналоговыми преобразователями.
При построении адекватной структуры реверберационного сигнала необходимо иметь в виду также упускаемый Эйрингом аспект перераспределения энергии звукового сигнала в процессе отражения его от ограждающей поверхности. В результате этого отражения, даже если пренебречь потерей энергии при поглощении элементами акустической обработки помещения и прохождением сигнала сквозь ограждающую поверхность, энергия исходного падающего сигнала перераспределится между отраженными сигналами.
Моделирование по модифицированному методу
При моделировании процесса накопления отражений и установления их плотности для большей наглядности рассмотрим процесс переотражения звука на двухмерной модели. При необходимости методику можно экстраполировать на трехмерную модель введением поправки на высоту размещения мнимого источника относительно микрофона. Помещение будет обладать следующими геометрическими размерами: высота h = 10 м, ширина b = 14,5 м, длина l = 21 м.
На рис. 1 показан фрагмент плана помещения для расчета сигналов от мнимых источников. Он включает в себя, помимо непосредственно основного помещения и мнимых источников, расположенных в поясах отражений [6], концентрические окружности, отстоящие пространственно друг от друга на расстояние средней длины свободного пробега звука в данном помещении. Из формулы среднего времени пробега [4]
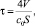 (1)
(1)
где V – объем исследуемого помещения; c0 – скорость звука при нормальных условиях; S – суммарная площадь ограничивающих поверхностей, можно получить среднюю длину пробега l0:
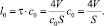 (2)
(2)
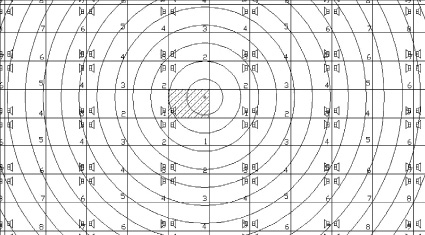
Рис. 1. Фрагмент плана исследуемого помещения для расчета плотности отражений методом мнимых источников
В случае помещения с вышеуказанными параметрами среднее время пробега в помещении τ0 = 26,9 мс, средняя длина пробега l0 = 9,23 метра. Вычерчивая концентрические окружности с шагом, равным средней длине пробега в помещении, получаем возможность установить, какие отражения будут приходить в один и тот же временной интервал, т.к. все точки, находящиеся внутри кольца, ограниченного двумя концентрическими окружностями, будут отстоять от центра на одно и то же расстояние, ограниченное средней длиной пробега. Центром же данных окружностей следует взять точку наблюдения. Таким образом, вычертив достаточное количество концентрических окружностей с равным шагом, можно пронаблюдать поведение отражений внутри заданного интервала в разные моменты времени. Условием достаточности можно считать утверждение, что ранними отражениями считаются отражения, пришедшие в интервал от начала процесса до 50‒80 мс в зависимости от рассматриваемого звукового материала [1]. Если при этом рассчитать номер мнимого помещения для каждого мнимого источника, то становится возможным установить число пересечения поверхностей данного помещения звуковым сигналом из данного мнимого источника. Знание этого числа дает возможность рассчитать суммарные потери энергии, что, в свою очередь, позволяет рассчитать суммарный вклад всех отражений в энергию внутри наблюдаемого интервала.
Для подсчета количества отражений в течение среднего времени свободного пробега для каждого отражения нужно установить номер, вычислить остаточную энергию по формуле, вывод и обоснование которой приведены в [2]:
E(t) = E(1 – α)n. (3)
Складывая эти значения, безотносительно исходной энергии источника, можно установить характер поведения энергии звукового сигнала в течение наблюдаемого интервала. Результат сложения проиллюстрирован на графике (рис. 2). По оси абсцисс идет отсчет номера интервала наблюдения, по оси ординат – количество отражений, существующих внутри этого интервала.
В этом случае, как видно из рисунка, мы можем определить количество сигналов, приходящих в центр данной окружности в один и тот же момент времени. Если мы хотим определить количество сигналов, приходящих в другую точку пространственного расположения приемника, мы должны поменять центр этих окружностей и проделать ту же процедуру.
Для проверки этого утверждения построим подобный план для помещения, в котором приемник звука будет находиться на более близком расстоянии от источника, чем в первом варианте. Данное положение проиллюстрировано на рис. 3.
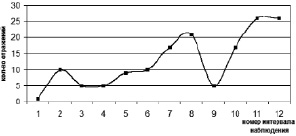
Рис. 2. Изменение количества отраженных сигналов с увеличением времени наблюдения

Рис. 3. Фрагмент плана исследуемого помещения для расчета плотности отражений методом мнимых источников для второго варианта расположения
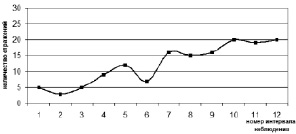
Рис. 4. Изменение количества отраженных сигналов с увеличением времени наблюдения при изменении положения приемника
При изменении положения приемника изменяется количество мнимых источников звука, сигналы от которых приходят в один и тот же установленный выше интервал времени. Одновременно из-за изменения координат приемника, так как концентрические окружности изменяют свое положение относительно мнимых источников, мнимые источники могут перемещаться из одного кольца наблюдения в другое.
Это приводит к перераспределению сигналов, приходящих в один интервал времени, что, в свою очередь, приводит к изменению и их количества. Данное утверждение проиллюстрировано на рис. 4.
Заключение
Как можно видеть, в обоих промоделированных случаях в течение времени наблюдения количество одновременно существующих сигналов отражения увеличивается, что подтверждает постулат, указанный в [2] и приведенный к рассмотрению в данной статье. Также можно наблюдать, что количество существующих в течение одинакового интервала наблюдения отражений не остается постоянным для разных точек наблюдения. Данный аспект позволяет обосновать факт неоднородности звукового поля в процессе переотражения сигнала, и, следовательно, картины реверберационной кривой. Эта неоднородность будет проявляться в изменении характера поведения кривой в зависимости от точки наблюдения.
Приведенный анализ влияния взаимного расположения источника звука и приемника показывает неодинаковость реверберационной кривой в различных точках помещения. Следует отметить, что мы интересуемся причиной неодинаковости измеренного времени реверберации в разных координатных точках помещения и объясняем эту неравномерность (в рамках классического объяснения) интерференционными явлениями, возникающими из-за того, что мы можем измерять только потенциальную составляющую энергии, обусловленную звуковым давлением. В действительности неравномерность результатов обусловлена не только интерференционными явлениями, но и тем обстоятельством, что энергия различных участков помещения (мгновенная) неодинакова из-за того, что совокупное расстояние, определяемое по изломанной в результате отражения траектории, в разных местах помещения будет разным. Следовательно, измеренное время реверберации будет неодинаковым не только из-за интерференционного взаимодействия. Рассмотренные в рамках данной статьи утверждения могут быть использованы для увеличения точности расчетов при проектировании помещений с использованием существующей статистическо-геометрической теории реверберации.
Рецензенты:
Майзель А.Б., д.т.н., профессор, начальник отдела, ОАО «ЦКБ МТ «Рубин», г. Санкт-Петербург;
Уваров В.К., д.т.н., профессор кафедры математики и физики, ФГБОУ ВПО «Санкт-Петербургский государственный институт кино и телевидения», г. Санкт-Петербург.
Работа поступила в редакцию 02.03.2015.
Библиографическая ссылка
Вахитов Я.Ш., Давыдов Д.А. МЕТОД ПОСТРОЕНИЯ МОДЕЛИ РЕВЕРБЕРАЦИИ, АДЕКВАТНОЙ РЕАЛЬНОМУ ПРОЦЕССУ РАСПРОСТРАНЕНИЯ СИГНАЛА // Фундаментальные исследования. 2015. № 4. С. 32-36;URL: https://fundamental-research.ru/ru/article/view?id=37119 (дата обращения: 11.02.2026).



