Задача синтеза системы управления сегодня является актуальной в связи с развитием робототехнических устройств, которые должны выполнять различные задания автономно, без участия человека. Формально задача синтеза управления заключается в нахождении функций, которую часто называют синтезирующей, описывающей зависимость управления от состояния объекта. Найденное с помощью синтезирующей функции управление обеспечивает достижение цели управления и является оптимальным согласно заданному критерию качества. В общем виде аналитического метода решения задачи синтеза управления не существует. В работе для решения задачи синтеза управления применяется метод аналитического программирования.
Аналитическое программирование [10, 11, 12] является разновидностью метода генетического программирования [7, 8, 9]. В настоящей работе метод аналитического программирования применен для решения задачи синтеза системы управления летающим роботом. Проблема управления движением летающего робота по пространственной траектории состоит в обеспечении точного и быстрого движения по заданной точками траектории. При реализации управления возникает дополнительная задача обеспечения проверки условия переключения точек на траектории. В работах [7, 10, 11] для решения задачи синтеза системы управления летающим роботом используется метод сетевого оператора. Проблема переключения точек решается с помощью синтеза логико-функционального управления или синтеза двух контуров управления, состоящих из системы стабилизации объекта относительно точки и логической системы переключения точек. Метод синтеза обусловлен ограниченным набором функций, которые использует метод сетевого оператора, это функции с одним или двумя аргументами. Принципиальную трудность при синтезе интеллектуальных систем управления методом сетевого оператора представляет собой функция, описывающая оператор условия, которая должна иметь три или более аргументов. Метод аналитического программирования может использовать любой набор функций, в том числе с тремя и более аргументами.
Для эффективного применения метода аналитического программирования к решению задачи синтеза управления в работе представлен метод вариационного аналитического программирования [3, 4, 5]. Данный метод позволяет сузить пространство поиска и определить область поиска за счет выбора базисного решения.
Метод вариационного аналитического программирования
Введем упорядоченные множества функций с определёнными количествами аргументов
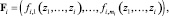
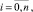 (1)
(1)
где fi,j(z1, ..., zi) – функция под номером j с количеством аргументов i, 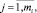
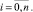
Объединим все множества в одно
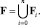 (2)
(2)
Пронумеруем все элементы объединённого множества
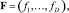 (3)
(3)
где
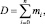 (4)
(4)
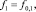
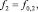 …,
…, 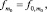
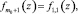 …,
…, 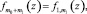
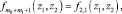 …,
…,
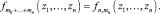
Отдельно рассмотрим множество функций без аргументов или с нулевым количеством аргументов. Данное множество для математических выражений представляет собой множество параметров или переменных
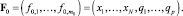 (5)
(5)
Запись кода математического выражения в методе аналитического программирования осуществляется в форме упорядоченного множества целых чисел
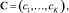 (6)
(6)
где 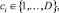
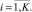
Каждое число указывает на номер элемента в объединенном множестве F (7). Запись имеет префиксный порядок. Код функции в записи предшествует коду аргумента. Длина записи кода ограничена. Дополнительное множество переменных и параметров используется для корректного завершения записи. При необходимости код функции из объединённого множества используется в виде кода для элемента множества переменных или параметров.
Для получения математического выражения из записи кода необходимо знать количества элементов в каждом из множеств функций: m0, ..., mn и количества используемых переменных и параметров N и p.
Количество аргументов функции i и номер функции j определяем по значению элемента ck кода математического выражения с помощью соотношений
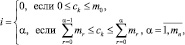 (7)
(7)
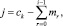 1 < i ≤ n. (8)
1 < i ≤ n. (8)
При соответствии элемента кода ck функции без аргументов, i = 0 для определения переменной xj или параметра qj необходимо использовать количества используемых переменных N и параметров p.
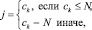 i = 0, (9)
i = 0, (9)
где код ck соответствует переменной xj, если ck ≤ N, или параметру qj, если N < ck ≤ m0.
Для описания кодов векторных математических выражений используем один набор целых чисел с определенным количеством элементов для каждого компонента векторного выражения. Пусть вектор математических выражений имеет M компонент. Выделим под каждую компоненту вектора L позиций в коде записи. Код математического выражения каждого компонента i векторного выражения содержит ki ≤ L элементов, 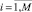 . Не используемым в формировании кода элементам задаем нулевые значения:
. Не используемым в формировании кода элементам задаем нулевые значения:
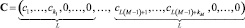 (10)
(10)
где L – число позиций для кода одной компоненты векторного выражения; ki – длина кода компоненты i векторного выражения, 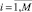 .
.
В коде записи векторного выражения (14) значения для элементов выполняются условия
cj = 0,
если 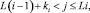
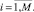 (11)
(11)
Для расшифровки кода векторного выражения необходимо вместе с величинами mi, 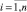 , N и p дополнительно знать число позиций L и длины кодов компонент ki,
, N и p дополнительно знать число позиций L и длины кодов компонент ki, 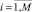 .
.
Для определения корректности записи кода математического выражения используем индекс элемента. Пусть в записи кода (10) математического выражения элемент cj ≠ 0. Для векторного математического выражения определим него номер компоненты i из соотношения
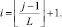 (12)
(12)
Для корректной записи для индекса элемента cj ≠ 0 необходимо выполнение условий
T(j) > 0, j ≠ ki; (13)
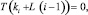 (14)
(14)
где T(j) ‒ индекс элемента j записи кода математического выражения.
Для вычисления индекса T(j) элемента j при условии cj ≠ 0 используем соотношение
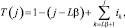 (15)
(15)
где
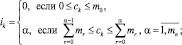 (16)
(16)
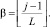 (17)
(17)
Индекс T(j) элемента j указывает на минимальное число недостающих справа элементов. Невыполнение условий (13) или (14) указывает на неправильность записи математического выражения.
Алгоритм для вычисления математического выражения по записи кода в аналитическом программировании должен располагать информацией о максимальном количестве аргументов в используемых функциях.
Метод вариации аналитического программирования
Пусть запись кода (10) определяет пространства записей математических выражений. Пространство всех вариантов возможных записей длины K для D значений кодов содержит DK элементов.
Малой вариацией кода аналитического программирования является изменение значения кода элемента ci Î {1, ..., D}. Одной малой вариации достаточно для получения любой записи пространства из одной заданной записи за конечное число вариаций.
Для описания малой вариации используем вектор из двух компонент
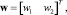 (18)
(18)
где w1 – номер позиции изменяемого кода элемента записи; w2 – значение кода элемента.
Для выполнения вариации необходимо знать: количество элементов в векторном выражении M, количество переменных N, количество параметров p, количество используемых функций определенной арности m0 = N + p, m1, ..., mn, количество выделенных для каждой компоненты позиций L и количество используемых в варьируемом коде позиций ki, 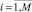 .
.
Номер позиции w1 в векторе вариации (18) не должен превышать количество позиций в коде
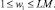 (19)
(19)
Значение кода элемента w2 не должно превышать количество элементов в объединенном множестве (18):
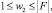 (20)
(20)
где
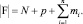 (21)
(21)
Синтез системы управления летающим роботом
Рассмотрим задачу синтеза управления движением летающего робота по пространственной траектории.
Модель объекта управления задана в виде системы обыкновенных дифференциальных уравнений
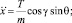 (22)
(22)
 (23)
(23)
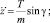 (24)
(24)
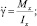 (25)
(25)
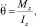 (26)
(26)
где 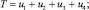
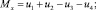
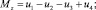 ui – величина силы тяги i-го винта, i = 1, 2, 3, 4; g = 9,81 м/c2; Ix = 0,03 кг∙м2, Iz = 0,03 кгм2, m = 1 кг.
ui – величина силы тяги i-го винта, i = 1, 2, 3, 4; g = 9,81 м/c2; Ix = 0,03 кг∙м2, Iz = 0,03 кгм2, m = 1 кг.
Заданы точки пространственной траектории в виде упорядоченного множества значений векторов из трех компонент:
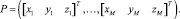 (27)
(27)
В вычислительном эксперименте рассматривалось M = 16 точек траектории
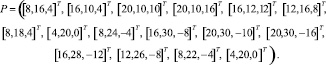
Критерием качества управления являлся функционал
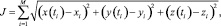 (28)
(28)
где 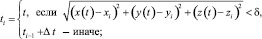 (29)
(29)
Δt = 8 c; δ = 0,25 м; t0 = 0.
Для системы были заданы следующие начальные значения:
x(0) = ±1 м; 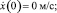 y(0) = 20 ±1 м;
y(0) = 20 ±1 м;
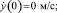 z(0) = 0 м;
z(0) = 0 м; 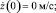
y(0) = 0 рад., 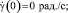 θ(0) = 0 рад.;
θ(0) = 0 рад.; 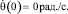
На управление были наложены ограничения
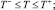
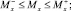
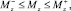 (30)
(30)
где T– = 6 Н; T+ = 16 Н; 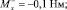

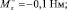
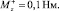
В результате было получено следующее оптимальное управление:
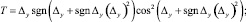
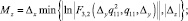 Mx = Δz,
Mx = Δz,
где
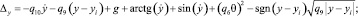
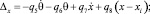
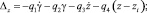
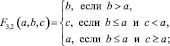
q1 = 1,075; q2 = 3; q3 = 0,527; q4 = 0,324; q5 = 1,075; q6 = 3; q7 = 0,527;
q8 = 0,324; q9 = 15,51; q10 = 15,19; q11 = 1,89.
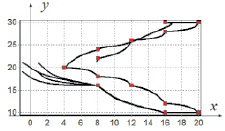
Рис. 1. Движение летающего робота в вертикальной плоскости {x, y}
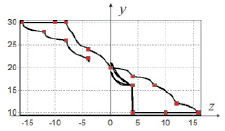
Рис. 2. Движение летающего робота в вертикальной плоскости {y, z}
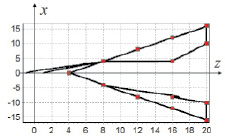
Рис. 3. Движение летающего робота в вертикальной плоскости {x, z}
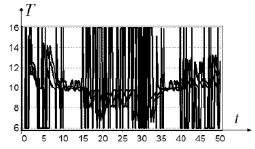
Рис. 4. Управление T для четырех начальных условий
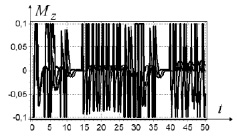
Рис. 5. Управление Mz для четырех начальных условий
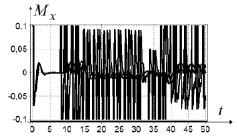
Рис. 6. Управление Mx для четырех начальных условий
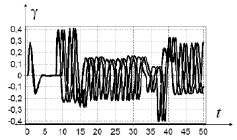
Рис. 7. Угол γ для четырех начальных условий
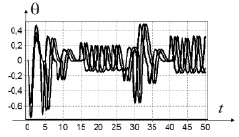
Рис. 8. Угол θ для четырех начальных условий
Траектории движения летающего робота из четырех начальных условий:
1) x(0) = +1 м, y(0) = 21 м;
2) x(0) = –1 м, y(0) = 21 м;
3) x(0) = +1 м, y(0) = 19 м;
4) x(0) = –1 м, y(0) = 19 м; приведены на рис. 1–8.
Заключение
Результаты моделирования показали, что полученная система управления обеспечивает прохождение объекта точно по пространственной траектории. Начальные условия существенно не влияют на точность движения по траектории.
Работа выполнена при финансовой поддержке гранта РФФИ № 14-08-00008-а.
Рецензенты:
Никульчев Е.В., д.т.н., профессор, проректор по научной работе, НОУ ВО «Московский технологический институт», г. Москва;
Логинова Е.Ю., д.т.н., профессор кафедры «Электропоезда и локомотивы», ФГОУ ВПО «Московский государственный университет путей сообщения», г. Москва.
Работа поступила в редакцию 04.02.2015.
Библиографическая ссылка
Дивеев А.И., Конырбаев Н.Б. ПРИМЕНЕНИЕ МЕТОДА ВАРИАЦИОННОГО АНАЛИТИЧЕСКОГО ПРОГРАММИРОВАНИЯ ДЛЯ СИНТЕЗА УПРАВЛЕНИЯ ЛЕТАЮЩИМ РОБОТОМ // Фундаментальные исследования. 2015. № 3. С. 51-57;URL: https://fundamental-research.ru/ru/article/view?id=37083 (дата обращения: 05.03.2026).



